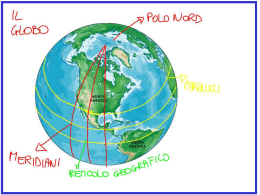
Galileo e la determinazione della
longitudine
Francesco Berrilli
Dipartimento di Fisica
Università di Roma Tor Vergata
Che fai tu, luna, in ciel? dimmi, che fai,
Silenziosa luna?
Sorgi la sera, e vai,
Contemplando i deserti; indi ti posi.
Ancor non sei tu paga
Di riandare i sempiterni calli?
Ancor non prendi a schivo, ancor sei vaga
Di mirar queste valli?
Somiglia alla tua vita
La vita del pastore.
Sorge in sul primo albore
Move la greggia oltre pel campo, e vede
Greggi, fontane ed erbe;
Poi stanco si riposa in su la sera:
Altro mai non ispera.
Dimmi, o luna: a che vale
Al pastor la sua vita,
La vostra vita a voi? dimmi: ove tende
Questo vagar mio breve,
Il tuo corso immortale?
XXIII - CANTO NOTTURNO Dl UN PASTORE ERRANTE DELL' ASIA
indice
•
•
•
•
•
•
•
•
Le stelle, la Terra ed il tempo
Le coordinate terrestri e celesti
Interludio 1: il tempo che respira
Il problema della longitudine
Il telescopio di Galilei e le osservazioni di Giove
L’idea di Galileo
Interludio 2: la luce rallenta e la Francia si restringe
epilogo
Media latitudine Nord che guarda a Sud
Il cammino delle stelle
dall’equatore
Guardando ad Ovest all’equatore
Il cammino delle stelle a Sud
• La rotazione della Terra
rappresenta un preciso orologio,
poiché la lunghezza di un giorno
aumenta solamente di un
secondo ogni 45000 anni.
• Per la determinazione del tempo
per le attività quotidiane è
sufficiente determinare
l'orientazione della Terra per
stabilire l'ora.
• Un sistema pratico utilizzato fin
da tempi remoti è l'osservazione
della posizione del Sole.
• Sfortunatamente però la posizione
del Sole è determinata non solo
dalla rotazione terrestre ma anche
dalla rivoluzione di questa intorno
ad esso.
I sistemi di coordinate sferici
•
•
La posizione di un punto sulla sfera (terrestre o
celeste) è determinata da due coordinate angolari
Per la loro definizione abbiamo bisogno di due piani,
generalmente presi perpendicolari tra loro.
1. Il piano fondamentale F
2. Il piano di riferimento R
•
Le intersezioni di questi due piani con la sfera
saranno dei cerchi massimi detti rispettivamente
cerchio fondamentale e cerchio di riferimento.
Il sistema alto-azimutale
• Si tratta del sistema di riferimento più prossimo alla nostra
esperienza quotidiana.
• Il piano del cerchio fondamentale è quello orizzontale, definito
come il piano perpendicolare alla direzione della verticale
locale (direzione Zenit – Nadir, filo a piombo)
• Il piano del cerchio di riferimento è il piano verticale che
contiene l’asse di rotazione terrestre.
• I due piani intersecano la sfera celeste lungo due cerchi
massimi che si chiamano Cerchio dell’orizzonte e Meridiano del
luogo.
• I cerchi paralleli all’orizzonte si chiamano paralleli di altezza o
almuncantarat. Ogni cerchio massimo generato da piani
appartenenti al fascio di piani che ha come asse la verticale
prende il nome di cerchio verticale.
• Primo verticale è il nome del cerchio verticale passante per i
punti Est ed Ovest, e quindi perpendicolare al piano meridiano.
• Nel sistema h-a le coordinate
sono:
• L’azimut A
• L’altezza h (o la distanza zenitale)
• Per derivare l’azimut si consideri il
meridiano ed il piano verticale
passante per l’astro, l’angolo
formato tra questi due piani
contato da N verso E (o da S
verso O) è l’azimut.
• L’altezza (h) è l’angolo formato tra la direzione dell’astro ed il
piano orizzontale.
• Un astro sarà alla sua culminazione superiore quando transita
al meridiano centrale tra N ed il cerchio orizzonte.
• L'arco complementare dell'altezza si chiama distanza zenitale
ed è rappresentata dall'angolo ZOT dove Z è lo zenit
dell'osservatore. La distanza zenitale si indica generalmente con
z. Risulta quindi:
z = 90°-h
• Nel sistema equatoriale assoluto
le coordinate sono:
• L’ascensione retta (A.R. o )
• La declinazione ()
• Il piano del cerchio origine viene
preso intersecando la sfera con un
piano passante per l’asse di
rotazione del mondo ed il punto
equinoziale di primavera, detto
anche punto  (gamma).
•Il piano del cerchio fondamentale è quello equatoriale
•Per derivare  si misura l’angolo diedro formato dal piano del
cerchio origine e quello del cerchio massimo passante per l’astro
e per i Poli Celesti. Si misura in h, m, s.
•La misura di A.R. può essere ricondotta ad una misura del
tempo, infatti il cerchio meridiano di un luogo in ogni istante (ora
locale) coincide, per costruzione, con un cerchio di A.R.
Polo Nord
Il cammino delle stelle
• L’orizzonte è un piano
tangente.
• Ogni ossservatore, in
ogni momento, può
vedere solo metà del
cielo (o sfera celeste).
• L’orizzonte
astronomico è il piano
tangente alla superficie
della terra.
• Possiamo osservare
come il piano
dell’orizzonte dipende
dalla posizione
dell’osservatore.
Determinazione delle coordinate h-Az
• Step 1 – determinare il circolo verticale
dell’oggetto e calcolare l’azimuth.
Determinazione delle coordinate h-Az
• Step 2 – determinare l’altezza dell’oggetto
Observer in Lincoln (lat = 41 N)
C
A
D
B
Az
Alt
A
0
41 
B
90
0
C
180
49
D
~230 ~45
La polare a
diverse latitudini
Coordinate celesti e coordinate
geografiche
• Step 1: L’altezza
del Polo Nord
Celeste (PNC) è
uguale alla
latitudine
dell’osservatore.
Coordinate celesti e coordinate
geografiche
• Step 1: altezza del
PNC= latitudine
• Step 2: massima altezza
dell’equatore celeste è
pari a 90° - latitudine.
• La longitudine è un
problema molto più
complicato.
Intervalli di
declinazione
3 tipi di stelle
Circumpolari
Sorgono e
tramontano
Non sorgono mai
Regole generali
• Intervallo Circumpolare – da (90 – lat) al
polo (90) nell’emisfero dell’osservatore.
• Non sorgono mai – una regione
simmetrica all’intervallo Circumpolare (90lat) al polo (90) nell’altro emisfero.
• Sorgono e tramontano – tutto il resto – I
tre intervalli coprono ovviamente 180 - da
(90-lat) in un emisfero a (90-lat) nell’altro.
Interludio 1 - il tempo che respira
• Alla domanda “quanto è lunga una settimana?”
rispondiamo in genere 7 giorni, e non ¼ di
mese.
• Tuttavia, sono i cicli lunari (ancora riportati sui
calendari), con i vari quarti, a far sorgere l’idea
di settimana.
• Nell’antico Egitto il tempo era scandito da
episodi importanti, in genere astronomici: i cicli
del Sole, della Luna, le 36 stelle (costellazioni?)
dell’emisfero meridionale (i decani), di Sirio, del
Nilo.
• Venivano solennizzate 12 metamorfosi del
sole nel suo passaggio attraverso il cielo le
quali costituivano oggetto di particolari
meditazioni. Queste corrispondevano a 12
capitoli nel libro dei morti.
Da Il tempio del cosmo, Religione.
Magia e miti nell’Antico Egitto
Neri-Pozza Ed.
• Durante l’anno il numero di ore assegnate
al giorno ed alla notte rimaneva uguale,
dunque le ore del dì dovevano essere
ampliate per l’estate e ridotte per l’inverno.
• Analogamente accadeva per le ore della
notte.
• Il tempo respirava come un organismo.
Il problema della longitudine
• Durante la navigazione in alto mare gli unici punti di
riferimento sono le stelle ed il Sole.
• Per fare il punto nave e tracciare la rotta è necessario
localizzare se stessi su una griglia immaginaria di linee di
latitudine e longitudine.
• I Portoghesi, i primi navigatori che si avventurarono in mare
aperto nel XV secolo, equipaggiarono le proprie navi con
strumenti (astrolabi, balestriglie) per la misura dell’altezza
degli astri al fine di determinare la latitudine.
• La longitudine era un problema molto più complicato.
Sole e stelle non erano di molto aiuto senza una accurata
conoscenza della differenza di tempo locale tra un punto di
origine (per il quale ad esempio erano calcolate le
effemeridi) ed il punto in cui ci si trovava.
Già nel secolo XIV° si sapeva che si poteva
ottenere la "latitudine" misurando l'altezza
della Polare al di sopra dell'orizzonte con
uno degli strumenti citati, ed apportando una
piccola correzione che veniva stabilita in
base alla posizione delle altre stelle dell'Orsa
Minore.
Fu però soltanto nel secolo seguente,e
precisamente nel 1473,che Giovanni di
Koenigsberg,detto Regiomontanus, pubblicò
le prime Tavole di declinazione del Sole, che
permisero ai naviganti di determinare la
"latitudine con l'osservazione dell'altezza
meridiana "
Da " Le Vie d'Italia " del 7 Luglio 1955-COME SI NAVIGA SUL MARE
Astrolabio (sinistra). A destra, confronto tra l'uso della Balestriglia e del Quadrante di Davis. Il secondo
strumento consentiva di osservare il sole voltandogli le spalle, in maniera da ridurre l'effetto dei raggi diretti
sulla vista dell'operatore.
Il problema della longitudine
• Il primo sovrano a mettere in palio un premio fu il re di
Spagna Filippo II, nel 1567. Allo "scopritore della
longitudine" venivano offerti un dono di 6000 ducati e una
rendita vitalizia di 2000 ducati, nonché 1000 ducati per
coprire le eventuali spese.
• Uno dei concorrenti all'aggiudicazione del premio fu Galileo
Galilei, che nel 1616 scrisse alla corte spagnola proponendo
un sistema di misurazione del tempo assoluto tramite i
satelliti di Giove.
• Galileo osservò per la prima volte le lune gioviane nel 1610:
e verso la fine del 1612 era riuscito a compilare le tavole dei
loro movimenti, con le quali si riusciva a prevedere la loro
posizione con un anticipo di parecchi mesi.
• Una corrispondenza durata più di sedici anni non riuscì a
persuadere gli esperti spagnoli delle virtù di questo metodo.
“..il giorno 7 gennaio del corrente anno 1611, all’una
di notte , mentre osservavo gli astri celesti con il
cannocchiale, mi si presentò Giove, e dato che mi
ero allestito uno strumento davvero eccellente, mi
avvidi che gli stavano vicino tre Stelline invero
piccole , ma assai luminose…e mi destarono una
certa meraviglia perché, per il fatto che sembravano
disposte secondo una precisa linea retta e parallela
all’Eclittica e più luminosa di altre di pari
grandezza.”
Con queste parole Galileo Galilei descrisse la
scoperta dei satelliti di Giove nel Sidereus Nuncius.
L’idea di Galilei era di sfruttare Giove come orologio
visibile da ogni punto della Terra, per questo
servivano effemeridi accurate per il calcolo dei diversi
fenomeni ed un telescopio che potesse essere
utilizzato su una nave.
Galilei disegnò anche un copricapo con incorporato
un cannocchiale, il celatone, che poteva essere
utilizzato in navigazione per osservare i satelliti
medicei.
Lo sperimentò sulla terraferma a Livorno e spedì un
suo studente a sperimentarlo su una nave, ma come
ammise lui stesso, lo strumento non era molto
affidabile, “bastava un battito del cuore” per far uscire
Giove dal campo visivo.
Il cannocchiale di Galileo
L’oculare negativo intercetta i raggi convergenti provenienti
dall’obiettivo rendendoli paralleli e formando così, all’infinito
(posizione afocale), un’immagine virtuale, ingrandita e diritta.
Il campo di vista (CdV) del
cannocchiale di Galileo e`
determinato in larga misura
dalla pupilla dell‘ osservatore
e le dimensioni di questa
dipendono dall'illuminamento
dell'oggetto.
Sebbene il CdV sia piccolo,
l'osservatore puo` muovere
la testa a destra e sinistra,
alto e basso e vedere una
regione maggiore
dell'oggetto. E` cio` che si
chiama un CdV virtuale.
Il campo di vista che può essere osservato è determinato
dall’intervallo dei coni provenienti dall’obiettivo che
completamente, o parzialmente, entrano nella pupilla
dell’osservatore.
Nello schema riportato il raggio verde provieniente dal centro
della Luna entra completamente nella pupilla (nera) dell’occhio.
Ma I raggi blu e rosso, provenienti dal lembo superiore ed
inferiore mancano completamente la pupilla dell’osservatore.
Ne consegue che solo la regione intorno al centro della Luna è
visibile.
Galileo, nel 1612,
cerca di raffinare le
osservazioni al
telescopio per
costruire una teoria
dei moti dei satelliti
gioviani.
Realizza un
micrometro costituito
da un braccio
graduato orientabile
in senso radiale e
scorrevole lungo
l’asse dello
strumento.
• Con l’occhio sinistro Galileo traguardava il
braccio sporgente dal tubo del telescopio,
mentre con il destro il campo nell’oculare; la
visione combinata restituiva un’immagine in cui il
braccio graduato si sovrapponeva a Giove e ai
suoi satelliti, permettendo cosi di fare le misure
necessarie.
Io, superposed in front of the giant planet it circles. To the left of Io is a dark spot that is
its own shadow. Credit: Cassini Imaging Team, Cassini Project, NASA
• Per tutto il 1611 osservò le lune di Giove, ne
calcolò le orbite e contò le volte che esse
sparivano dietro l’ombra del pianeta; poiché
queste eclissi avvenivano con grande
frequenza, mille volte l’anno, ipotizzò che la
loro regolarità poteva funzionare da orologio
celeste per le misure di longitudine.
• Bisognava solo avere a disposizione delle
tabelle con le previsioni precise dei
fenomeni.
Istoria e Dimostrazioni intorno alle macchie solari
Galileo dimostra per mezzo
della geometria che le macchie
sono vicinissime, e forse
contigue, alla superficie del
Sole.
La prova più stringente che Galileo ha della
correttezza del moto copernicano annuo
della Terra fu il suo successo nel prevedere
le eclissi dei satelliti di Giove. Prova che
viene solo menzionata in un’appendice alle
sue lettere sulle macchie solari.
Io, Europa, Ganimede e
Callisto, sono osservabili
dalla Terra anche con
piccoli cannocchiali; nel
loro moto di rivoluzione
intorno al pianeta esse
consentono l’osservazione
di interessanti fenomeni,
come Eclissi, Occultazioni
e Transiti del satellite
stesso o della sua ombra
davanti al pianeta.
Interludio 2: la luce rallenta e la Francia si restringe
•Alla morte di Galileo, nel 1642, le tavole non avevano ancora
la precisione sufficiente per consentire la determinazione della
longitudine con una sufficiente precisione.
•Le prime tavole ragionevolmente accurate furono quelle
dell’astronomo Gian Domenico Cassini nel 1668. Fu Cassini a
fondare l’osservatorio di Parigi, e fu per mezzo delle sue tavole
che Olaeus Rømer, astronomo danese, fu capace, nel 1676, di
trovare un errore sistematico di circa 10 minuti nei tempi di
eclisse dei satelliti gioviani, il cui periodo coincideva con il
periodo sinodico (da opposizione ad opposizione) di Giove.
•Rømer correttamente interpreta questo risultato per
dimostrare che la luce non viaggia istantaneamente.
Interludio 2: la luce rallenta e la Francia si restringe
•Negli anni 70 del 1600 gli astronomi francesi, sotto la
direzione di Cassini, iniziarono ad osservare le posizioni
dei satelliti di Giove in diverse località della Francia.
•La mappa risultante della Francia, finita nel 1679, dimostrò
che la costa occidentale disegnata nelle mappe esistenti era di
un grado troppo ad Ovest rispetto alla realà.
•Anche le coste del Mediterraneo andavano ridisegnate.
•Si racconta che re Luigi XIV disse, dopo aver visto la nuova
mappa, che aveva perso più territorio per colpa dei suoi
astronomi che per colpa dei suoi nemici.
Epilogo
• Il 16 giugno 1714 il parlamento inglese emanò il cosiddetto
Longitude Act, con il quale si stabilì "una ricompensa per la
persona o le persone che scopriranno la longitudine".
• L'ammontare del premio fu differenziato a seconda della
precisione raggiunta: 10.000 sterline se la longitudine fosse
stata determinata con un errore di un grado, 15.000 se
l'errore fosse stato di due terzi di grado, e 20.000 se l'errore
fosse stato inferiore al mezzo grado.
• Per comprendere il valore di questo premio, basti ricordare
soltanto che lo stipendio annuale di Flamsteed era di 100
sterline (tasse escluse...).
• Il Longitude Act istituì anche un collegio di giudici di
grandissimo prestigio, tutti insigniti dell'ordine della
Giarrettiera, che divenne noto come Board of Longitude
(Commissione della Longitudine).
Epilogo
• Nel 1715 John Harrison, un carpentiere autodidatta di Foulby,
nello Yorkshire, costruì il suo primo orologio. Una dozzina di
anni dopo realizzò uno strumento con un pendolo "a graticola",
formato da nove piccole barre in acciaio e in ottone alternate,
capaci di neutralizzare gli sbalzi di temperatura.
• Nel 1730 Harrison andò a Londra portando con sé il suo nuovo
pendolo: dopo aver appreso quanto era richiesto per vincere il
premio della longitudine, egli si incontrò con Halley, divenuto
Astronomo Reale dopo la morte di Flamsteed, il quale lo
consigliò di non chiedere finanziamenti alla Commissione della
Longitudine, ma piuttosto di cercare soldi da altre fonti.
• In effetti Halley sapeva che i membri della Commissione, in
gran parte scienziati e astronomi, erano favorevoli al metodo
delle distanze lunari e perciò erano prevenuti nei confronti di
altri sistemi.
Epilogo
• Nel 1759 Harrison presentò il suo
strumento definitivo, l'H4, che venne
imbarcato sul Deptford, in traversata
atlantica da Londra alla Giamaica. Il
viaggio durò ottantuno giorni: il ritardo
accumulato fu di soli cinque secondi.
• Le condizioni stabilite dal Longitude Act
erano soddisfatte: tuttavia la
Commissione della Longitudine accampò
una serie di pretesti pur di non dichiarare
Harrison vincitore.
• Soltanto dopo una petizione a re Giorgio
III, nel 1772 un John Harrison ormai
quasi ottantenne si vide assegnare la
metà del premio prestabilito, vale a dire
10.000 sterline.
Cronometri di Harrison; da sinistra a
destra H1, H2, H3, e H4.
© National Maritime Museum, London.
Bibliografia
• Longitude, Dava Sobel, Fourth Estate
• Esercitazioni di Astronomia, A. Righini
• Misure di longitudine con le “lune” di giove,
Lucia Corbo,
• The Galileo Project
http://galileo.rice.edu/sci/observations/longitude.
html
• Galileo scopre nuovi mondi, I. Dal Prete,
Coelum, 2010, 135, 28-38
• Notiziario 11 & 12 della AAT, M. Murara,1998