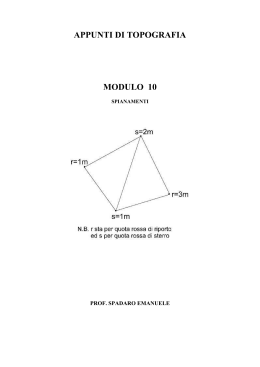
ISTITUTO TECNICO PER GEOMETRI
CORSO DI TOPOGRAFIA
Programma modulare ON LINE per la classe V I.T.G.
MODULO 1: AGRIMENSURA
U.D. 1: misure delle aree con metodi numerici: formula di Gauss.
U.D. 2: divisione dei terreni a valenza costante.
U.D. 3: rettifica e spostamenti di confini tra terreni a valenza costante.
MODULO 2: SPIANAMENTI
U.D. 1: calcolo dei volumi di solidi prismatici; spianamenti con piani orizzontali ed inclinati su
piani quotati e a curve di livello.
MODULO 3: STRADE
U.D. 1: elementi costruttivi e normativi di un’opera stradale.
U.D. 2: elementi del progetto di un’opera stradale.
U.D. 3: movimenti di terra.
Contenuti dell’Unità Didattica.
Misure delle aree con metodi grafici e numerici.
ESPLICITAZIONE DEI CONTENUTI DELL’U.D. 1
L’agrimensura è quella disciplina che si occupa della misura delle aree delle superfici dei terreni
della loro divisione, della rettifica e spostamento di confine.
La misura che viene prese in considerazione e quella relativa alla superficie agraria, cioè quella
relativa alla proiezione su di un piano orizzontale della superficie fisica o naturale del terreno.
L’unità di misura delle aree è il m2, mentre ai fini agrari e nei documenti catastali vengono utilizzati
le seguenti unità di misura:
- centiara (ca) = 1 m2
- ara (a) = 100 m2
- ettaro (Ha) = 10.000 m2
Una porzione più o meno grande di terreno viene definita appezzamento e può essere delimitata in
tutto od in parte da linee poligonali o curvilinee, naturali, quali fossi, corsi d’acqua, strade, o linee
artificiali costruite dall’uomo.
Il calcolo dell’area di una superficie agraria di un appezzamento può essere effettuato con metodi
diversi e che vengono riportate di seguito.
- Metodi numerici.
L’area viene determinata tramite le misure lineari e angolari rilevate direttamente sul terreno.
La precisione del risultato dipende esclusivamente dalla precisione delle misure effettuate.
- Metodi grafici.
In questo caso si deve disporre della rappresentazione grafica dell’appezzamento di terreno in
scala opportuna; la sua superficie poligonale, mediante costruzioni geometriche, viene
trasformata in una figura elementare equivalente (generalmente un triangolo) nella quale si
misurano gli elementi necessari per poterne calcolarne la superficie con formule applicabili a
figure geometriche elementari (tre o quattro lati).
Le costruzioni geometriche consentono di ridurre al minimo il numero delle misure da ricavare
direttamente sul grafico, però il metodo non permette una grande precisione a causa degli errori
di graficismo e di stima delle misure.
- Metodi grafici-numerici.
Per applicare questi metodi bisogna disporre della rappresentazione grafica dell’appezzamento di
terreno in data scala; in questo caso vengono misurati i dati necessari con opportune formule.
In questo caso la precisione è influenzata da errori di graficismo e dalla stima delle misure.
- Metodi meccanici.
L’area della superficie viene determinata adoperando strumenti particolari (Planimetri) con i
quali si opera direttamente sulla rappresentazione grafica del terreno.
Il metodo si presenta molto rapido, ma poco preciso, in quanto agli errori di graficismo e di stima
si aggiungono anche quelli strumentali.
2 - Metodi numerici
Metodi numerici sono procedimenti di calcolo che utilizzano formule già note dalla geometria e
dalla trigonometria e che vengono sviluppate con i dati numerici (lati, angoli, coordinate ecc.)
misurati nel rilievo del contorno dell’ appezzamento.
Questi metodi sono talvolta più laboriosi fra tutti quelli di calcolo delle aree, tuttavia sono anche i
più precisi in quanto risentono esclusivamente degli eventuali errori commessi nelle misurazioni
effettuate sul terreno durante il rilievo.
La scelta della procedura geometrica da impiegare per calcolare l’area della superficie agraria di un
appezzamento dipende essenzialmente dal tipo di rilievo effettuato in campagna per definire il
contorno dell’appezzamento.
2.1 - Area di un appezzamento rilevato per allineamenti o per trilaterazione
Se un appezzamento è stato rilevato per allineamenti e squadri, l’area totale viene calcolata come
somma delle aree del figure elementari generalmente triangoli e trapezi, in cui gli allineamenti
principali e gli squadri dividono l’appezzamento.
Nel calcolo vengono impiegate le misure lineari effettuate lungo gli allineamenti in fase di rilievo.
Nel caso, ad esempio, della figura 1, l’appezzamento di forma poligonale ABCDEFG è stato
rilevato mediante l’allineamento principale e diretto secondo la diagonale maggiore,e gli squadri
BB’. CC DD’, FF’e GG’ ottenuti tracciando dai vertici le rispettive perpendicolari all’allineamento
AE.
Figura 1 – area di un
appezzamento rilevato per
allineamenti e squadri. Essa
viene ottenuta dalla somma
delle
aree
delle
figure
elementari 1, 2, 3,…,7.
L’area totale si ottiene sommando quelle delle singole figure i cui elementi sono stati misurati in
campagna durante il rilievo.
Se un appezzamento è stato rilevato per trilaterazione l’area totale si calcola sommando le aree dei
singoli triangoli in cui è stato suddiviso l’appezzamento fase di rilievo. Si applica poi la formula di
Erone impiegando in ogni triangolo lunghezze dei suoi tre lati misurati direttamente.
Nel caso, ad esempio, della figura 2, l‘appezzamento poligonale ABCDEF stato rilevato per
trilaterazione suddividendolo nella maglia di triangoli PAB, PBC, PCD, PDE, PEF e PAF, di
ciascuno dei quali vengono misurati i tre lati. L’area di ogni triangolo viene calcolata con la formula
di Erone. La somma delle aree delle superfici triangolari esprime l’area dell’appezzamento
ABCDEF.
Figura 2
L’area di un appezzamento
rilevato per trilaterazione. Esso
viene scomposto in triangoli
dei quali vengono misurati i
lati. Sommando le aree di
ciascun triangolo usando la
formula di Erone si ottiene
l’area complessiva.
2.2 - AREA DI UN APPEZZAMENTO RILEVATO PER CORDINATE CARTESIANE
Se il contorno di un appezzamento è stato rilevato per coordinate cartesiane, se ne può calcolare
l’area mediante le ascisse e le ordinate dei vertici i cui valori sono stati misurati in campagna o sono
stati calcolati a tavolino.
Consideriamo l’appezzamento a forma quadrilatera di figura 3. Abbassando da ogni vertice del
contorno le perpendicolari all’asse delle ascisse, vengono definiti i trapezi ABBOAO, BCCOBO ,
CDDOCO, e DAAODO; con S1, S2, S3, S4 le rispettive aree, si vede subito che l’area S
dell’appezzamento ABCD è data da:
S = S1+ S2+ S3+ S4
Esprimendo le aree dei trapezi in funzione delle coordinate note dei rispettivi vertici, si ottiene:
S = 1/2 (YA+ YB) (XB - XA) + 1/2(YB + YC) (XC - XB) +
+ 1/2 (YC + YD) (XD - XC) — 1/2 (YD + YA) (XD – XA)
Quindi, cambiando disegno all’ultimo termine della sommatoria (invertendo l’ordine dell’ultimo
binomio) e raccogliendo il termine comune 1/2, si ha:
S = l/2 [(YA+ YB) (XB - XA) (YB + YC) (XC - XB) +
(YC + YD) (XD - XC) + (YD + YA) (XA – XD)]
(1)
La (1) consente di calcolare l’area di un appezzamento in funzione delle coordinate cartesiane dei
vertici. Analizzando la formula, si può notare che il numero dei termini della sommatoria coincide
con quello dei vertici dell’appezzamento. Inoltre, percorrendo il poligono in senso orario e
considerando un vertice alla volta, ciascun termine è costituito dal
Figura 3
Area di un appezzamento cui
contorno è stato rilevato per
coordinate cartesiane. La
procedura richiede che i
vertici siano numerati in senso
orario.
prodotto della somma delle
ordinate del vertice considerato e di quello successivo per la differenza tra le ascisse del vertice
successivo e di quello considerato.
Pertanto l’espressione (1) può essere estesa e applicata al calcolo dell’area di un appezzamento
costituito da un generico numero n di vertici.Indicando con i l’ordine del vertice generico si ha:
(2)
Sia la (1) che, di conseguenza, la (2) possono essere scritte in forma più semplice. Infatti, eseguendo
i prodotti nel secondo membro della (1) e semplificando si ottiene:
raccogliendo
le y,si può scrivere:
(3)
Generalizzando la (3), ricavata con un appezzamento di forma quadrilatera ed estendendola a un
poligono costituito da n vertici, si ottiene:
(4)
Se nella figura 3 si tracciano le perpendicolari dai vertici all’asse delle ordinate, anziché all’asse
delle ascisse in luogo rispettivamente della (2) e della (4) si ottengono facilmente le seguenti:
(5)
(6)
La (4) e la (6) sono dette anche formule di Gauss e possono essere enunciate nel la seguente forma:
L’area d un appezzamento a contorno poligonale è data dalla semisomma dei pro- dotti delle
ordinata (o dell’ascissa) d ciascun vertice per a differenza tra ascissa (o l’ordinata) del vertice
seguente (o precedente) e l’ascissa (o l’ordinata) del vertice precedente (o seguente).
Nel caso in cui il perimetro dell’appezzamento venga percorso in senso anti-orario, l’applicazione
delle (2), (4), (5) e (6) dà un’area negativa, ma questo nulla toglie alla validità delle precedenti
formule in quanto le aree vengono considerate sempre positive assumendone il valore assoluto.
Al fine di evitare errori banali ma frequenti, va ricordato che i valori numerici delle coordinate
vanno sempre considerati con i loro segni algebrici.
3 – METODI GRAFICI
I metodi grafici consistono nel trasformare, con opportuno procedimenti grafici, un appezzamento
di forma poligonale disegnato in scala in un triangolo o in un rettangolo equivalenti e nel calcolarne
l’area mediante a base e l‘altezza misura sul grafico.
Questi metodi sono rapidi, talvolta eleganti, ma poco attendibili per le inevitabili approssimazioni
che si commettono sia nella trasformazione grafica sia nella misura delle grandezze direttamente sul
disegno, anche se il numero di queste ultime viene ridotto al minimo.
3.1 Trasformazione di un poligono in un triangolo equivalente
Metodo del vertice fisso
Consiste nel trasformare un appezzamento ad esempio quello pentagonale ABCDE di figura 1 in
modo che un suo vertice, ad esempio A sia uno di quelli che definiscono il triangolo equivalente al
poligono.
Si traccia dal vertice B la parallela alla diagonale AC fino a incontrare in B’il prolungamento del
lato CD. Congiungendo A con B’viene definito il quadrilatero AB’DE che è equivalente al poligono
dato ABCDE. Infatti al pentagono è stato tolto il triangolo ABC ed è stato aggiunto il triangolo
AB’C. I due triangoli sono equivalenti per avere la stessa base AC e la medesima altezza,
rappresentata dalla distanza tra le due rette AC e BB’ parallele per costruzione. Pertanto il
pentagono dato è stato trasformato in un quadrilatero equivalente.
Analogamente si trasforma il quadrilatero AB’DE nel triangolo equivalente AB’’E. Si traccia dal
vertice B’la parallela alla diagonale AD fino a incontrare in B’’ il prolungamento del lato ED.
Congiungendo A con B”, viene definito il triangolo AB”E che è equivalente al quadrilatero AB’DE.
Infatti al quadrilatero è stato
Figura 1
Trasformazione
di
un
poligono in un triangolo
equivalente con un vertice
fisso.
L’area
viene
calcolata misurando b e h
sul disegno.
tolto il triangolo AB’D ed è
stato aggiunto il triangolo
AB”D. I due sono equivalenti per avere la stessa base AD e la medesima altezza, rappresentata dalla
distanza tra le due rette AD e B’B”,parallele per costruzione.
Per calcolare l’area dell’appezzamento pentagonale ABCDE, basta determinare quella del triangolo
equivalente AB”E misurandone graficamente un qualunque e la relativa altezza. Conoscendo la
scala del disegno si possono avere le misure reali espresse in metri così da calcolare l’area in m2.
Metodo del lato fisso
Consiste nel trasformare un appezzamento per esempio quello esagonale ABCDEF di figura 2 in
modo che un lato dell’appezzamento ad esempio DE si trovi uno dei lati del triangolo equivalente al
poligono. Per comprendere la costruzione occorre tenere presente quanto è stato detto nel problema
precedente.
Si traccia dal vertice C la parallela alla diagonale ED fino a incontrare in B’ il prolungamento del
lato DE. Si congiunge B con D’in modo da sostituire il triangolo BCD con quello equivalente
EDD’. L’esagono ABCDEF è stato così trasformato nel pentagono equivalente ABD’EF. Quindi si
traccia da B la parallela AD’ fino a incontrare in D” il prolungamento del lato DE. Si congiungono i
A e D” sostituendo così al triangolo ABD’ quello equivalente AD’D”. Il pentago ABD’EF è stato
così trasformato nel quadrilatero equivalente AD”EF. Infine si traccia dal vertice F la parallela alla
diagonale AE fino a incontrare nel punto E’ il prolungamento del lato DE. Congiungendo i punti A
ed E’ si sostituisce al triangolo AEF quello equivalente AEE’, in modo che il quadrilatero AD”EF e
il triangolo AD”E’ risultano equivalenti.
Per calcolare l’area dell’appezzamento esagonale A BCDEF basta determinare
quella del triangolo equivalente AD”E’, come visto in precedenza.
3.2 - Trasformazione di un trapezio in un rettangolo equivalente di base data
Consideriamo il trapezio ABCD di figura 2 che deve essere trasformato nel rettangolo equivalente
di base assegnata OE = b.
Si traccia la base media MN del trapezio e si proietta il punto M in M’sulla verticale condotta
dall’estremo E della base. Si traccia dal vertice A la parallela a
Figura 2
Trasformazione
di
un
poligono in un triangolo
equivalente con un lato
fisso. L’area viene calcolata
misurando graficamente un
lato e la relativa altezza.
OM’ fino a incontrare in H la base BC del trapezio. Il segmento BH = h è l’altezza cercata in quanto
il rettangolo di base b e altezza h è equivalente al trapezio ABCD. Infatti dalla similitudine dei
triangoli ABH e OEM’ possiamo scrivere:
b : EM’ = AB : h
b x h = EM’ x AB
Il segmento EM’ è uguale a MN e quindi rappresenta la media delle basi del trapezio. Pertanto il
secondo membro della (1) è l’espressione dell’area del trapezio ÀBCD. Poiché il primo membro
rappresenta l’area del rettangolo di base b e altezza h, risulta dimostrata l‘equivalenza del trapezio
e del rettangolo.
La costruzione resta sostanzialmente immutata se si riduce a un rettangolo equivalente un rettangolo
anziché un trapezio. In questo caso basta che una delle basi, AD o BC della figura 4, sia nulla. Nella
figura 5 abbiamo trasformato il triangolo rettangolo ABC nel rettangolo equivalente di base
assegnata b.
Figura 4
Trasformazione di un trapezio in un rettangolo equivalente di base b. Questa viene scelta
arbitrariamente dall‘operatore.
Figura 5
Trasformazione di un triangolo in un rettangolo equivalente di base b.
4 – METODI MECCANICI
Definizione di metodi meccanìci consentono di misurare l’area di un appezzamento operando con
strumenti, detti planimetri e secondo particolari criteri sulla sua rappresentazione grafica
appositamente redatta in scala (mappa).
Questi ultimi metodi sono i più rapidi ma spesso poco precisi. Infatti, oltre a essere influenzati dagli
errori elencati per tutti gli altri metodi, risentono anche di eventuali imperfezioni strumentali. In
questo ambito vengono trattati soltanto i planimetri, che sono gli strumenti più in uso nel calcolo
meccanico. Per gli altri mezzi meccanici si rimanda il lettore a trattati di maggior ampiezza e alle
istruzioni che sempre accompagnano lo strumento.
4.1 - Planimetro potare di Amsler
Questo strumento è schematicamente rappresentato in figura 1.
Figura 1
Planimetro polare di Amsler
L’asta tracciante porta all’estremità il puntatore costituito da una lente d’ingrandimento con
incastonato un dischetto che permette di esplorare il percorso del perimetro dell’appezzamento da
esplorare. Tale asta è collegata ad un’altra asta, chiamata braccio polare, che ha una estremità fissa
e, detto polo, al quale essa ha la possibilità di ruotare. Il polo viene alloggiato un foro praticato su
un disco pesante, recante generalmente tre puntine nella patte inferiore. In questo modo il polo non
subisce spostamenti in fase operativa Al l’estremo sinistra dell’asta tracciante è applicata una rotella
scorrevolissima e portante un tamburo diviso in cento parti di graduazione. Al bordo del tamburo è
applicato un nonio che permette di apprezzare il decimo della parte di rotella: ne consegue che
l’unità di graduazione si spinge al millesimo di giro della rotella. Lo strumento è dotato di un
dispositivo per riportare a zero la lettura iniziale e di un disco contagiri nel quale si possono leggere
fino a 10 giri completi della rotella.
4.2 – ALTRI TIPI DI PLANIMETRI
Il planimetro lineare a rulli (fig. 2) è caratterizzato da un carrello costituito rulli di ottone cromato
calettati su uno stesso albero. Il carrello a rulli è collegato al carrello contatore mediante un giogo,
che sostituisce il braccio polare,munito di perno sferico. La superficie cilindrica dei rulli è zigrinata
in modo da impedire sbandamenti e assicurare un moto rettilineo. Esso è particolarmente indicato
per la misura delle aree di figure allungate o di diagrammi a nastro di strumenti registratori.
I planimetri elettronici digitali (figg. 2 e 3) possono essere polari o lineari a rulli. Si imposta
preventivamente l’unità di misura e la scala cartografica, la misura dell’area compare su un display
a cristalli liquidi. La lunghezza dell’asta segnatrice può essere modificata ruotando una apposita
vite. Questi strumenti consentono una buona precisione, circa 0,1%.
I planimetri elettronici digitali di ultima generazione (fig. 4) sono anche perimetratori, cioè
forniscono oltre all’area anche la lunghezza del contorno tracciato ed eventuali distanze tra punti.
Essi sono corredati di utili funzioni che li rendono pratici, semplici da usare ed efficaci. Con questi
planimetri il calcolo della superficie di figure a contorno poligonale può essere effettuato
posizionando il puntatore sui vertici della figura, senza la necessità di tracciare tutto il conto. In
questo modo l’operazione di misura diviene assai più rapida e si ottiene un significativo
miglioramento della precisione di misura.
Figura 2 – Planimetro lineare a rulli
Figura 3 – Planimetro polare digitale
Figura 4 – planimetro
digitale a rulli
Figura 4 – planimetro digitale perimetratore
Frazionamenti
Una delle problematiche che si presenta frequentemente nell’attività di un geometra,è l’esecuzione
di un frazionamento di una superficie agraria in più parti direttamente o inversamente proporzionali
a determinati coefficienti.
Occorre al riguardo fare una distinzione fra terreni c.d. a valore unitario costante, e terreni a valore
unitario diverso.
I primi sono quei terreni il cui unico parametro di riferimento è la superficie avendo ogni metro
quadro lo stesso identico valore dell’altro.
Nei secondi invece entra in gioco anche il valore delle singole unità del terreno per cui non è
sufficiente suddividere l’area per effettuare un frazionamento,ma bisogna tenere conto anche di altri
parametri.
Per semplicità di trattazione ci limiteremo ad affrontare lo studio della prima tipologia di terreni.
Primo caso:
Frazionamento di un terreno a valore unitario costante in tre parti direttamente proporzionali ai
coefficienti m1, m2, m3.
Si procede ad impostare una proporzione tra il tutto da frazionare e le singole parti, incognite,
risultato del frazionamento stesso, sulla base dei coefficienti di proporzionalità indicati.
S:S1= (m1+m2+m3):m1;
S:S2= (m1+m2+m3):m2;
S:S3=(m1+m2+m3):m3.
Impostate le tre proporzioni risulta immediato ricavare le tre incognite S1 ,S2 ,S3 , cercate.
S1=
S x m1
――――――――;
(m1+m2+m3)
S2=
S x m2
――――――――;
(m1+m2+m3)
S3=
S x m3
―――――――― .
(m1+m2+m3)
Secondo caso:
Frazionamento di un terreno a valore unitario costante in tre parti inversamente proporzionali ai
coefficienti m1, m2, m3.
Si procede ad impostare le stesse proporzioni del caso precedente nel seguente modo:
S:S1= (1⁄m1+1⁄m2+1⁄m3): 1⁄m1;
S:S2= (1⁄m1+1⁄m2+1⁄m3): 1⁄m2;
S:S3=(1⁄m1+1⁄m2+1⁄m3): 1⁄m3
Le incognite si ricavano con la modalità già nota.
S1=
S x 1⁄m1
――――――――;
(1⁄m1+1⁄m2+1⁄m3)
S2=
S x 1⁄m2
――――――――;
(1⁄m1+1⁄m2+1⁄m3)
S3=
S x 1⁄m3
―――――――― .
(1⁄m1+1⁄m2+1⁄m3)
Terzo caso:
Frazionamento di un terreno a valore unitario costante in tre parti direttamente proporzionali ai
coefficienti m1, m2, m3, e inversamente proporzionali ai coefficienti n1, n2, n3.
Si procede nello stesso modo con le seguenti varianti:
S:S1= (m1⁄ n1+ m2⁄ n2+ m3⁄ n3): m1⁄ n1;
S:S2= (m1⁄ n1+ m2⁄ n2+ m3⁄ n3): m2⁄ n2;
S:S3=( m1⁄ n1+ m2⁄ n2+ m3⁄ n3): m3⁄ n3
Le incognite, di conseguenza, saranno:
S1=
S x(m1⁄ n1)
――――――――;
(m1⁄ n1+ m2⁄ n2+ m3⁄ n3)
S2=
S x (m2⁄ n2)
――――――――;
(m1⁄ n1+ m2⁄ n2+ m3⁄ n3)
S3=
S x (m3⁄ n3)
―――――――― .
.
(m1⁄ n1+ m2⁄ n2+ m3⁄ n3)
Libro di testo utilizzato.
Titolo: misure rilievo progetto - Vol. III
Autori: Renato Cannarozzo, Lanfranco Cucchiarini, William Meschieri
Casa editrice: Zanichelli
Contenuti dell’Unità Didattica 1.
Calcolo dei volumi di solidi prismatici; spianamenti con piani orizzontali ed inclinati su piani
quotati e a curve di livello.
PREMESSA
Lo spianamento è un insieme di operazioni e calcolo dirette a modificare la superficie fisica
irregolare del terreno, trasformandola in una superficie piana, orizzontale o inclinata, mediante
movimenti di terra.
Gli spianamenti, consentono la sistemazione superficiale del terreno, hanno notevole
importanza in diversi settori, non solo in quello delle costruzioni civili, industriali e di edilizia
pubblica per la formazione di un piano di posa delle fondazioni, e quello delle costruzioni di strade
ed aeroporti, ma anche in quello agricolo ed ambientale per la sistemazione di terreni al fine di un
maggior e più razionale impiego delle macchine e per la formazione di parchi, giardini pubblici e
spazi attrezzati.
Il progetto di uno spianamento è effettuato, generalmente, su una rappresentazione del terreno
a piano quotato; Solo quando la zona interessata è molto estesa e piuttosto accidentata si utilizza
una rappresentazione a curve di livello che, pur richiedendo operazioni di rilievo più lunghe e
complesse, permette una descrizione del terreno più aderente alla realtà.
Il piano di spianamento (detto piano di progetto) è il piano che dovrà presentare il terreno
dopo aver effettuato le necessarie operazioni di movimento terra per modificare la superficie
naturale del terreno.
Viene definita quota di progetto di un punto generico del terreno la quota che tale punto viene
ad avere sul piano dello spianamento; la differenza tra la quota di progetto Q’ di un punto e la sua
quota sul terreno Q (quota ortometrica del terreno) è detta quota rossa q, ovvero q = Q’ – Q.
In corrispondenza della verticale passante per un punto generico della superficie naturale del
terreno, può risultare che:
- il piano di progetto passa al di sopra per un punto del terreno; in questo caso la quota rossa del
punto è positiva e rappresenta una ordinata di riporto in quando in corrispondenza del punto deve
essere riportato terreno;
- il piano di progetto passa al di sotto per un punto del terreno; in questo caso la quota rossa del
punto è negativa e rappresenta una ordinata di scavo in quando in corrispondenza del punto si
deve scavare terreno;
- il piano di progetto in un punto coincide con quella del terreno; in questo caso la quota rossa del
punto è zero ed il punto viene detto di passaggio.
Un progetto di uno spianamento è affrontato secondo lo schema di seguito riportato.
a) Rilievo plano-altimetrico della superficie naturale della zona di terreno interessata dallo
spianamento.
b) Restituzione grafica del rilievo secondo un piano quotato (o piano a curve di livello);
c) Calcolo delle aree delle varie falde triangolari piane che formano la superficie naturale;
d) Definizione della tipologia del piano di spianamento;
e) Calcolo delle quote di progetto Q’ di tutti i punti caratteristici del terreno;
f) Calcolo delle quote rosse dei punti caratteristici;
g) Determinazione della posizione dei punti di passaggio e delle linee di passaggio che definiscono
le zone di sterro e di riporto;
h) Calcolo dei volumi di sterro e di riporto.
INTRODUZIONE
Gli spianamenti trovano applicazione pratica in tutti quei casi in cui occorre si sistemare la
superficie di un terreno di modesta estensione per costruirvi impianti sportivi, fabbricati civili e
industriali, strade, aeroporti, ecc. Possono essere progettati su terreni rappresentati sia con piani
quotati che con curve di livello. E più frequente il primo caso perché la rappresentazione con curve
di livello comporta un rilievo molto oneroso e quindi consigliabile solo per zone fortemente
accidentate dove occorre descrivere in modo più fedele l’andamento del terreno.
Il piano secondo cui deve essere sistemata la superficie fisica del terreno è definito piano di
progetto. La quota del piano di progetto in corrispondenza della verticale condotta da un punto
qualsiasi del terreno è definita quota di progetto del punto.
La differenza tra la quota di progetto di un punto e la corrispondente quota del terreno è la d quota
rossa del punto.
Se la quota rossa è positiva (ordinata di riporto) il piano di progetto passa, in quel punto, ai di sopra
del terreno, mentre se la quota rossa è negativa (ordinata di sterro) il piano passa al disotto del
terreno, Per realizzare uno spianamento occorre effettuare lavori di scavo e lavori di riporto. Gli
scavi vengono effettuati nelle zone che si trovano al di sopra del piano di progetto (insieme dei
punti con quota rossa negativa), i riporti in quelle che si trovano al disotto del piano di progetto
(insieme dei punti con quota rossa positiva).! punti del terreno che hanno la quota coincidente con
quella di progetto, cioè i punti che appartengono contemporaneamente al piano di progetto e alla
superficie fisica, sono detti punti di passaggio e hanno quota rossa nulla.
La spezzata che congiunge i punti di passaggio è definita linea di passaggio e separa la zona di
scavo da quella di riporto Il volume di terra compreso tra il piano di progetto e la zona di scavo è
detto volume di sterro, quello compreso tra piano di progetto e la zona di riporto è detto volume del
riporto.
Con le notazioni di figura 1, la superficie topografica da spianare è quella costituita dalle facce
triangolari ,ABP. BCP, CDP,DEP ed EAP,mentre π è il piano di progetto secondo il quale deve
essere effettuato lo spianamento. Le quote del piano di progetto nei punti A ‘, B’. C’, D’, E’, P’
rappresentano le quote di pro getto dei puntiA, B, C, D, E, P’. segmenti AA’, BB’, CC’, DD’ ed
EE’ rappresentano le quote rosse positive (ordinate di riporto) dei ponti A, B, C, D, E; il segmento
PP’ rappresenta la quota rossa negativa (ordinata di sterro) del punto P. I punti K, L, M. N, T
appartengono sia al piano π che al terreno e quindi sono punti di passaggio mentre la spezzata
KLMNT è la linea di passaggio. La zona di terreno interna alla spezzata è zona di scavo e il relativo
volume di sterro è costituito dai cnnei PP’KL, PP’LM, PP’MN, I-’P’Ni; PP’TK. La zona esterna
alla spezzata è di riporto e il relativo volume di riporto è costituito dai solidi ABLKB’A’,
BCMLC’B’, CDNMD’C, DENTD’E’, EATKE’A’.
In relazione al piano di progetto si possono avere i seguenti casi:
• piano di posizione prefissata (orizzontale o inclinato);
• piano di compenso fra sterro e riporto (orizzontale o inclinato).
Gli spianamenti orizzontali presentano l’inconveniente di non favorire o scolo delle acque e quindi
vengono realizzati quando queste non cadono direttamente
FIGURA 1 Le grandezze
caratteristiche dei progetti di
spianamento.
La
superficie
topografico deve essere sistemata
secondo il piano di progetto π. I
volumi di sterro e di riporto sono
composti da solidi prismatici.
sul terreno (caso di fabbricati costruiti sulla superficie spianata), oppure quando il terreno è
sufficientemente poroso ed esiste una fognatura con pendenza adeguata per lo smaltimento delle
acque raccolte. Gli spianamenti inclinati vengono effettuati, generalmente, per adattare i terreni a
determinate colture e per favorire lo scolo delle acque. Gli spianamenti più convenienti dal punto di
vista economico sono quelli in cui il volume di scavo eguaglia quello di riporto (spianamenti di
compenso). In questo modo non occorre portare terra a rifiuto (caso di spiano- menti con eccesso di
scavo), né prenderne da cave di prestito (caso di spianamenti con eccesso di riporto).
Rilevata la superficie fisica di un terreno con i metodi esposti nel secondo volume, restituita
graficamente la stessa mediante un piano quotato o a curve di livello o definito il piano di progetto,
uno spianamento viene realizzato attraverso le seguenti fasi:
1. Si determinano le quote di progetto Z’ in corrispondenza dei punti caratteristici del terreno.
Se il piano di progetto è orizzontale la quota di progetto è la stessa per tutti i punti del
terreno e coincide con la quota del piano.
2. Si calcolano le quote rosse h1 =Z’i - Zi dei punti caratteristici del terreno: se h1 < O
l’ordinata è di sterro, se > O l’ordinata è di riporto.
3. Si determina la posizione dei punti di passaggio, cioè dei punti di quota rossa nulla.
4. Si traccia la linea di passaggio congiungendo i successivi punti di passaggio in modo da
individuare le zone di sterro e le zone di riporto.
5. Si calcolano i volumi di sterro e i volumi di riporto.
Gli spianamenti vengono valutati soprattutto con il calcolo analitico. Le soluzioni grafiche,
imprecise e approssimate, sono superate dall’utilizzo dei computer che hanno reso più veloce e
accessibile il calcolo numerico.
1 - SPIANAMENTI SU PIANI QUOTATI CON PIANO DI PROGETTO DI
POSIZIONE PREFISSATA
1.1 – Spianamento di piano orizzontale di quota assegnata
Considerando la superficie topografica rappresentata dal piano quotato di figura 1 si deve
progettare lo spianamento secondo il piano orizzontale di progetto di qua H assegnata.
Le quote di progetto dei punti caratteristici sono uguali tra loro e coincidono tutte con la quota
H del piano di progetto:
Indicando con ZA , ZB , ZC , ZD , ZE , ZF, ZP le quote dei vertici delle falde triangolari, si
calcolano le quote rosse di tali punti. Supponiamo di avere ottenuto i seguenti risultati:
hA = H— ZA (valore positivo, ordinata di riporto)
hB = H— ZB (valore positivo, ordinata di riporto)
hC = H— ZC (valore positivo, ordinata di riporto)
hD = H— ZD (valore nullo, punto di passaggio)
hE = H— ZE (valore negativo, ordinata di sterro)
hF = H— ZF (valore nullo, punto di passaggio)
hP = H— ZP (valore negativo, ordinata di sterro)
Siamo allora in presenza di quote rosse sia positive che negative.
FIGURA 1 - Spianamento con piano orizzontale a quota H
assegnata. La linea di passaggio FLMND separa la zona di
riporto (in rosso) da quella di sterro (in giallo). Sul lato AP è
stata eseguita la costruzione grafica per determinare la
posizione di L.
I punti di passaggio sono disposti su due lati che congiungono due vertici del piano quotato con
quote rosse di segno opposto. Sono punti di passaggio anche i vertici la cui quota coincide con
quella del piano di progetto. Nel caso della figura 2 i punti F, L, M, N, D sono punti di passaggio.
Per minare la posizione di uno di essi, ad esempio L, facciamo riferimento figura 3 in cui è
rappresentato l’andamento del profilo del terreno secondo la congiungente AP. Essendo noti gli
elementi plano-altimetrici, sapendo che ZL = H e applicai proporzionalità tra gli elementi
corrispondenti di triangoli simili, si ha:
DAP : AP = DLP: LP
da cui:
Poiché DLP = hP è quota rossa di sterro e DAL= hA è quota rossa di riporto, osservando la figura 3
risulta evidente che DAP = hA + hp. Indicando con hs e hr, le quote rosse, rispettivamente, di sterro e
di riporto, con d Ia distanza AP e con dr, e ds, le distanze, rispettivamente, AL di riporto e LP di
sterro, la (1) può essere scritta nella forma più generale:
La distanza di riporto AL è data dall’analoga espressione:
Per determinare le posizioni dei punti di passaggio M e N si applicano le formule:
La determinazione della posizione dei punti di passaggio può essere eseguita con una semplice
costruzione grafica. Basta riportare alle estremità di un lato che congiunge due punti con quote
rosse di segno contrario, ad esempio AP, due segmenti con direzioni parallele e versi opposti che in
scala opportuna rappresentino le quote rosse hs ed hr , degli estremi del lato.
Le quote rosse hs e hr degli estremi del lato. La congiungente gli estremi di questi due segmenti
interseca il lato AP nel punto L di quota rossa nulla (flg. 2). Le direzioni dei due segmenti possono
essere scelte in modo arbitrario, per esempio perpendicolari al lato AP, basta che siano parallele fra
di loro.
La spezzata che congiunge i punti di passaggio è la linea di passaggio, cioè la traccia intersezione
tra il piano quotato e il piano di progetto e che divide la zona di sterro da quella di riporto.
Nel caso di figura 2 la linea di passaggio FLND divide la superficie topografica in due parti: quella
racchiusa dal perimetro FLMNDE è zona di sterro mentre la parte rimanente è zona di riporto.
Per calco1are il volume di sterro si considerano i sei prismi triangolari con la faccia inferiore
orizzontale a quota H e con la faccia superiore costituita, rispettivamente, dai triangoli FPL, LPM,
MPN, NPD, DPE, EPF. Considerando che gli spigoli, coincidono con le quote rosse dei vertici,
indicando con S1, S2 ,S3 , S4, S5, S6 , le proiezioni orizzontali dei suddetti triangoli e non considerando
le quote rosse nulle, per le note proprietà dei solidi prismatici a base triangolare i volumi saranno
calcolati con le seguenti formule:
V1 = S1
hP + hF + hL
h
= S1 P ;
3
3
V4 = S 4
hP + h N + hD
h
= S4 P ;
3
3
V2 = S 2
V5 = S 5
hP + hL + hM
h
= S2 P ;
3
3
hP + hE + hD
h +h
= S5 P E ;
3
3
V3 = S 3
V6 = S 6
hP + hM + hN
h
= S3 P ;
3
3
hP + hE + hF
h +h
= S6 P E ;
3
3
cioè:
V6 = (S1 + S 2 + S 3 + S 4 )
hP
h +h
+ (S 5 + S 6 ) P E
3
3
Per calcolare il volume di riporto si considerano i due prismi triangolari e i quadrangolari (flg. 2),
tutti con la faccia superiore orizzontale e con quella inferiore costituita, rispettivamente, dai
triangoli AFL, CDN e dai quadrilateri ABLM, BCMN. I prismi quadrangolari si devono dividere,
ciascuno, in due prismi triango1ari mediante piani verticali diagonali le cui tracce sono BL e BN.
Indicando con on S’1, S’2, S’3, S’4, S’5, S’6 le aree delle proiezioni orizzontali, rispettivamente, dei
triangoli FAL, ABL, BML, BNM, BCN, CDN e non considerando le quote rosse nulle, per le note
proprietà dei solidi prismatici a base triangolare i volumi saranno calcolati con le seguenti formule::
V '1 = S '1
hF + h A + hL
h
= S '1 A
3
3
V '3 = S '3
hB + hM + hL
h
= S '3 B
3
3
V '4 = S '4
hB + hN + hM
h
= S '4 B
3
3
hB + hC + hN
h +h
= S '5 B C
3
3
V '6 = S '6
hC + hD + hN
h
= S '6 C
3
3
V ' 5 = S '5
V '2 = S '2
h A + hB + hL
h +h
= S '2 A B
3
3
Pertanto il volume totale di riporto è dato dall’espressione:
Vr = S '1
h +h
h
hA
h +h
h
h
+ S ' 2 A B + S '3 B + S ' 4 B + S '5 B C + S ' 6 C
3
3
3
3
3
3
se risulta Vs > Vr nell’esecuzione dello spianamento si ha un eccesso di scavo e quindi occorre
portare terra a rifiuto.
Se risulta Vs < Vr si ha uno spianamento con eccesso di riporto e quindi occorre prendere del terreno
da cave di prestito.
La presenza di quote rosse sia positive che negative è dovuta al tatto che la quota del piano di
progetto è intermedia tra le quote dei vertici della superficie topografica. In questo caso lo
spianamento viene realizzato effettuando sia scavi che riporti.
Se la quota del piano di progetto è maggiore o minore delle quote di tutti i vertici della superficie
topografica, si ha rispettivamente uno spianamento di solo riporto o con soli scavi. Nel primo caso
le quote rosse sono solo positive mentre nel secondo sono tutte negative. In entrambi i casi non si
hanno punti di passaggio e quindi la risoluzione analitica risulta notevolmente semplificata
soprattutto nel calcolo dei volumi che sono di solo riporto o di solo scavo.
1. Spianamento con un piano passante per tre punti assegnati.
2. Spianamento con un piano passante per due punti noti ed avente pendenza assegnata.
Per definire analiticamente le varie fasi, che sono state precedentemente riportate, si rimanda
alla trattazione riportata sul libro di testo che riprende i principi fondamentali della geometria
solidità applicata al caso specifico.