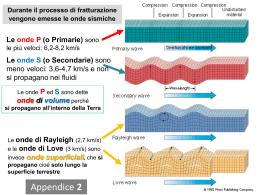
ONDE SUPERFICIALI
Alla superficie libera di un mezzo elastico si realizzano condizioni particolari nel
campo di sforzi, essendo nulli gli sforzi di taglio. Nel caso della Terra, dal momento
che le misure sismiche vengono fatte alla sua superficie, è importante considerare gli
effetti della superficie libera.
Alla superficie coesistono, simultaneamente, sia onde incidenti che onde riflesse, ed
il moto totale implica la somma delle loro ampiezze.
L’interazione delle onde P e SV alla superficie libera dà luogo alla genesi delle onde
di Rayleigh che viaggiano lungo la superficie della Terra
La riflessione totale delle onde SH alla superficie, in presenza di stratificazione
superficiale, dà luogo alla genesi delle onde di Love che si propagano
orizzontalmente lungo la superficie.
Proprietà delle onde superficiali:
•
la loro velocità di propagazione è minore di quella delle onde S
•
la loro ampiezza diminuisce in funzione della radice quadrata della
distanza dalla sorgente
onde superficiali
S
r
AS ∝
fronte d'onda
•
1
x
onde di volume
nel caso di un mezzo stratificato danno luogo al fenomeno della
dispersione, cioè la velocità di propagazione è funzione della frequenza
ONDE DI RAYLEIGH
Implicano l’interazione di onde P e SV alla superficie libera:
x3 = 0
σ 13 = σ
12
=0
Consideriamo due casi di onde P e SV incidenti su una superficie libera, che si
propagano nel piano x1-x3 :
1
2
x1
j1 j2
i 1 i2
j2
α, β, π
SVRifl
x3
α, β, π
i2
PRifl
SVRifl
PRifl
PI
x1
SVI
x3
Poiché α > β, esiste un angolo di incidenza per le onde SV definito critico:
j = jc = sin −1 (β α )
tale che le onde P riflesse viaggiano lungo la superficie libera (i2 = 90°).
Per angoli di incidenza j > jc vengono generate onde evanescenti, con ampiezza che
decade esponenzialmente con x3.
PRifl
SVI
jc
j2
x1
x1
SV
P
α, β, π
i2
SVRifl
x3
x3
L’esistenza simultanea di onde evanescenti P e SV dà luogo ad un nuovo tipo di
onde, definite onde di Rayleigh.
Lo spostamento che imprime al mezzo la propagazione di onde di Rayleigh è dato
dalle componenti:
(
u1 = − Ak sin(kx1 − ωt ) ⋅ e − 0.85kx3 − 0.58e − 0.39 kx3
(
)
u31 = − Ak cos(kx1 − ωt ) ⋅ 0.85e− 0.85kx3 − 1.47e− 0.39kx3
(1a)
)
(1b)
Lo spostamento risulta, dunque, dipendere armonicamente da x1 ed
esponenzialmenteda x3. Gli spostamenti x1 e x3 sono sfasati di 90°, e perciò si
combinano insieme per dare un moto delle particelle di tipo ellittico e retrogrado.
In superficie, x3 = 0:
u1 = −0.42 Ak sin(kx1 − ωt )
(2a)
u3 = 0.62Ak cos(kx1 − ω t)
(2b)
C
kx1-ωt = -π
B
D
kx1-ωt = -3π/2
kx1-ωt = -π/2
kx1-ωt = -2π E A
kx1-ωt = 0
u1,u3
1
0.5
E
−2π
D
A
C
−π
0
π
B
2π
(kx1-ωt)
-0.5
-1
Le ampiezze dello spostamento generato dalle onde di Rayleigh hanno una
dipendenza esponenziale da x3 e k del tipo:
A ∝ e −Ckx 3 ∝ e − 2πCx 3
λ
in cui:
C = costante
k =
ω
c
=
2π
λ
Pertanto si verifica che lunghezze d’onda maggiori producono maggiori spostamenti
a maggiori profondità, rispetto a quanto si verifichi nel caso di piccole lunghezze
d’onda:
A
1
λ grande
λ piccolo
0
x3
Il moto impartito dalle onde di Rayleigh al mezzo ha ampiezza che decresce con la
profondità.
La distanza orizzontale tra due punti che si trovano ad avere lo stesso spostamento
durante il ciclo eclittico è definita lunghezza d’onda delle onde di Rayleigh (λ).
λ
direzione di propagazione
La velocità di propagazione delle onde di Rayleigh (c), nel caso di in solido di
Poisson (λ = µ) è pari a:
c = 0.91β
ONDE DI LOVE
Si generano in presenza di uno strato di spessore H sovrastante un semispazio, con
velocità delle onde sismiche crescente con la profondità. Lo strato forma una guida
d’onda in cui le onde SH vengono “intrappolate” a seguito di riflessioni multiple in
uno strato lento, per onde SH incidenti con angolo di incidenza maggiore o uguale
dell’angolo critico (j1 ≥ jc).
x1
SHI
SHRIFL
j1 j 2
j3
SHT
H
µ1, β1
µ2, β2
x3
per:
β1 < β2
j1 ≥ jc
l’energia delle onde SH è totalmente riflessa, all’interfaccia e alla superficie. Le onde
con incidenza post-critica vengono, dunque, “intrappolate” nello strato. In tali
condizioni vengono generate le onde di Love.
Le onde di Love sono caratterizzate da una velocità di propagazione c, che dipende
dalla frequenza.
La equazione di dispersione è così definita:
c2
µ2 1 − 2
2
⎛
⎞
β2
c
⎟ =
tan ⎜ Hk
−
1
⎜
⎟
β12
c2
⎝
⎠
µ1 2 − 1
β1
in cui:
H = spessore dello strato
c = velocità di propagazione dell’onda di Love
dall’equazione di dispersione si ottiene:
T=∞
T=0
→ c = β2
→ c = β1
(da Stein & Wysession, 2003)
(1)
Onde con periodo differente viaggiano con velocità differente. Ciò significa che il
segnale sismico si “estende” nel tempo, all’aumentare della distanza ipocentrostazione.
Modi delle onde di Love
Per dedurre la forma della curva di dispersione nella equazione (1) si è posto che
l’argomento della tangente variasse tra 0 e π/2.
La funzione tangente può assumere valori positivi per una serie infinita di intervalli
del suo argomento:
0 - π/2
π - 3π/2
2π - 5π/2
Per ciascuno di questi intervalli è possibile calcolare una funzione di dispersione,
ottenendosi, per un fissato spessore H, una famiglia di curve.
Ciascuna di tali curve corrisponde ad un modo di propagazione, corrispondendo il
primo intervallo al modo fondamentale (MF) e gli altri intervalli ai modi superiori
c
β2
MF
1MF 2MF 4MF
β1
k1 k2
k4
k