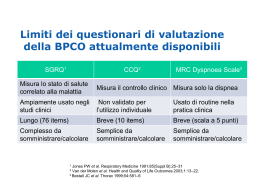
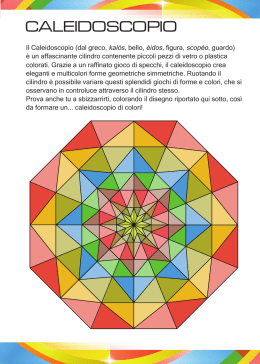
11° Incontro Internazionale sul
Rally Matematico Transalpino
RALLY- RICERCA:
ANDATA E RITORNO
FORTE DI BARD- VALLE D’AOSTA
19 – 20 – 21 ottobre 2007
RMT
fra pratica e ricerca in
didattica della
matematica
...che tipo di ricerca?
RICERCA AZIONE
• C’è qualcosa che mi rende perplesso, che
mi sbalordisce o che mi irrita in rapporto al
mio insegnamento o all’apprendimento dei
miei allievi?
• C’è una differenza fra quello che credo di
fare e quello che veramente faccio?
• Cos’è che faccio in concreto nella mia
classe?
• E’ un problema? Se sì, c’è qualcosa che
posso o dovrei fare per risolverlo?
Nunan (1989)
“studio sistematico dei tentativi
intrapresi dai gruppi dei
partecipanti per cambiare e
migliorare la prassi educativa sia
attraverso le loro azioni pratiche
sia attraverso la loro riflessione
sugli effetti di queste azioni”
Ebbutt(’85)
• In un progetto di ricerca
azione l’insegnante stesso
è l’artefice del lavoro di
ricerca
Carmel Mary COONAN
• ...perchè si possa parlare di
ricerca azione l’insegnante
dovrà impostare un
percorso di lavoro ...
articolato in fasi, tempi, ed
obiettivi da raggiungere
Carmel Mary COONAN
•
•
•
•
•
•
•
•
•
Idea iniziale.
Ricognizione.
Piano generale suddiviso in fasi.
Attuazione.
Prima valutazione.
Revisione del piano.
Nuova suddivisione in fasi.
Attuazione.
Valutazione
S. Kemmis in J. Eliot
•... la ricerca azione si
definisce più un lavoro
interpretativo e qualitativo che
psicometrico quantitativo che
punta più a scrutare processi
che a valutare prodotti; ...
Carmel Mary COONAN
I gruppi di lavoro permanenti sui
concetti in seno al RALLYE
lavorano già secondo queste
modalità
Il RALLYE è già
immerso nella
RICERCA AZIONE
•Si vedano gli
Atti di
Arco di Trento 2005
e quelli di
Parma 2006
IL RALLYE VIVE DI PROBLEMI
“Ciascuna sezione deve
obbligatoriamente fornire almeno tre
problemi (per le sezioni
piccole, ma molto piccole, ci si
accontenterà di due soli problemi,
oppure
uno solo con certificato medico!)” C.I.
INVENTARE DEI PROBLEMI!
SÌ, MA COME FARE?
NON SONO UNA MATEMATICA
NON SONO UNA RICERCATRICE
...ma il lavoro in classe è
una fonte infinita di
osservazioni
• Le domande che si pone
un insegnante sono le
stesse che sono alla
base di una ricerca
azione
•Il Rallye fornisce un
modello su come
affrontare i concetti in
classe
Problemi che sono nati dal
lavoro di classe:
•Il paese di legno
•Una sull’altra
•Caleidoscopio 1
•Caleidoscopio 2
Angoli decapitati
Poveri angoli, sono stati decapitati!
Prendine uno, incollalo sul tuo quaderno e
disegna la parte che è stata tagliata via.
Recupera poi il pezzo mancante ed incollalo
al suo posto. Scrivi le tue osservazioni.
•Osservazioni: ho
fatto una riga che
arrivava fino al
centro del triangolo
perché pensavo
potesse essere
giusta. È un po’ più
grande rispetto al
giusto, di mezzo
quadretto.
•Sono riuscito a
fare il lavoro
perché coincide ed
è uguale come
prima che si
tagliasse
•All’inizio ho
tracciato 2 linee
rette, cercando di
farle incrociare in
alto.
Non sono stato
preciso perché a
una riga li ho fatto
fare una curva
•Sì, sono riuscito a farlo
perché: appoggiando il righello
prima su di una semiretta e poi
sull’altra e continuandole, il
punto di incrocio non cambia,
per il fatto che non si spostano
e di conseguenza puntano
sempre nella stessa direzione,
formando così sempre lo
stesso e identico angolo.
•Sono riuscita a formare
l’angolo perché: prima di tutto
ho messo il righello su un lato
e ho tirato la riga mancante,
poi ho fatto la stessa cosa
dall’altra parte. I 2 segmenti si
sono incontrati e ho
cancellato il resto della riga.
• In classe il materiale può
essere preparato
dall’insegnante. La sua
distribuzione rende il
problema autovalidante.
• Problema per il Rallye:
stessa difficoltà, ma il
contesto deve essere alla
portata di tutti e il materiale
gestibile completamente
dagli alunni.
Il paese di legno (Cat. 4, 5)
Dario sta costruendo un paese di legno di 7 case con i pezzi di un
gioco di costruzioni.
Le case sono tutte diverse tra loro, ma ciascuna ha un tetto a
forma di triangolo.
Ogni tetto è formato da tre pezzi: una punta, una base e un pezzo
di mezzo.
Dario ha già costruito interamente le case 1 e 2. Sulle case 3, 4 e
5 ha messo solamente la base del tetto. Il suo fratellino gioca con
alcuni pezzi, a Dario restano le punte delle case 3, 4, 5, 6 e 7.
Qual è la punta della casa 3? e della casa 4? e della casa 5?
Spiegate come avete fatto ad individuarle.
c
a
b
d
e
punta
pezzo di mezzo
base
2
1
3
4
5
6
7
•Per trovare le punte delle casette abbiamo tirato delle righe a
partire dalle basi del tetto delle casette. Dopo abbiamo provato,
nel punto dove le linee si incrociavano, a incastrare le punte che
avevano dato. Lo spazio rimasto libero era il pezzo di mezzo.
Nessun disegno, ma questa
spiegazione
• Abbiamo trovato la punta della casa 3
misurando la base del triangolo e della
casa, ed erano di misura uguale, la punta
è la A. La punta della 5 l’abbiamo trovata
girando la punta e misurando il lato
opposto, la punta è la B.
• In una classe 4° tutti i
gruppi risolvono
correttamente, ma...
...quando riportano il lavoro
sul quaderno, 4 bambini su
18 disegnano i lati con linee
spezzate!
La Dama danzante
Caleidoscopio
•Avete 4 tesserine trasparenti con sopra sempre
lo stesso disegno.Sovrapponendole si ottengono
dei disegni diversi. Riproducete i disegni che
siete riusciti ad ottenere e scrivete con quante
tesserine li avete fatti e come devono essere
messe.
•14. UNA SULL’ALTRA (Cat. 7, 8)
Priscilla gioca con delle tesserine trasparenti sulle quali ha
disegnato una figura. Ha scoperto che sovrapponendole, si
creano nuove figure.
Sovrapponendo 4 tesserine, con
la stessa figura (a sinistra) composta
di due segmenti, si ottiene
la figura di destra:
Priscilla prova con altre 4 tesserine che hanno un altro disegno,
ottenuto tracciando tre segmenti, e ottiene
la figura qui a a fianco.
Qual è il disegno, composto da tre segmenti, che
è necessario fare sulle tesserine per poter ottenere l'ultima
figura? Esistono più soluzioni?
Spiegate la vostra risposta.
10. CALEIDOSCOPIO I (CAT. 6, 7)
Si hanno a disposizione 2 tessere quadrate trasparenti.
Su ciascuna di esse sono disegnati, come
mostra la figura qui a fianco, una quadrettatura
ed un triangolo (che si vedono da una parte e
dall’altra per la trasparenza della tessera). Se si
sovrappongono le 2 tessere facendo coincidere
perfettamente i bordi, si può ottenere, ad
esempio, questa figura che non ha assi di
simmetria:
Sovrapponendo ancora perfettamente le 2 tessere,
quante figure diverse, ma con un asse di simmetria,
si possono ottenere?
Disegnate tutte le figure diverse, con un asse di
simmetria, che avete trovato.
Caleidoscopio II ( cat. 8, 9)
•Si hanno a disposizione 4 tessere quadrate trasparenti. Su
ciascuna di esse sono disegnati, come mostra la figura qui
sotto, una quadrettatura ed un triangolo (che si vedono da una
parte e dall'altra per la trasparenza della tessera).
•Se si sovrappongono perfettamente le quattro tessere facendo
coincidere i bordi, in modo che nessuno dei quattro triangoli
coincida con gli altri, si può ad esempio ottenere la figura qui a
fianco, che non ha assi di simmetria.
•Sovrapponendo ancora le 4 tessere, quante figure diverse,
composte da quattro triangoli distinti , e con almeno un asse di
simmetria si possono ottenere?
Disegnate tutte le figure diverse che avete trovato, con quattro
triangoli distinti e almeno un asse di simmetria.
Caleidos.1
•
•
•
•
•
•
•
•
•
cat. 6
Belgio
1,23
Genova 0,43
Parma
0,87
Siena
0,39
Puglia
0,44
Milano
1,92
Franche C.1,00
Ticino
1,65
Cagliari 0,50
cat 7 Cal.2
1,17
1.54
0,63
1,70
1,75
1,71
2,36
0,45
cat 8 cat 9
0,94
0,46
0,56
1,11
0,60
0,59
0,56
0,69
0,73
0,09
• Il Rallye offre una vasta
gamma di problemi da
provare, discutere,
analizzare, per apprendere
la matematica in modo
coinvolgente e motivante.
• L’insegnante utilizza il
Rallye e ad esso ritorna,
portando la propria
competenza, il proprio
desiderio di collaborare e di
apprendere, attraverso
l’elaborazione di nuovi
problemi.
Rallye – lavoro di classe:
andata e ritorno
in uno scambio dinamico e
arricchente