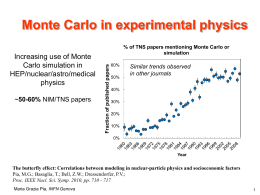
Epistemic and systematic uncertainties
in Monte Carlo simulation:
an investigation in proton Bragg peak simulation
Maria Grazia Pia
INFN Genova, Italy
Maria Grazia Pia1, Marcia Begalli2, Anton Lechner3, Lina Quintieri4, Paolo Saracco1
1 INFN
Sezione di Genova, Italy
2 State University Rio de Janeiro, Brazil
3 Vienna University of Technology, Austria
4 INFN Laboratori Nazionali di Frascati,, Italy
SNA + MC 2010
Joint International Conference on
Supercomputing in Nuclear Applications + Monte Carlo 2010
Maria Grazia Pia, INFN Genova
Quantifying the unknown
in Monte Carlo simulation
Maria Grazia Pia
INFN Genova, Italy
Maria Grazia Pia1, Marcia Begalli2, Anton Lechner3, Lina Quintieri4, Paolo Saracco1
1 INFN
Sezione di Genova, Italy
2 State University Rio de Janeiro, Brazil
3 Vienna University of Technology, Austria
4 INFN Laboratori Nazionali di Frascati,, Italy
SNA + MC 2010
Joint International Conference on
Supercomputing in Nuclear Applications + Monte Carlo 2010
Maria Grazia Pia, INFN Genova
Epistemic uncertainties
Epistemic uncertainties originate from lack of knowledge
Relatively scarce attention so far in Monte Carlo simulation
Studies in deterministic simulation (especially for critical applications)
Possible sources in Monte Carlo simulation
incomplete understanding of fundamental physics processes, or
practical inability to treat them thoroughly
non-existent or conflicting experimental data for a physical
parameter or model
applying a physics model beyond the experimental conditions in
which its validity has been demonstrated
Epistemic uncertainties affect the reliability of simulation results
Can we quantify them?
Maria Grazia Pia, INFN Genova
Uncertainty quantification
Epistemic uncertainties are difficult to quantify
due to their intrinsic nature
No generally accepted method of measuring epistemic
uncertainties
and their contributions to reliability estimation
Various formalisms developed in the field of deterministic
simulation
Interval analysis
Dempster-Shafer theory of evidence
Not always directly applicable in Monte Carlo simulation
Adapt, reinterpret, reformulate existing formalisms
Develop new ones specific to Monte Carlo simulation
Maria Grazia Pia, INFN Genova
Benefits of quantifying uncertainties
Epistemic uncertainties are reducible
Can be reduced or suppressed by extending knowledge
New experimental measurements
Uncertainty quantification gives us guidance about
What to measure
What experimental precision is needed/adequate
Priorities: which uncertainties generate the worst systematic effects
Measurements are not always practically possible
Uncertainty quantification to control systematics
Maria Grazia Pia, INFN Genova
Warm-up exercise
Epistemic uncertainties quantification in
proton depth dose simulation
simplicity
Maria Grazia Pia, INFN Genova
complexity
Ingredients
p stopping powers
Water ionisation potential
d-ray production
Multiple scattering
Nuclear elastic
Nuclear inelastic
Cross sections
Preequilibrium
Deexcitation
Intranuclear cascade
Maria Grazia Pia, INFN Genova
EGS5, EGSnrc
Penelope
MCNP(X)
PHITS
SHIELD-HIT
FLUKA
GEANT 3
SPAR, CALOR, CEM, LAHET, INUCL,
GHEISHA, Liège INCL, Bertini
d-ray or no d-ray
Preequilibrium or no preequilibrium
Weisskopf-Ewing or Weisskopf-Ewing
Griffin-exciton or hybrid
etc.
Geant4 physics options
Water ionization potential set through the public interface of G4Material
Maria Grazia Pia, INFN Genova
“Validation” in the literature
Beam energy (and energy spread) is not usually known
with adequate precision in therapeutical beam lines
What matters in clinical applications is the range
Typical procedure: optimize the beam parameters to be
used in the simulation by fitting them to experimental data
Determine beam energy, energy spread etc.
Use optimized beam parameter values in the simulation
This is a calibration
This is NOT validation
Maria Grazia Pia, INFN Genova
T. G. Trucano, L. P. Swiler, T. Igusa, W. L. Oberkampf, and M. Pilch,
“Calibration, validation, and sensitivity analysis: What’s what”,
Reliab. Eng. Syst. Safety, vol. 91, no. 10-11, pp. 1331-1357, 2006.
Simulation environment
Realistic proton beam line
Geometry from Geant4 hadrontherapy advanced example
G. A. P. Cirrone, G. Cuttone, S. Guatelli, S. Lo Nigro, B. Mascialino, M. G. Pia, L. Raffaele,
G. Russo, M. G. Sabini,“Implementation of a New Monte Carlo GEANT4 Simulation Tool for the
Development of a Proton Therapy Beam Line and Verification of the Related Dose Distributions”,
IEEE Trans. Nucl. Sci., vol. 52, no. 1, pp. 262-265, 2005
Water sensitive volume, longitudinal 200 mm slices
(through G4ReadoutGeometry)
Proton beam: E = 63.95 MeV, sE = 300 keV
Physics modeling options configured through an
application design based on G4VModularPhysicsList
1 million primary protons
Geant4 8.1p02, 9.1(ref-04), 9.2p03, 9.3
Maria Grazia Pia, INFN Genova
Reference physics configuration
Wellisch & Axen
Wellisch & Axen
Maria Grazia Pia, INFN Genova
General features
electromagnetic
electromagnetic + hadronic elastic
electromagnetic + hadronic elastic +
hadronic inelastic
59.823 MeV peak
s=376 keV
Maria Grazia Pia, INFN Genova
electrons
Water mean ionisation potential
Ep = 63.95 MeV
I = 75 eV, 67.2 eV, 80.8 eV
Ep = 63.65 MeV (1s from 63.95 MeV)
I = 80.8 eV
GoF tests Bragg-Bragg
p-value = 1
(Kolmogorov-Smirnov, Anderson-Darling, Cramer-von Mises)
Maria Grazia Pia, INFN Genova
Proton stopping powers
ICRU49
Ziegler77
Ziegler85
Ziegler2000
Differences would be masked by typical
calibration of simulation input parameters
Maria Grazia Pia, INFN Genova
Hadronic
elastic
scattering
U-elastic
Bertini-elastic
LEP (GHEISHA-like)
CHIPS-elastic
Wald-Wolfowitz test:
p-value< 0.001
p-value (reference: U-elastic)
Bertini
LEP
CHIPS
Maria Grazia Pia, INFN Genova
Difference of
deposited
energy in
longitudinal
slices
Hadronic inelastic cross sections
GHEISHA-like
Wellisch & Axen
Difference of
deposited energy
in longitudinal
slices
Bragg peak profiles
p-value > 0.9
(Kolmogorov-Smirnov,
Anderson-Darling,
Cramer-von Mises)
99% confidence interval for inelastic scattering occurrences in water
(Wellisch & Axen cross sections): 1688-1849
Occurrences with GHEISHA-like cross sections: 1654
Maria Grazia Pia, INFN Genova
Hadronic inelastic scattering models
No visible difference in
Bragg peak profiles
Wald-Wolfowitz test
p-value< 0.001
for all model options
except
p-value=0.360
for Liège cascade
preequilibrium =
no preequilibrium
Maria Grazia Pia, INFN Genova
p-value (reference: Precompound)
Hadronic inelastic
differences
reference: Precompound
Bertini
LEP
Liège
CHIPS
Difference of
deposited
energy in
longitudinal
slices
secondary p
Precompound
Bertini
LEP
Liège
CHIPS
secondary n
Precompound
Bertini
LEP
Liège
CHIPS
Wald-Wolfowitz test: p-value < 0.001
Maria Grazia Pia, INFN Genova
reference: default Evaporation
Nuclear
deexcitation
GEM
evaporation
Geant4 < 9.3
(bug fix)
default evaporation
GEM evaporation
Fermi break up
Binary Cascade
Fermi
break-up
Maria Grazia Pia, INFN Genova
Difference of
deposited
energy in
longitudinal
slices
Difference of
deposited
energy in
longitudinal
slices
Cascade-preequilibrium
Precompound model activated through Binary Cascade
w.r.t. standalone Precompound model
Difference of
deposited
energy in
longitudinal
slices
systematic
effect
Maria Grazia Pia, INFN Genova
Transition between
intranuclear cascade and
preequilibrium determined by
empirical considerations
In Geant4 Binary Cascade
model cascading continues
as long as there are
particles above a 70 MeV
kinetic energy threshold
(along with other conditions
required by the algorithm)
Some get lost on the way…
4.8
4.7
95%
confidence
intervals
Acceptance (%)
4.6
4.5
4.4
4.3
4.2
4.1
4.0
3.9
8.1
July
2006
9.1
9.2.p03
9.3
Geant4 version
9.3
hMS
December
2009
Calibration: 50 and 200 GeV
Maria Grazia Pia, INFN Genova
Multiple scattering
8.1
9.1
9.2p0.3
9.3
9.3 hMS
RangeFactor
StepLimit
0.02
0.02
0.02
0.04
0.2
1
1
1
1
0
G4hMultipleScattering, Geant4 9.3
G4MultipleScattering, Geant4 9.3
G4MultipleScattering, Geant4 9.2p03
G4MultipleScattering, Geant4 9.1
G4MultipleScattering, Geant4 8.1p02
Maria Grazia Pia, INFN Genova
LatDisplacement
1
1
1
1
G4MultipleScattering
G4hMultipleScattering
skin
0
3
3
3
geomFactor
2.5
2.5
2.5
2.5
Model
UrbanMSC
UrbanMSC
UrbanMSC
UrbanMsc92
UrbanMsc90
Reference:
Geant4 9.3 G4hMultipleScattering
Difference: G4MultipleScattering in Geant4
9.3 9.1 9.2p03 8.1p02
Difference of
deposited
energy in
longitudinal
slices
Goodness-of-fit
Maria Grazia Pia, INFN Genova
99.9% CI
Total deposited energy
2800
9.3 hMS
Total deposited energy (GeV)
2700
9.3
9.2p03
9.1
8.1p02
Dec.
2009
2600
2500
2400
9.3 hMS
Feb.
2010
8.1p02
Dec.
2007
2300
99.9% CI
2006
2200
8.1.p01 Jul
2006
9.1 Dec 2007
9.2.p03 Feb
2010
9.3 Dec 2009 9.3 hMS Dec
2009
9.3 hMS
Geant4 version
9.3
9.2p03
9.1
8.1p02
Acceptance
Maria Grazia Pia, INFN Genova
fresh from the oven…
M.G.Pia, M. Begalli, A. Lechner,
L. Quintieri, P. Saracco
Physics-related
epistemic uncertainties
in proton
depth dose simulation
IEEE Trans. Nucl. Sci., vol.
57, no. 5, pp. 2805-2830,
October 2010
Maria Grazia Pia, INFN Genova
Conclusions
Evaluation of systematic effects associated with
The impact of epistemic
epistemic uncertainties
Sensitivity analysis (~interval analysis)
More refined methods: Dempster-Shafer
Methods specific to Monte Carlo simulation?
uncertainties depends on
the experimental
application environment
Complementary statistical methods contribute to
identify and quantify effects
Qualitative appraisal is not adequate
Epistemic uncertainties are reducible
Can be reduced or suppressed by extending knowledge
New experimental measurements
Uncertainty quantification gives us guidance about
What to measure
What experimental precision is needed/adequate
Priorities: which uncertainties generate the worst systematic effects
Maria Grazia Pia, INFN Genova
Backup
100 GeV mu+, 1 m Fe, lateral deviation at end-point
1450
1350
Deviation (microm)
1250
1150
1050
950
850
750
650
550
Geant4 version
Geant4/examples/extended/electromagnetic/testEm5/mumsc/deviation.ascii
Maria Grazia Pia, INFN Genova