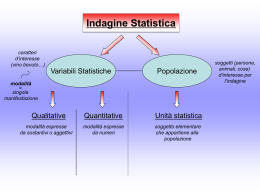
statistica
elaborare informazioni: come e soprattutto perché
alessandro polli
facoltà di scienze politiche, sociologia, comunicazione
2 marzo 2015
L'informazione non è fatta solo di notizie. È la struttura del mondo reale
C'è un modo pratico per classificare le informazioni:
• Su
Le informazioni possono essere • Per
• Come
qualcosa
Un'impronta digitale sulla scena di un delitto ci può
dire chi è l'assassino (informazione su qualcosa), può
essere utile per risolvere il caso (per qualcosa) e può
svelare la dinamica dell'omicidio (come è stato
commesso)
Luciano Floridi (2010), Information. A very short
introduction, Oxford University Press
Ma allora, che cos'è l'informazione?
L’informazione è una componente essenziale di tutto ciò che esiste: è il
mezzo attraverso il quale entriamo in contatto con la realtà esterna
«L'informazione ha un duplice aspetto. Può essere una componente
interna delle cose o essere una descrizione generale di una data tipologia
di cose» [Floridi, cit.]
Esempio
Ipotizziamo un oggetto (una t-shirt) esposto in una vetrina:
dà informazioni sul suo colore, sulla sua consistenza, sulle
finiture di quell'oggetto e, se lo compro, avrò proprio quello.
La stessa t-shirt in vendita nel Web: sul catalogo troviamo
informazioni generali, ma non su qualità come la consistenza
del singolo esemplare. E se la si compra non è proprio quella
della foto: solo una con le stesse caratteristiche
Una definizione in termini di processo di comunicazione
Informazione è un termine che ricorre spesso
nel linguaggio di tutti i giorni, ma non si presta
a definizioni univoche
Il principale ostacolo in tal senso nasce dal
fatto che questo termine è utilizzato nei
contesti più vari
Una descrizione precisa dei fenomeni in cui
interviene il concetto di informazione deve
quindi essere preceduta da un'analisi dei
fenomeni stessi, al fine di individuarne le
principali caratteristiche
Il processo di comunicazione
Il processo di comunicazione è uno schema interattivo tra
1. Una sorgente che ha la necessità o la potenzialità di
comunicare informazioni
2. Un canale (mezzo di trasmissione, media), attraverso cui il
messaggio si propaga e si diffonde
3. Un destinatario che riceve le informazioni
Il processo di comunicazione
Lo schema può essere reso più completo:
1.
La sorgente emette l’informazione utilizzando un trasmettitore
2.
Prima di inviare un messaggio lungo il canale, il trasmettitore traduce
l’informazione in forma adatta alla trasmissione. La traduzione
dell’informazione da parte del trasmettitore può essere fatta in modo tale da:
A.
proteggere l'informazione trasmessa (problema della criptatura)
B.
adeguare il linguaggio usato dalla sorgente al linguaggio del destinatario
3.
Il canale provvede al trasporto dell’informazione. In base alle proprie
caratteristiche fisiche il canale può trasportare una quantità di informazione più
o meno grande. Mentre viaggia all'interno del canale, l'informazione è
sottoposta ad una serie di fenomeni, indicati dal termine rumore, che tendono a
distorcerla
4.
Il messaggio giunge al ricevitore, che svolge le operazioni inverse a quelle svolte
dal trasmettitore e ritraduce il messaggio
5.
Il messaggio giunge al destinatario. Non sempre il messaggio in arrivo è uguale a
quello inviato originariamente
Il processo di comunicazione
All’interno di un processo di comunicazione, l’informazione è una
notizia (cioè un elemento cognitivo nuovo per il ricevente e in
quanto tale suscettibile di risolvere una condizione di incertezza)
codificata come testo scritto, discorso, sistema convenzionale di
segni, dato numerico, codice binario (bit)
In generale l’informazione è una sequenza di simboli: la sorgente
di un processo è una qualunque entità che può trasmettere
informazioni sotto forma di sequenze di simboli
Il canale è il mezzo attraverso il quale è trasmessa l'informazione
La caratteristica propria del canale è il fatto di produrre rumore (o
distorsione, o errore), una caratteristica presente in tutti i processi
di comunicazione
L’approccio in termini cognitivi
L’approccio cognitivo enfatizza le relazioni tra la realtà
fenomenica e la sua interpretazione da parte di un agente.
Congettura
Informazione
Agente
Output
Input
Controllo
Realtà
Teoria
Una teoria diffusa nell’ambito delle scienze cognitive è il c.d.
modello input/output:
Fenomeno/fatto/fenomenologia
L’uso scientifico del termine fenomeno fa riferimento ad
avvenimenti ed eventi che accadono intorno a noi (nel tempo
e nello spazio) e che siamo in grado di osservare
I «fenomeni» pertanto sono logicamente distinti dagli
«oggetti» che pure si trovano intorno a noi, ma che
mantengono nel tempo e nello spazio una sostanziale
identità
La definizione di fenomeno implica quindi un qualche tipo di
mutamento di stato nel tempo e/o nello spazio
Fenomeno/fatto/fenomenologia
Una parola spesso utilizzata come sinonimo di fenomeno è
fatto
Tuttavia l’uso di quest’ultimo termine è limitato a un singolo
evento, mentre il fenomeno indica un insieme di fatti in
qualche modo collegati tra loro
Esempio: un crollo di borsa è un fatto economico; i corsi azionari, le operazioni
di mercato, la produzione industriale sono fenomeni economici
In alcuni casi il collegamento tra fatti può essere stabilito in
maniera agevole e intuitiva attraverso l’osservazione. In altri
casi l’individuazione del legame può richiedere il passaggio
dall’osservazione all’esperimento
Fenomeno/fatto/fenomenologia
Con il termine fenomenologia indichiamo un insieme di fatti
e fenomeni posti convenzionalmente in relazione
Il mondo «reale» è caratterizzato dall’esistenza di oggetti e
dal verificarsi di processi, mutamenti, fatti e fenomeni
Le caratteristiche di «realtà» di tali elementi sono definite in
base a convenzioni, cioè ad accordi intersoggettivi tra
osservatori
L’attribuzione al fenomeno di qualificazioni quali «fisico», «biologico»,
«economico» implica sempre il riconoscimento di un contesto, di
caratteristiche comuni e, talvolta, l’esistenza di una descrizione scientifica
Dall’osservazione alla descrizione, dalla descrizione alla teoria
Nella vita di tutti i giorni siamo soliti descrivere i fenomeni
limitandoci ad evidenziarne le caratteristiche più evidenti
Queste descrizioni possono assumere il carattere di leggi
anche se sono espresse esclusivamente in forma verbale
Il problema nasce dal fatto che una descrizione verbale
potrebbe rivelarsi inadeguata in presenza di concatenazioni di
eventi particolarmente complesse, tanto da rendere
impossibili previsioni accurate
In questi casi è necessario definire meglio il fenomeno
indicando le grandezze suscettibili di misurazione e che ne
determinano l’evoluzione
Dall’osservazione alla descrizione, dalla descrizione alla teoria
I fenomeni possono essere descritti in forma parzialmente
unificata attraverso leggi empiriche, cioè relazioni tra le
grandezze che ne influenzano manifestazioni e dinamica
Il problema centrale nella descrizione scientifica di un
fenomeno risiede quindi nella definizione e misurazione di
tali grandezze, che prendono il nome di variabili
È importante notare che la descrizione di un fenomeno
attraverso leggi empiriche, fornendo indicazioni sulle sue
modalità di manifestazione, potrebbe consentirci di formulare
qualche tipo di previsione anche per fenomeni simili
Dall’osservazione alla descrizione, dalla descrizione alla teoria
Una più ampia capacità predittiva si ha tuttavia se più fenomeni
possono essere inquadrati in uno stesso schema teorico.
Una teoria, a differenza di una legge empirica, definisce un
mondo ideale che rappresenta il modello per descrivere e
spiegare i fenomeni osservati
In altri termini si elabora uno schema teorico per comprendere
perché il fenomeno ha luogo e perché si manifesta nel modo
osservato empiricamente
Dall’osservazione alla descrizione, dalla descrizione alla teoria
Gli schemi teorici sono generalmente espressi in forma di
relazioni funzionali tra variabili, il che rende necessaria l’adozione
di una notazione logico-matematica
Se il nostro obiettivo è verificarne la capacità esplicativa e
l’applicabilità nel mondo reale, tuttavia, prima o poi saremo
obbligati a “riportare la vita” nei nostri (più o meno) sofisticati
schemi teorici e sostituire quantità numeriche alle variabili
matematiche
Dall’osservazione alla descrizione, dalla descrizione alla teoria
Questo passaggio dall’astrazione teorica alla realtà non è
immediato come potrebbe sembrare
L’analisi di situazioni concrete richiede che queste ultime possano
essere individuate, definite e misurate
Possiamo svolgere queste operazioni su un fenomeno
considerato nella sua globalità o, più spesso, su un sottoinsieme
ristretto di sue manifestazioni, spesso individuate tramite
procedure di campionamento
Va notato che a differenza delle scienze sperimentali,
in cui l’esperimento può entro certi limiti essere
ripetuto, nelle scienze sociali la possibilità di
effettuare esperimenti in condizioni di laboratorio
rappresenta un’eccezione e non la regola
Organizzare e analizzare le informazioni
Formulare congetture, teorie, previsioni sul mondo circostante è
un’attività abituale dell’essere umano e non è confinata agli
operatori della conoscenza
L’essere umano è posto nella necessità di interpretare fatti e
fenomeni e risalire a concatenazione casuali che possono essere
molto complesse
In tale attività conoscitiva assume centralità il processo di
organizzazione e analisi delle informazioni raccolte
L’organizzazione e l’analisi delle informazioni è uno degli
obiettivi delle discipline statistiche
Breve storia delle discipline statistiche
La statistica nella sua evoluzione non si discosta dal percorso di
altre discipline scientifiche: nasce come attività pratica,
indirizzata alla soluzione di problemi concreti e contingenti, per
poi sistematizzarsi in una successiva fase metologica
In quanto disciplina scientifica, la statistica è relativamente
recente: le prime attività ad essa riconducibili risalgono al XVII
secolo e furono favorite dal grande sviluppo delle discipline
matematiche e del c.d. metodo scientifico
La pratica statistica nell’antichità
La pratica statistica si è sviluppata in epoche lontane. Ancora
prima che si evolvesse la scrittura, l’uomo incideva tacche al fine
di contare uomini, prodotti della caccia, animali allevati (cioè
forme elementari di censimento e di inventario)
Tali attività possono essere considerate le prime rudimentali
statistiche (intese come descrizione quantitativa di fenomeni di
interesse), nate dalla necessità di conoscere gli elementi rilevanti
dell’habitat esterno all’osservatore
La pratica statistica nell’antichità
Tracce di tali attività originarie sono evidenti nei sistemi numerici
in uso nell’antichità:
Sistema numerico
sumero
Sistema numerico
babilonese
Sistema numerico
egizio
La pratica statistica nell’antichità
Con l’affermazione delle prime grandi civiltà (cinese, babilonese,
egizia) nasce l’esigenza di raccogliere informazioni e sintetizzarle
attraverso semplici elaborazioni statistiche
La finalità prevalente delle rilevazioni pratiche è sempre stata
quella di reperire dati ed elementi per consentire il miglior
governo della cosa pubblica. In particolare, l’obiettivo di tali
rilevazioni era costituito dalla raccolta di informazioni su
•
•
•
•
la popolazione nel suo complesso;
gli uomini idonei alle armi;
la determinazione del gettito delle imposte;
la ripartizione della proprietà terriera
Breve excursus delle rilevazioni statistiche svolte nell’antichità
Cina. L’impero cinese era caratterizzato da una popolazione numerosa e da
un vasto territorio. Era quindi fondamentale, per i suoi governanti,
conoscere la numerosità dei sudditi e l’estensione dell’impero
La fonte documentale di tali attività è uno dei testi sacri del confucianesimo,
lo Shu-King, che narra come, nel 2200 a.C., dopo una grave inondazione, il
ministro Yu dell’imperatore Yao, per conoscere i confini dell’impero e per
richiedere i tributi:
•
•
•
•
divide il territorio della Cina in 9 province;
ne misura l’estensione;
individua le produzioni economicamente rilevanti;
censisce la popolazione, classificandola per attività e mestieri esercitati
Successivamente si ha notizia di censimenti attuati circa ogni tre anni e,
durante l’epoca Ming (1368-1644), ogni dieci anni
Breve excursus delle rilevazioni statistiche svolte nell’antichità
India. Informazioni sulle pratiche statistiche realizzate in India si ricavano dal
Darmasastra, il codice civile e religioso compilato da Manu nel 1200 a.C.
Questo testo illustra le regole che «da tempo immemorabile riguardano la
condotta dei Principi», cioè quei principi di amministrazione del territorio
che presuppongono, da parte del sovrano, la conoscenza dei principali
elementi della vita economica della regione
Le rilevazioni, attuate secondo regole indicate dal testo stesso, consentivano
la disciplina delle industrie e dei commerci da parte dell’autorità statale
Breve excursus delle rilevazioni statistiche svolte nell’antichità
Antico Egitto. Le notizie che abbiamo sulle attività statistiche nell’antico
Egitto sono per lo più di fonte greca e latina (Erodoto, Diodoro,Tacito)
Da tali autori apprendiamo che a partire dal 3000 a.C. si realizzarono
censimenti della popolazione per motivi fiscali, militari ma anche per sapere
quanta manodopera era disponibile per realizzare opere pubbliche
Gli Egizi attribuirono l’esecuzione di operazioni statistiche a Sefchet (o
Safhkit o Sashet), la dea dei libri e dei conti
Breve excursus delle rilevazioni statistiche svolte nell’antichità
Mesopotamia. Presso i Sumeri sono state ritrovate tavolette di argilla in cui
sono riportate liste di uomini e di beni, quasi sicuramente compilate a fini
fiscali e risalenti al IV–III millennio a.C. Tali rilevazioni scritte sono fino ad
oggi le più antiche in nostro possesso
In Assiria, nella biblioteca del re Assurbanipal, erano custoditi documenti
statistici sulle gerarchie degli ufficiali amministrativi, sulle province
dell’impero e sulle principali produzioni di beni
Breve excursus delle rilevazioni statistiche svolte nell’antichità
Ebrei. L’unica fonte documentale è la Bibbia
(Esodo 12,37) Narra del censimento degli uomini che partirono dall’Egitto e
quello ad un anno da tale partenza. Questo censimento fu attuato da Mosè e
da Aronne che utilizzarono l’esperienza acquisita alla corte del faraone
(Numeri 1, 1-4) Riporta le modalità di tale rilevazione, i nomi dei rilevatori e gli esiti. Furono così
censiti 603.550 uomini corrispondenti ad una popolazione di circa 2.000.000 di persone
(Numeri 26, 51) Alla fine dei quarant’anni nel deserto la popolazione fu nuovamente contata, e si
trovò un totale di 601.730 uomini. Tale censimento fu compiuto al fine di individuare i soldati
disponibili per la guerra volta alla conquista del territorio d’Israele
(Samuele 24 1ss.) Racconta il censimento voluto dal re Davide
Breve excursus delle rilevazioni statistiche svolte nell’antichità
Antica Grecia. Si ha notizia del censimento di Solone, in relazione alla
riforma fiscale legata alla proprietà della terra e, in particolare, all’esigenza di
stilare una lista degli elettori basata sul valore della terra da loro posseduta
Tucidide applica semplici metodi statistici (in particolare la media aritmetica)
per risolvere alcuni semplici problemi di stima. Lo stesso storico mette poi in
guardia i lettori contro i dati riportati da Erodoto e Omero, che ritiene poco
attendibili
Gli ateniesi applicarono un sistema per rilevare nascite e morti: i parenti
avevano l’obbligo di offrire alla sacerdotessa di Minerva una misura d’orzo
(nel caso di nascita), una di frumento (in caso di morte) ed un obolo in
occasione di ogni nascita e di ogni morte. Il conteggio di tali oboli consentiva
quindi di risalire al numero dei nati e dei morti
Breve excursus delle rilevazioni statistiche svolte nell’antichità
Antica Roma. La società romana era organizzata su basi censitarie. I cittadini
erano così registrati congiuntamente ai loro beni nel «census», la radice
latina del termine «censimento»
La raccolta amministrativa di informazioni a Roma era basata sulla
rilevazione congiunta dei cittadini e dei loro beni
Ogni cittadino doveva dichiarare allo Stato
•
•
•
il proprio nome e il patronimico;
i nomi della moglie e dei figli;
l’entità dei propri beni
Tali dichiarazione erano in seguito registrate (censite) dall’amministrazione
statale. Tali registri servivano poi alla ripartizione delle imposte. A tale
compito erano preposti due «censores» - istituiti nel 443 a.C. - i più
importanti magistrati romani dopo i consoli
Le rilevazioni statistiche dal Medioevo al Rinascimento
Impero carolingio. Carlo Magno (808) istituisce nei possedimenti sottoposti
alla sua autorità il breviarium fiscalium per rilevare e aggiornare
•
•
•
l’entità e il valore delle terre poste sotto autorità imperiale;
I benefici della chiesa;
I benefici dei feudatari
Inventari dei latifondi regi e delle grandi proprietà terriere private furono poi
ordinati da Carlo il Grosso e da Lodovico il Germanico. Gli organismi
ecclesiastici quali abbazie e monasteri attivarono un «registro dei beni»
comprendente il numero degli abitanti e dei terreni ad essi soggetti, per
determinare le decime
Le rilevazioni statistiche dal Medioevo al Rinascimento
Inghilterra. In Inghilterra il re normanno Guglielmo il Conquistatore
costituisce il Doomsday-book o Domesday (1083-86) che descrive
•
•
•
•
le terre, il loro valore, il prezzo degli affitti ed i relativi proprietari;
il numero dei servi sassoni;
i mulini, gli stagni;
gli alveari, gli aratri, il bestiame
Da notare che il nome sassone domes daeg significa sia il giorno
dell’udienza, sia il giorno del giudizio
Le rilevazioni statistiche dal Medioevo al Rinascimento
Arabi. Nel periodo della loro espansione in Spagna svolsero molte rilevazioni
statistiche. Nel 702 d.C. il governatore di Cordova inviò al Califfo d’Africa una
descrizione particolareggiata
•
•
•
•
•
della geografia della Spagna;
del numero degli abitanti;
delle fabbriche, degli operai;
dei libri nelle biblioteche;
dell’ammontare delle rendite
Le rilevazioni statistiche dal Medioevo al Rinascimento
Repubblica di Venezia. La Repubblica Veneta tenta di organizzare le
informazioni necessarie al governo del territorio sin dai suoi primordi. Nel
978 la Repubblica stila un elenco delle persone soggette al pagamento delle
tasse e, nel 1171, una lista dei cittadini creditori verso lo stato (catasticus)
Nel XII secolo è istituito il registro dei forestieri e degli iscritti alle
corporazioni
Nel 1311 si svolge il censimento di Corone e Modone, città soggette al
dominio di Venezia, che costituisce il primo modello di rilevazione diretta,
nominativa e universale
Nel 1440 il Consiglio dei Dieci istituisce un piano di rilevazione che può
essere considerato il primo censimento moderno della popolazione, distinta
per età, sesso, professione, condizione sociale e nazionalità
Le rilevazioni statistiche dal Medioevo al Rinascimento
Le rilevazioni parrocchiali. Sul finire del 1400 si diffuse l’uso di compilare
«tavole genetliache» in cui venivano iscritti i nomi di tutti i battezzati, dei
loro genitori e dei padrini sia in Italia sia in Francia; furono pure introdotti i
“registri mortuari” nei quali venivano registrate le persone decedute
Il Concilio di Trento (1565) accoglie questa pratica ed obbliga i parroci alla
tenuta dei registri dei battesimi, dei matrimoni e delle morti
Anche la neonata Chiesa Anglicana, su ordine del cancelliere Thomas
Cromwell, impone ai suoi parroci, quasi contemporaneamente alla chiesa
cattolica, l’obbligo di svolgere tali rilevazioni
La nascita della statistica come metodologia
L’evoluzione delle scienze dopo Galileo coinvolge anche le rilevazioni
pratiche delle informazioni, che si avviano a diventare statistiche vere e
proprie. Difatti quando un’attività pratica diventa sempre più complessa e
frequente sorge la necessità di stabilire un metodo per la sua realizzazione.
La ricerca di un metodo proprio per la Statistica perseguì due scopi:
•
•
dare basi scientifiche alle indagini e alle rilevazioni per garantirne
l’affidabilità (la verosimiglianza)
sintetizzare in modo appropriato un insieme di dati per
identificare e leggere le caratteristiche del collettivo osservato
La nascita della statistica come metodologia
Nel XVII secolo non ci si limita più ad osservare dati di per sé “statici”, a fare
cioè pura e semplice contabilità, ma si inizia ad analizzare i dati
Da attività di conteggio, enumerazione ed anche di calcolo di semplici medie
su rilevazioni svolte per gli scopi più diversi, considerabili ancora ambito
dell’Aritmetica, si passa all’osservazione di proprietà di un insieme di dati, del
quale si cerca di studiarne i seguenti aspetti:
•
•
•
la possibilità di sintesi delle osservazioni attraverso il calcolo
di medie;
la variabilità dei dati rispetto alla media;
la dipendenza/indipendenza di due caratteri
Questo passaggio segna l’origine una nuova disciplina che verrà
successivamente denominata «statistica»
I precursori: John Graunt e William Petty
La nascita della statistica metodologica è
attribuita a John Graunt (1620-1674)
Commerciante di tessuti nominato capitano delle
milizie civiche e socio della Royal Society di
Londra, Graunt pubblicò nel 1662 la memoria
«Osservazioni naturali e politiche elencate
nell’indice seguente ed eseguite sui bollettini
della mortalità, dal capitano John Graunt,
cittadino di Londra, con riferimento al governo,
alla religione, al commercio, allo sviluppo, al
clima, alle malattie e ai vari mutamenti della città
di Londra»
I precursori: John Graunt e William Petty
Graunt utilizzò i dati pubblicati settimanalmente, e di solito letti o per pura
curiosità o per prevedere il sorgere di un’epidemia in città, e quindi prendere
le debite contromisure quali quella di rifugiarsi nelle campagne
Il scopo di Graunt era quello di ricavare da queste tavole regolarità
scientifiche, quali l’inurbamento della popolazione contadina, il legame tra
suicidio e professione, l’eccedenza delle nascite tra i due sessi
L’innovazione di Graunt consiste nell’utilizzare nelle scienze sociali oggetto
dei suoi studi, metodi logici e tecnici di tipo naturalistico, classificatorio ed
induttivo che costituiscono il primo abbozzo scientifico della Statistica
modernamente intesa
Amico di Graunt e continuatore della sua opera fu William Petty (1623-1687)
che con gli stessi metodi calcolò la popolazione di città come Londra e
Dublino, la sua crescita, la distribuzione uomini/donne, la valutazione di beni
e merci, nonché la prima stima del reddito nazionale inglese e francese
L’aritmetica politica
L’indirizzo di studi nato da Graunt e Petty fu denominato «Aritmetica
Politica», cioè «l’arte del ragionare per mezzo di cifre sulle cose aventi
attinenza col Governo» e fu caratterizzato dall’utilizzo del metodo empirico
induttivo, proprio delle scienze naturali, matematizzando i dati
dell’esperienza
Altri esponenti dell’aritmetica politica furono L. Huygens (1692-1695), de
Witt e Jan Hudde che fecero studi sulla valutazione delle rendite sulle tavole
di mortalità, speranza di vita, curva di mortalità. Anche Leibniz attuò ricerche
sulla vita media, vita probabile, popolazione stazionaria, calcolo della
fecondità.
L’aritmetica politica
L’astronomo inglese Edmond Halley (1656-1742) raccolse le tabelle di
mortalità della città di Breslavia per regolare il valore delle assicurazioni sulla
vita, fondando così la matematica assicurativa. Il suo metodo fu corretto da
Leonardo Eulero in modo tale da tener conto dell’eccesso delle nascite sulle
morti
Tra i fondatori della statistica ricordiamo anche Abraham De Moivre (16671754): matematico francese ugonotto, costretto all’esilio in Inghilterra,
sviluppa il calcolo della probabilità per sbarcare il lunario, consigliando i
giocatori d’azzardo inglesi. De Moivre pubblicò nel novembre 1733 un saggio
sulla distribuzione binomiale e sulla transizione concettuale delle colonne
dell’istogramma alla curva continua e formulò l’equazione della curva
normale
Nasce il termine «statistica»
Corning (1660-1681), professore di diritto pubblico a Gottinga, tenne un ciclo
di lezioni nelle quali descrisse ed esaminò le “cose notevoli” di uno stato
(senza dati quantitativi) e denomina la disciplina elaborata in tali corsi come
Notitia rerum publicarum o Staatskunde
Achenwell (1719-1772), anch’egli professore a Gottinga, diede una struttura
più organica alla disciplina iniziata da Corning definendo che “la conoscenza
dello Stato” di cui si occupa la nuova disciplina è quella della sua costituzione
nel presente. Tale disciplina prese il nome di Statistica universitaria
La Statistica Universitaria si configurava come descrizione, per lo più
qualitativa, dei fenomeni oggetto di studio: non era ancora volta alla ricerca
di leggi in grado di spiegare i fenomeni descritti
La statistica come disciplina autonoma
La Statistica nasce dalla confluenza della statistica universitaria tedesca e
dell’aritmetica politica inglese
A queste si aggiungono i contributi della corrente francese tramite lo
sviluppo del calcolo delle probabilità ad opera di Pascal e Fermat e l’opera
dell’architetto militare Vauban (1633-1707) che caldeggiò l’istituzione di
statistiche ufficiali e la necessità dei censimenti, svolti tramite un’articolata
modulistica
Gli strumenti concettuali e materiali che favorirono la nascita della statistica
furono la geometria analitica e l’analisi matematica, il calcolo delle
probabilità, il calcolo dei logaritmi e lo sviluppo delle prime macchine
calcolatrici, da quella di Pascal (1642) - che meccanizzava solo addizione e
sottrazione - a quelle di Morland (1625-1695) e Leibniz che erano in grado di
eseguire anche la moltiplicazione
Gli albori della statistica induttiva
Un posto a parte nella storia della statistica è occupato da Thomas Bayes
(1702-1761), uno dei precursori della statistica induttiva (o inferenziale) e
della teoria del campionamento
Nel suo saggio «Essay towards solving a Problem in the doctrine of chances»
(uscito postumo nel 1764) Bayes si preoccupò di stabilire una concordanza
tra le ipotesi enunciate a priori e le esperienze successive ed in particolare
di come queste esperienze potessero modificare l’ipotesi relativa ad una
situazione. In sostanza il Teorema di Bayes modellizza la verifica dinamica di
ipotesi e la loro correzione in funzione delle informazioni via via disponibili
La statistica nel XIX secolo
La statistica si struttura come una disciplina che offre un ampio campo
speculativo negli ambiti demografico, economico, matematico, attuariale
Notevole per lo sviluppo di questi filoni statistici il contributo matematico di
Laplace e di Gauss, legati in particolare all’uso della probabilità
Ricordiamo per la demografia il contributo di Malthus (1766-1834) che
imposta scientificamente i problemi, raccoglie personalmente documenti
demografici ed economici ed è tra i fondatori nel 1834 della Royal Statistical
Society a Londra
La statistica nel XIX secolo
Adolphe Quételet (1796-1864). Matematico ed astronomo belga, è
considerato da molti il fondatore della Statistica moderna. Egli si occupò di
calcolo delle probabilità e ne ricercò l’applicazione nel campo dei fenomeni
sociali
Nel 1846 Quételet pubblicò le «Lettres sur la théorie des probabilités
appliquée aux sciences morales et politiques», dove illustra come, in una
popolazione omogenea, i caratteri dei singoli individui si distribuiscano
secondo una curva, avente ordinate proporzionali ai successivi termini dello
sviluppo del binomio di Newton
La statistica nel XIX secolo
Già nel 1835 Quételet aveva formulato la teoria «dell’uomo medio» che
ipotizzava il tipo fisico di una popolazione ottenuto attraverso la media
aritmetica dei vari caratteri fisici dei suoi componenti
Quételet conclude che i caratteri umani si possono studiare con il calcolo
delle probabilità e che per essi vale la legge dei minimi quadrati formulata da
Gauss e Legendre per eliminare le discordanze tra le diverse misure di un
fenomeno fisico
Questa teoria era un’illusione che fu smentita dall’analisi sperimentale e
statistica delle scienze naturali; tuttavia gli studi di Quètelet posero le basi
per l’enorme sviluppo, in tutti i campi del sapere, della statistica
La statistica nel XIX secolo
Francis Galton (1822-1911). Biologo (e cugino di C.Darwin), criminologo
(propose la registrazione delle impronte digitali per individuare i delinquenti
fuggiti o recidivi) ed esploratore africano, propugnò l’introduzione di metodi
quantitativi in biologia, progettando scale di misurazione per tutte le
caratteristiche fisiche
Si occupò anche di meteorologia (suo è il termine “anticiclone” per indicare
una zona di alta pressione)
Nei suoi saggi (1886-1888), che si pongono sulla scia di Quételet, introduce
la regressione lineare e la correlazione
La statistica nel XIX secolo
Karl Pearson (1875-1936). Formula l’equazione della legge normale
multidimensionale, scopre la correlazione parziale, il test del χ² e il metodo
di costruzione di stimatori campionari noto come metodo della massima
verosomiglianza
Pearson si rende conto che esistono fenomeni che non si distribuiscono
affatto secondo la legge «normale» e pone le basi per il loro studio
Inoltre prende coscienza che se anche due variabili naturali si comportano
secondo una data funzione, ciò non prova affatto che vi sia un legame
effettivo che spieghi i relativi fenomeni
La statistica nel XIX secolo
La statistica, che agli inizi del XIX secolo si occupava ancora della raccolta e
della sistemazione dei «fatti illustranti la condizione e le risorse dello stato»,
nella prima metà del secolo amplia il proprio ambito analizzando la
condizione della popolazione, in particolare negli aspetti riguardanti la
povertà, il crimine e l’educazione
Verso la fine del secolo si strutturò come analisi e studio di fenomeni dotati
di variabilità attinenti a qualsiasi campo del sapere (botanica, agricoltura,
zoologia, medicina, fisica). Ciò avvenne grazie al fecondo periodo di studi
iniziato da Quételet e dagli altri studiosi che furono influenzati dal suo
approccio
La statistica entra nel «secolo breve»
Alla fine del XIX secolo si impone un nuovo indirizzo statistico, noto come
inferenza statistica, che ricerca metodi per ricavare da campioni di
osservazioni e da rilevazioni parziali conclusioni valide per la totalità della
popolazione oggetto di studio
In questi studi si distinse William S. Gosset (1876-1937). Chimico, lavorò
presso la fabbrica della birra Guinness a Dublino
Gosset individuò un metodo per trarre conclusioni consistenti da campioni
piccoli o addirittura piccolissimi e pubblicò i suoi studi sotto lo pseudonimo
Student (da cui la distribuzione nota come t di Student), non essendogli
permesso di firmare lavori scientifici extraprofessionali
La statistica entra nel «secolo breve»
Ronald A. Fisher (1890-1962). Matematico, astronomo e fisico. Ancora
studente, iniziò ad occuparsi di statistica, interessandosi prevalentemente
della distribuzione campionaria, della stima campionaria e della
programmazione ed interpretazione degli esperimenti
Riformulò la t di Student e costruì i metodi più comunemente usati per
l’analisi statistica, in particolare l’analisi della varianza (ANOVA) e il piano
degli esperimenti
Molti sono gli statistici di questo periodo che approfondirono e precisarono
gli strumenti ideati da Quételet, Galton, Pearson e Fisher, ma sarebbe troppo
lungo elencarli tutti. Per chi volesse approfondire questo aspetto più
propriamente tecnico rimando al testo seguente:
Sthephen M. Stigler (1990), The history of
Statistics. The Measurement of Uncertainty
before 1900, Belknap Press
Il metodo statistico
La statistica è l’insieme dei metodi logico-matematici per lo
studio quantitativo e qualitativo di un fenomeno
Tale disciplina studia i metodi attraverso i quali una realtà
fenomenica può essere sintetizzata e quindi compresa attraverso:
1. La raccolta e l’analisi di informazioni
2. La traduzione delle informazioni in dati
3. La verifica di ipotesi
La scienza statistica è comunemente suddivisa in due branche
principali:
A. statistica descrittiva
B. statistica inferenziale
L’approccio descrittivo
La statistica descrittiva è la branca della statistica che studia i
criteri di rilevazione, di classificazione e di sintesi delle
informazioni relative ad una popolazione oggetto di studio
La statistica descrittiva raccoglie le informazioni sulla
popolazione, o su una parte di essa (campione), in distribuzioni
semplici o complesse (almeno due caratteri) e le descrive
attraverso famiglie di indici: indici di posizione, indici di
variabilità, indici di forma, rapporti statistici, relazioni statistiche
I risultati ottenuti in tal modo si possono definire certi, a meno di
errori di misurazione che, se dovuti al caso, in media si annullano.
La statistica descrittiva ha come obiettivo quello di organizzare,
riassumere e presentare i dati in modo ordinato; i suoi
strumenti permettono quindi di sintetizzare i dati
L’approccio inferenziale
Inferenza: trarre conclusioni logiche a partire dai dati osservati
La statistica inferenziale ha come obiettivo quello di risalire alle
caratteristiche di una popolazione incognita, oggetto di studio,
dall’osservazione di un campione finito di sue manifestazioni, con
una possibilità di errore predeterminata dal ricercatore
Le inferenze possono riguardare il meccanismo generatore (la
legge probabilistica) del fenomeno che si osserva. La conoscenza
di tale struttura probabilistica permetterà poi di fare una
previsione (si pensi, ad esempio, che quando si afferma che
«l'inflazione il prossimo anno avrà una certa entità» ciò implica
l’esistenza di un modello dell'andamento dell'inflazione
formulato con tecniche inferenziali)
L’approccio inferenziale
La statistica inferenziale è fortemente legata alla teoria della
probabilità
Sotto questo punto di vista descrivere in termini probabilistici o
statistici un fenomeno aleatorio nel tempo, caratterizzabile
dunque da una variabile aleatoria, vuol dire descriverlo in
termini di densità di distribuzione di probabilità e dei suoi
parametri: media (o valore atteso) e varianza
La statistica inferenziale si articola poi in altri ambiti tematici, di
cui i più importanti sono la teoria della stima (stima puntuale e
stima intervallare) e la verifica (test) di ipotesi
Il concetto di grandezza
Uno dei principali ambiti di applicazione dei metodi statistici è il
confronto tra grandezze
Nell’uso corrente, il termine grandezza ha un significato intuitivo.
Tuttavia, da una rapida consultazione di un qualsiasi dizionario (il
Sabatini Coletti nel nostro caso) appare evidente che il concetto
sottostante non risulta affatto di immediata definizione
Infatti il termine grandezza può essere riferito a: 1. Dimensioni, mole di un oggetto
considerato in lunghezza, larghezza, altezza, volume (misurare la grandezza di
qualcosa; anche con riferimento a persona: un uomo di media grandezza); 2.
Eccedenza ed eccezionalità rispetto alle misure ritenute normali, anche in senso
figurato (la grandezza di Shakespeare; avere manie di grandezza: ostentare un alto
tenore di vita non adeguato alle reali possibilità finanziarie; grandezza d'animo:
magnanimità); 3. (mat., fis.) Classe di enti a ciascuno dei quali può essere assegnata
una misura; anche, la misura stessa: grandezze omogenee, commensurabili;
grandezza scalare, vettoriale
Il concetto di grandezza
Nell’ultima accezione il termine «grandezza» è indissolubilmente
legato alle operazioni di misura. Appare quindi utile aprire una
brevissima parentesi sulla sua definizione formale
Nei «Principia Mathematica» Russell e Whitehead propongono la
seguente definizione di grandezza:
esiste una certa coppia di relazioni indefinibili, maggiore o minore; queste
relazioni sono simmetriche e transitive e sono incompatibili l’una con l’altra.
Ognuna è l’inverso dell’altra nel senso che ogni volta che una è valida tra A e
B, l’altra è valida tra B e A. I termini che risultano suscettibili di queste
relazioni sono grandezze. Ogni grandezza ha una certa relazione particolare
con qualche concetto, espressa dicendo che essa è una grandezza di quel
concetto. Due grandezze che hanno questa relazione col medesimo concetto,
si dicono dello stesso genere; essere dello stesso genere è la condizione
necessaria e sufficiente per la relazione di maggiore e minore
Alfred N. Whitehead, Bertrand Russell (1910-12),
Principia mathematica, 3 Vol., Cambridge University
Press
Il concetto di grandezza
Tentiamo di rendere meno criptica questa definizione, partendo
dalla nozione di relazione di equivalenza
In matematica il concetto di relazione di equivalenza esprime
l’idea di similitudine tra oggetti. Formalmente, la relazione di
equivalenza è una relazione binaria (cioè una corrispondenza tra
due oggetti che indicheremo come ~ e leggeremo come
“equivalente a”)
Dato un insieme A, una relazione binaria ~ è una relazione di
equivalenza se è riflessiva (per ogni elemento a appartenente
all’insieme A, deve risultare che a~a); simmetrica (per ogni
coppia a, b di elementi di A, a~b implica b~a); transitiva (per ogni
terna (a, b, c ) di elementi di A, se a~b e b~c allora a~c)
Il concetto di grandezza
Due elementi tra i quali sussiste una relazione di equivalenza ~ si
dicono equivalenti, in quanto la proprietà di simmetria ci
consente di prescindere dall’ordine con cui quegli elementi
compaiono all’interno della relazione
Un sottoinsieme di A che contiene tutti e solo gli elementi
equivalenti a un qualche elemento a di A prende il nome di classe
di equivalenza di a, in simboli [a]~ o anche {a}~
Definiremo insieme quoziente per la relazione di equivalenza ~
l'insieme delle classi di equivalenza su A e indicheremo questa
particolare partizione su A con l'espressione A/~.
Il concetto di grandezza
Esempio
Un esempio di insieme quoziente è costituito dai numeri
razionali. I numeri razionali possono essere costruiti come
l’insieme delle classi di equivalenza di coppie di numeri interi (a,
b), con b diverso da zero, dove la relazione di equivalenza è
definita come (a, b) ~ (c, d) se e solo se ad = bc
In questo caso, la classe di equivalenza a cui appartiene (a, b) è
identificata con la frazione a/b.
Il concetto di grandezza
Con queste nozioni, siamo in grado di definire formalmente il
concetto di grandezza
Definiamo grandezza una classe di equivalenza di proprietà
misurabili. Condizione necessaria affinché una classe di
equivalenza di proprietà sia misurabile è che sia possibile stabilire
una relazione d’ordine fra quelle proprietà in sistemi diversi:
poter giudicare quale sistema presenta «più» proprietà dell’altro
Se il confronto si svolge tramite un rapporto fra le proprietà dei
due sistemi, allora la classe di equivalenza di quelle proprietà è
una grandezza
Il concetto di grandezza
In questo caso, è possibile scegliere la proprietà di un particolare
sistema ed eleggerla a unità di misura per quella grandezza
Fissata l’unità di misura, la quantità di tale grandezza per un
qualsiasi altro sistema potrà essere univocamente specificata da
un valore numerico ottenuto dal rapporto con la proprietà scelta
come campione di riferimento
Il concetto di grandezza
Esempio
Pensiamo al concetto di lunghezza. La lunghezza è una proprietà
astratta dello spazio. Il chilometro è un termine astratto che
partecipa del concetto di lunghezza; così pure il metro, il
centimetro, il micron, sono tutti termini compresi nel concetto di
lunghezza e quindi partecipano di quel concetto
I termini «chilometro», «metro», «centimetro», «micron» stanno
fra loro nel rapporto di maggiore o minore: infatti un chilometro
è maggiore di un metro, un centimetro è maggiore di un micron
ed è minore di un metro
Quindi chilometro, metro, centimetro, micron sono grandezze,
mentre la lunghezza è una classe di grandezze, riferita ad una
proprietà astratta dello spazio
Il concetto di grandezza
Torniamo adesso a quanto detto all’inizio della presente sezione
e domandiamoci qual è lo scopo del confronto fra grandezze
In generale, confrontiamo grandezze per cogliere le diversità
esistenti tra gli stati attraverso i quali un fenomeno si manifesta,
operazione indispensabile ai fini della conoscenza del mondo
reale
Il confronto fra grandezze è cruciale, anche quando non riguarda
grandezze omogenee o, comunque, direttamente confrontabili:
garantire coerenza e significatività ai risultati di un confronto,
quindi, implica affrontare e risolvere problemi complessi
Le scale di misura
Misurazione
Assegnazione di valori numerici ad eventi/oggetti, secondo regole
definite, che permette di rappresentare le proprietà di un
evento/oggetto con le proprietà del sistema numerico
Le regole tramite le quali i valori numerici sono assegnati agli eventi
determinano le caratteristiche della misura
Le scale di misura
Variabile: è la proprietà operativizzata, cioè rilevata sui casi attraverso
una procedura di «definizione operativa». Nel caso di caratteri
qualitativi (non definiti su spazi numerici) si parlerà di mutabile
Le variabili si classificano in
1.
2.
3.
4.
Qualitative (variano in genere) e quantitative (variano in grandezza)
Nominali, ordinali e cardinali
Dicotomiche e politomiche
Continue/discrete
Le scale di misura
Scala nominale
1. Permette di classificare eventi e oggetti in categorie
2. I differenti stati assunti dal fenomeno sono indicati da una qualità
non numerica (es. colore, genere). Gli stati stessi non possono
essere ordinati con un criterio del tipo maggiore/minore
3. Operazioni ammesse: uguale/diverso
4. Indicatori di sintesi: moda
Le scale di misura
Esempio di fenomeno definito su scala nominale
Ipotizziamo di domandare a 8 ragazzi di quale colore sceglieranno il
prossimo smartphone e di raccogliere le loro risposte nel seguente
prospetto:
Unità di rilevazione
Marco
Giorgio
Rebecca
Claudia
Alessia
Matteo
Vanessa
Nicholas
Colore
preferito
Nero
Bianco
Arancione
Bianco
Nero
Verde
Bianco
Bianco
Le scale di misura
Esempio di fenomeno definito su scala nominale
Possiamo sintetizzare le loro risposte in una tabella costruita nel modo
seguente:
Colore preferito
(X)
Nero
Bianco
Arancione
Verde
Totale
Frequenza
assoluta
( Nx )
2
4
1
1
Frequenza
relativa
( fx )
0,250
0,500
0,125
0,125
8
1,000
Le scale di misura
Scala ordinale
1. Dispone oggetti ed eventi in sequenza in base a un ordine
convenzionale (es. gradi militari)
2. Dà solo l’ordine degli oggetti/eventi
3. Operazioni ammesse:
– uguale/diverso
– maggiore/minore
4. Indicatori di sintesi: moda, mediana
Le scale di misura
Esempio di fenomeno definito su scala ordinale
Ipotizziamo di aver rilevato il livello di scolarità all’interno di un
collettivo di N = 100 dipendenti di una società multinazionale e di aver
sintetizzato i risultati della rilevazione nel seguente prospetto:
Livello di scolarità
(X)
Nessun titolo
Licenza elementare
Scuola media inferiore
Scuola media superiore
Laurea triennale
Laurea specialistica
Master/Dottorato
Totale
Frequenza
assoluta
( Nx )
0
1
4
40
35
15
5
Frequenza
relativa
( fx )
0,00
0,01
0,04
0,40
0,35
0,15
0,05
100
1,00
Frequenza
relativa
cumulata
( cx )
0,00
0,01
0,05
0,45
0,80
0,95
1,00
Le scale di misura
Scala intervallare
1. Lo zero della scala (l’origine del sistema di riferimento) è arbitrario
(es.: scala Celsius, scala Fahrenheit)
2. I confronti possono essere svolti solo tramite differenze
3. Operazioni ammesse:
– uguale/diverso
– maggiore/minore
– somma, sottrazione
4. Indicatori di sintesi: moda, mediana, media aritmetica, altri
parametri di forma
Esempio: 𝐹 = 32 + 1,8 ∙ 𝐶
Sistema di riferimento Celsius: Roma 10C° Milano 5C°
Sistema di riferimento Fahrenheit: Roma 50F° Milano 41F°
Le scale di misura
Esempio di fenomeno definito su scala intervallare
Ipotizziamo di aver registrato la temperatura alle ore 12 del 3 e del 4
marzo in alcuni capoluoghi italiani. Le informazioni potrebbero essere
organizzate nel seguente prospetto:
Unità di rilevazione
Roma
Milano
Torino
Bologna
Napoli
Bari
Palermo
Temperatura
rilevata alle 12
del 03/03/2015
( C° )
16
12
11
13
15
17
20
Temperatura
rilevata alle 12
del 04/03/2015
( C° )
17
14
12
14
16
18
21
Le scale di misura
Esempio di fenomeno definito su scala intervallare
Il relativo prospetto di sintesi potrebbe essere strutturato nel modo
seguente:
Temperatura
(X)
[10, 14)
[14, 18)
[18, 22]
Totale
Frequenza
assoluta
03/03/2015
( Nx )
3
3
1
Frequenza
assoluta
04/03/2015
( Nx )
1
4
2
Frequenza
relativa
03/03/2015
( fx )
0,429
0,429
0,143
Frequenza
relativa
04/03/2015
( fx )
0,143
0,571
0,286
7
7
1,000
1,000
Le scale di misura
Scala proporzionale (o di rapporti)
1. Lo zero della scala è reale (corrisponde all’assenza della variabile)
2. I rapporti fra i valori numerici hanno significato
3. Operazioni ammesse:
– uguale/diverso
– maggiore/minore
– addizione, sottrazione, moltiplicazione, divisione
4. Indicatori di sintesi: moda, mediana, medie di potenze, altri
parametri di forma, altri rapporti statistici
Le scale di misura
Esempio di fenomeno definito su scala proporzionale
Ipotizziamo di rilevare la retribuzione netta mensile all’interno del
collettivo di N = 100 dipendenti di una società multinazionale e di aver
sintetizzato i risultati della rilevazione nel seguente prospetto:
Retribuzione
netta mensile
(X)
[500, 1000)
[1000, 1500)
[1500, 2000)
[2000, 2500)
[2500, 3000]
Totale
Frequenza
assoluta
( Nx )
8
30
42
15
5
Frequenza
relativa
( fx )
0,08
0,30
0,42
0,15
0,05
100
1,00
Frequenza
relativa
cumulata
( cx )
0,08
0,38
0,80
0,95
1,00
Materiali per la preparazione dell’esame
•
•
•
Giuseppe Leti, Loredana Cerbara (2009), Elementi di statistica descrittiva, Il
Mulino, Bologna
Slides
Altro materiale (testi di esercitazioni, esercizi svolti, complementi) diffuso su
Moodle e sul gruppo di discussione di Facebook
Per ogni ulteriore chiarimento o esigenza informativa:
[email protected]