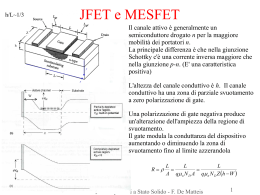
Capacità MOS
Strato di ossido su di un semiconduttore drogato p
Un contatto metallico è deposto sull'ossido
Lo strato di ossido isola il metallo
dal semiconduttore → No corrente
Caso ideale:
•A zero bias
qV fb  q m  s   0
(Condizione di bande piatte)
•Non ci sono stati di interfaccia tra
semiconduttore e isolante
•I livelli di energia sono disposti così da
eliminare ogni gradiente di potenziale
•Alta barriera tra metallo e semiconduttore
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
1
Capacità MOS
La piegatura delle bande è
determinata dalla differenza di
funzione lavoro tra metallo e
semiconduttore.
=0
Può essere positiva o negativa in
funzione della scelta del metallo e
del semiconduttore (e del
drogaggio di quest'ultimo)
Nel caso illustrato il metallo è a un
potenziale Vfb negativo rispetto al
semiconduttore.
Applicando un potenziale esterno
(positivo) si ripristina la condizione
di bande piatte
Campo di polarizzazione dielettrica
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
2
Capacità
MOS
Tre diversi regimi di funzionamento
Accumulazione di buche: applicando un bias negativo
(NB piegamento delle bande maggiore di quello a Vfb).
Cariche negative accumulate sul lato metallo e cariche
positive sul lato semiconduttore
Fino a 0<VGS=-Vfb
Condizione di bande piatte
Svuotamento: applicando un bias più positivo si
inverte la piegatura delle bande (VGS>-Vfb ).
Accumulo di carica negativa sul lato semiconduttore
(si accumulano nei livelli accettori – cariche fisse)
Inversione: applicando un bias ancora più positivo la
densità di carica negativa all'interfaccia sul lato
semiconduttore aumenta fortemente.
(livelli accettori saturi + cariche libere) Localmente (nel canale conduttivo) diventa tipo-n
La tensione massima di inversione dipende dall'isolante e la sua interfaccia (assenza di difetti di
interfaccia)
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
3
Capacità MOS
Mettiamo in relazione la piegatura delle bande eVs con la differenza tra l'energia di
Fermi intrinseca e l'energia di Fermi di bulk EFi -EF = e
Quando Vs è nullo le bande sono piatte.
Fissiamo come criterio per l'inversione che Vs(inv)=-2F ovvero che la concentrazione
di portatori n all'interfaccia sia pari alla concentrazione di portatori p di bulk (per un
semiconduttore p)
k T
p
F  B ln
e
ni
E' un criterio arbitrario ma il senso è
che all'inversione si hanno all'incirca
1011cm-2 elettroni nel canale
conduttivo sotto il Gate.
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
4
Soglia MOS
La carica accumulata sul metallo Qm (positiva) è bilanciata dalla carica sul semiconduttore costituita
dalle cariche di svuotamento Qd (per la piegatura delle bande buche si allontanano dalla superficie
lasciando i livelli accettori carichi negativamente) e dalle cariche libere create in banda di conduzione Qn
Qs   s Fs
Legge di Gauss sulla interfaccia
La tensione di Gate può essere scritta
 s Fs   ox Fox
Continuità di D
VGS = Vfb + Vox + Vs
 s Fs
 s Fs Qs
Vox  Fox d ox 
d ox 

 ox
Cox Cox
Capacità per unità d'area dell’ossido
Alla tensione di soglia VT alla quale inizia l'inversione
la carica è solo quella di svuotamento Qs=eNaW
W
2 s Vs
eN a
Qs  2 s eN a Vs
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
5
Polarizzazione MOS
Se il substrato è polarizzato ad una tensione Vsub, anche la tensione di gate per la soglia
aumenterà
VGS  VT  Vsub
Se c’è una tensione tra sorce e substrato VSB il potenziale di superficie necessario a produrre
inversione diverrà -2F+VSB
VT  V fb  2F

2e N

s
a  2 F  VSB 
1/ 2
Cox
Se nell’ossido sono presenti impurezze con densità di carica Nt(z) ci sarà una caduta di
potenziale aggiuntiva
VT 
e
Cox

dox
0
zN t ( z )
dz
d ox
L’effetto delle cariche di carica di interfaccia è max all’interfaccia ossido-semiconduttore
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
6
Caratteristica Tensione-Capacità
La capacità del Gate è costituita dalla serie della capacità dell'ossido e di quella del
semiconduttore
dQ
Cs 
In regime di accumulazione (tensione di gate
negativa) le buche si accumulano sulla
superficie e la capacità Cs diventa molto
larga: piccole variazioni di tensione
generano grandi variazioni di carica Cmos  Cox
Per tensioni di gate positive ancora più marcate
cominciano ad accumularsi cariche libere e la
regione di svuotamento non si accresce più. la
capacità Cs torna a crescere
Cmos  Cox
Cox 
s
dVs
d ox
Per tensioni di gate positive
il canale si svuota di buche,
1
Cmos 
la capacità Cd diventa
1
 1
Cox
Cs
importante

Cs  Cd  s
W
 ox
Cmos 

d ox  ox W
s
Abbiamo assunto che le cariche
libere nel regime di inversione
sono fornite istantaneamente ma
questo non è il caso. Queste in
realtà vengono da generazione di
coppie e diffusione di portatori
minoritari. Contributo presente
solo a bassa frequenza.
LM Fisica A.A.2013/14
 ox
Fisica dei Dispositivi a Stato Solido - F. De Matteis
7
Effetto delle impurezze
La presenza di cariche fisse porta ad una
caduta di potenziale sull’ossido
 Qss
V 
Cox
Per cariche positive si ha lo spostamento della
curva verso valori più negativi
Indipendente dalla polarizzazione quindi shift
rigido.
Stati di impurezze all’interfaccia generano stati
accessibili a elettroni nel semiconduttore con
occupazione dipendente dal livello di Fermi e quindi
dalla tensione applicata.
L’effetto è di spianare la curva
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
8
Transistor MOSFET
Abbiamo visto come si comporta il condensatore MOS sul gate. La creazione di
cariche libere apre un canale conduttivo tra source e drain. Il MOSFET è un
dispositivo estremamente importante.
Le assunzioni fatte in precedente sono applicate anche in questo caso
- La mobilità degli elettroni è costante e indipendente dal campo
- Il canale conduttivo ha uno sviluppo bidimensionale. Approssimazione di canale
graduale. Il campo nella direzione gate-substrato è molto più forte che nella direzione
source-drain. Il potenziale lungo il canale varia lentamente
VGS
Qs
 VT 
 Vc (x)
Cox
Vc(x) Tensione oltre la soglia di inversione
lungo il canale conduttivo
dVc ( x)
I D  AtrasvF  Qs  n
Z
dx
Strizzamento per VDS(sat)
L
L
0
0
 I D dx  I D L   Qs n Z dVc ( x)
VDS 

  n ZCox VGS  VT 
VDS

2 

LM Fisica A.A.2013/14
VDS Qs ( x  L)  0  VGS  VT
Oltre la situazione di pinch-off
la corrente rimane costante
Fisica dei Dispositivi a Stato Solido - F. De Matteis
9
Caratteristiche I-V
Qs sat 
 VGS  VT  VDS sat 
Cox
pinch-off
VDS sat   VGS  VT
Regione lineare o Ohmica
VDS<VDS(sat)=VGS-VT
Regione di saturazione VDS>VDS(sat)=VGS-VT
ID 
 n ZCox 
L
 n ZCox 
VGS  VT VDS

  V
L
VGS  VT

 n ZCox
VGS  VT 2
2L
2
LM Fisica A.A.2013/14
GS
2

VDS


2 
 VT
2
  
2

Fisica dei Dispositivi a Stato Solido - F. De Matteis
10
ID 
Caratteristiche I-V
n ZCox 
2

VDS


V

V
V

 GS T DS

2 

L
Regione lineare o Ohmica
ID 
 n ZCox
L
VGS  VT VDS 
La mobilità nel canale MOSFET è ridotta a
causa dello scattering all'interfaccia Si-SiO2
gD 
I D
VDS

VGS const
 n ZCox
L
VGS  VT 
Conduttanza di drain (va minimizzata)
Regione di saturazione
ID 
Transconduttanza
Max per piccole L e grandi 
LM Fisica A.A.2013/14
 n ZCox
2L
gm 
VGS  VT 2
I D
VGS

VDS const
 n ZCox
L
VGS  VT 
Fisica dei Dispositivi a Stato Solido - F. De Matteis
11
Effetti della tensione di substrato
La tensione source-Substrato VSB è una
variabile addizionale. Se questa è zero o
positiva la giunzione source-substrato è
polarizzata inversa.
Per VSB=0 la condizione di inversione
avviene per Vs = -2F Se VSB>0 la tensione
di superficie è aumentata di una quantità
VSB
Lo spessore di svuotamento aumenta per
assorbire l'aumento di potenziale
La variazione di tensione di soglia è
2e s N a
VT 
Cox

 2F  VSB  2F

Fisica dei Dispositivi a Stato Solido - F. De Matteis
12
Configurazioni MOS
Aumentando la tensione di gate fino ad una tensione
positiva VT arriviamo all'inversione e il dispositivo
inizia a condurre, si accende.
E' la configurazione illustrata finora.
Configurazione in modo di incremento
Ma c'è una configurazione alternativa in cui il
dispositivo è acceso in assenza di polarizzazione di
gate. E che si spegne quando è applicata una tensione
di gate.
Configurazione in modo di svuotamento
Su di un substrato di tipo p si crea un sottile canale di
tipo n facendo diffondere uno strato di donori tra i due
contatti (source e drain) n+ Dopodiché si crea lo strato
di ossido e il gate.
Il dispositivo ha normalmente un canale conduttivo
finché non imponiamo una tensione che inverte la
popolazione dei portatori.
Fisica dei Dispositivi a Stato Solido - F. De Matteis
13
Complementary MOSFET
CMOS
Un dispositivo in modo di svuotamento è acceso se il gate non è
polarizzato e il gate può essere usato per spegnere il dispositivo.
Come ogni FET il dispositivo sarà conduttivo in uno degli stati. Questo
causa dissipazione di potenza nel circuito. In un circuito integrato ciò
può causare problemi seri.
Per evitare ciò si combina un dispositivo a n-canale in serie a un p-canale
sullo stesso chip.
Il drain del n- e del p-MOSFET sono connessi e
formano l'uscita. L'ingresso è portato ad entrambi i
gate. Il dispositivo PMOS ha soglia negativa mentre il
NMOS ha tensione di soglia positiva.
Quando una tensione di ingresso nulla è applicata
all'ingresso la tensione tra sorgente e gate del
dispositivo NMOS è zero ed il MOSFET è spento.
Invece la tensione tra gate e source del PMOS è -V
perché il source è a +V; e il PMOS è acceso. La
tensione di uscita è quindi V. E viceversa.
NON SCORRE CORRENTE ATTRAVERSO IL
CANALE SOURCE-DRAIN-SOURCE
Fisica dei Dispositivi a Stato Solido - F. De Matteis
14
Long channel MOSFET
Processo di inversione puntuale. No-conduzione fino a
soglia poi conduzione completa.
In realtà i portatori nel canale cambiano gradualmente con
la tensione di gate.
Corrente aumenta gradualmente e anche se spento il
dispositivo consuma potenza nello stato OFF.
Conduzione sotto soglia
Meccanismo dominante è diffusione
n(0)  ni e q  s  F / kT
n( L)  ni e q  s  F VD / kT
 s  VG  VT
Fisica dei Dispositivi a Stato Solido - F. De Matteis
15
Long channel MOSFET
Variazioni della mobilità con il gate bias
Abbiamo assunto che la mobilità non varia con la tensione di gate. La densità di
elettroni varia con la tensione di gate ed è legata al campo sulla superficie Fs:
aumentando la carica di superficie aumenta il campo di superficie e gli elettroni sono
forzati in prossimità dell'interfaccia dove subiscono maggior scattering e la mobilità
degrada.
Variazioni della mobilità
con il campo
La mobilità non è
indipendente dal campo
applicato. Ad ad alto
campo sovrastimiamo la
mobilità.
μn F
v F  =
μn F
vs
Fattore di riduzione
1+
Fisica dei Dispositivi a Stato Solido - F. De Matteis
16
Long channel MOSFET
Modulazione della lunghezza del canale
in regione di saturazione
Quando VDS>VD(sat) il canale si strizza
all'estremo del drain e la corrente rimane
costante. Ma il canale si accorcia e quindi
la corrente aumenta


L

I D = I D sat 
 L  ΔL VDS  
Effetti di radiazione e breakdown
Radiazioni ionizzanti (applicazioni spaziali) generano cariche fisse e di interfaccia.
La tensione di soglia si sposta. Perdita di funzione di circuito e inusuale dissipazione.
Il brakdown avviene per rottura dell'isolante che può essere molto sottile.
Fisica dei Dispositivi a Stato Solido - F. De Matteis
17
MOSFET come carico
Resistenze anche alte su piccole (o piccolissime) aree.
MOSFET in modo aumentato Drain e gate sono accoppiati. Resistenza nonlineare
(Dispositivo sempre in saturazione)
MOSFET in svuotamento Source e gate accoppiati VGS=0
Fisica dei Dispositivi a Stato Solido - F. De Matteis
18
MOSFET come inverter
Si costruisce uno switch accoppiando ad un opportuno carico resistivo RL (può essere anche
un altro MOSFET)
MOSFET in svuotamento. Linea di carico è una retta con intercetta VDS(ID=0)=VDD e
ID(VDS=0)=VDD/RL
RL I D  VDS = VDD
Fisica dei Dispositivi a Stato Solido - F. De Matteis
19
CCD Charge Coupled Device
Immagazinamento di carica e azione di trasferimento controllato dal Gate. Tutti gli elettrodi sono
polarizzati positivamente per produrre uno svuotamento di superficie. L’elettrodo centrale è svuotato di
più. Buca di potenziale
Cariche minoritarie (elettroni) sono introdotti e poi passo passo trasferite a destra
1
2
2
3
1
2
3
4
3
Fisica dei Dispositivi a Stato Solido - F. De Matteis
20