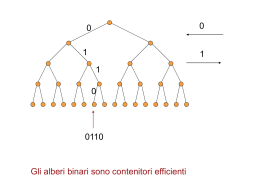
prototipo di crescita esponenziale
crescita aritmetica
da notare
ricorsione
?
?
+
=
dimostrazione alternativa
?
come dimostrarlo ?
induzione
vero per n=0
se vero per (n-1) allora vero per n
Teorema: Tutti i gatti hanno lo stesso colore:
Dimostrazione:
base dell induzione: un gatto ha lo stesso colore (ovvio)
passo induttivo:
ogni insieme di n-1 gatti ha lo stesso colore.
Dato un insieme di n gatti, si prendano i gatti da 1 a n-1.
Devono avere lo stesso colore.
Si prendano i gatti da 2 a n. Devono avere lo stesso colore.
Ma i gatti da 2 a n-1 hanno anche lo stesso colore.
Quindi tutti gli n gatti hanno lo stesso colore.
Dove sta l’errore ?
Chi cresce di più ?
Ma per n=997 avviene il sorpasso
Racconto del poeta arabo al-Sabhadi (Bagdad 1000 d.C)
sull’origine degli scacchi
Motivazione: facilità del calcolo di 2 alla 64
con il metodo indiano
01101001101001111001
Quante stringhe di 0 e 1 di lunghezza n ?
Insieme
Quanti sottoinsiemi ?
Quanti sottoinsiemi di m elementi ?
n volte
Scelta di non prendere
l’elemento
Scelta di prendere l’elemento
Il coefficiente di
e` il numero di insiemi di m elementi
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1
2
4
8
16
1 5 10 10 5 1
32
1 6 15 20 15 6 1
64
0
0
1
1
1
0
0110
Gli alberi binari sono contenitori efficienti
MARIO
SANDRA
ELISA
VALERIO
BRUNO
FABIO
CARLO
ANDREA
FILIPPO
EMILIA
ALBERTO
ANNA
PAOLO
DANIELA
FRANCO
MINO
ROBERTO
NICOLA
MICHELE
ALBERO BINARIO DI RICERCA
STEFANO
UGO
ELENA
MARIO
SANDRA
ELISA
VALERIO
BRUNO
FABIO
CARLO
ANDREA
FILIPPO
EMILIA
ALBERTO
ANNA
PAOLO
DANIELA
FRANCO
MINO
ROBERTO
NICOLA
MICHELE
ALBERO BINARIO DI RICERCA
STEFANO
UGO
MARIO
ELENA
SANDRA
ELISA
VALERIO
BRUNO
FABIO
CARLO
ANDREA
FILIPPO
EMILIA
ALBERTO
ANNA
PAOLO
DANIELA
FRANCO
MINO
ROBERTO
NICOLA
MICHELE
ALBERO BINARIO DI RICERCA
STEFANO
UGO
MARIO
SANDRA
ELISA
ELENA
VALERIO
BRUNO
FABIO
CARLO
ANDREA
FILIPPO
EMILIA
ALBERTO
ANNA
PAOLO
DANIELA
FRANCO
MINO
ROBERTO
NICOLA
MICHELE
ALBERO BINARIO DI RICERCA
STEFANO
UGO
MARIO
SANDRA
ELISA
VALERIO
BRUNO
FABIO
PAOLO
ELENA
CARLO
ANDREA
FILIPPO
EMILIA
ALBERTO
ANNA
DANIELA
FRANCO
MINO
ROBERTO
NICOLA
MICHELE
ALBERO BINARIO DI RICERCA
STEFANO
UGO
MARIO
SANDRA
ELISA
VALERIO
BRUNO
FABIO
CARLO
ANDREA
PAOLO
FILIPPO
EMILIA
MINO
ROBERTO
STEFANO
ELENA
ALBERTO
ANNA
DANIELA
FRANCO
NICOLA
MICHELE
ALBERO BINARIO DI RICERCA
UGO
MARIO
SANDRA
ELISA
VALERIO
BRUNO
FABIO
CARLO
ANDREA
FILIPPO
EMILIA
DANIELA
ALBERTO
PAOLO
ANNA
FRANCO
MINO
ROBERTO
NICOLA
MICHELE
ELENA
ALBERO BINARIO DI RICERCA
STEFANO
UGO
F
R
F
E
E
E
H
T
M
H
M
B
C
B
N
Z
P
B
B
B
P
Dati n giocatori, come costruire il tabellone ?
Dati n giocatori, quante sono le partite ?
Disponendo di molti campi, quanto dura il torneo ?
Disponendo di m campi, quanto dura il torneo ?
Dati n giocatori, quante sono le partite ?
trovare un invariante
per ogni partita c’è una vittoria e una sconfitta
ogni giocatore (tranne il vincitore del torneo) perde esattamente una volta
il numero di partite è uno meno del numero di giocatori
e le vittorie come sono distribuite ?
esiste una qualche regolarità o no?
il vincitore vince sempre
c’è qualcuno che non vince mai (cioè gioca una sola volta e perde)?
vittorie
partite =
esattamente uno?
almeno uno che non vince esiste
A
B
B
C
C
D
D
E
E
e le vittorie come sono distribuite ?
esiste una qualche regolarità o no?
il vincitore vince sempre
c’è qualcuno che non vince mai (cioè gioca una sola volta e perde)?
vittorie
partite =
nessuno vince (tranne uno)
A
A
B
A
C
A
D
A
E
Disponendo di molti campi, quanto dura il torneo ?
7+11+5+13+6+8+4+10+9+15+12+6+8+16
7
11
5
13
6
8
4
10
9
15
12
6
18
36
18
64
14
28
14
130
24
42
18
66
8
24
16
tempo logaritmico
con sufficienti processori
35
19
22
7
17
21
10
9
15
3
6
6 1 8 1 7 9 2 2 5 6 3
8
12
19
22
7
17
21
10
9
15
3
6
6 1 8 1 7 9 2 2 5 6 3
Rimozione del massimo
8
12 7
4
3
19
22
7
17
21
10
9
15
3
6
6 1 8 1 7 9 2 2 5 6
Rimozione del massimo
8
12 7
4
22
19
3
7
17
21
10
9
15
3
6
6 1 8 1 7 9 2 2 5 6
Rimozione del massimo
8
12 7
4
22
19
21
7
17
3
10
9
15
3
6
6 1 8 1 7 9 2 2 5 6
Rimozione del massimo
8
12 7
4
22
19
21
10
7
17
15
9
3
3
6
6 1 8 1 7 9 2 2 5 6
Rimozione del massimo
8
12 7
4
22
19
21
10
7
17
15
9
9
3
6
8
12 7
4
6 1 8 1 7 3 2 2 5 6
Rimozione del massimo
costo log n
35
19
22
7
17
21
10
9
15
3
6
8
12 7
6 1 8 1 7 9 2 2 5 6 3 18
Aggiungere un elemento
4
35
19
22
7
17
21
10
9
15
3
6
8
18 7
6 1 8 1 7 9 2 2 5 6 3 12
Aggiungere un elemento
4
35
19
22
7
18
21
10
9
15
3
6
8
17 7
4
6 1 8 1 7 9 2 2 5 6 3 12
Aggiungere un elemento
costo log n
22
19
21
10
7
17
15
9
9
3
6
6 1 8 1 7 3 2 2 5 6
35
8
12 7
4
19
21
10
7
17
15
9
9
3
6
6 1 8 1 7 3 2 2 5 6
35
22
8
12 7
4
6
19
21
10
7
17
15
9
9
3
6
6 1 8 1 7 3 2 2 5
35
22
8
12 7
4
21
19
6
10
7
17
15
9
9
3
6
6 1 8 1 7 3 2 2 5
35
22
8
12 7
4
21
19
15
7
17
6
10
9
9
3
6
6 1 8 1 7 3 2 2 5
35
22
8
12 7
4
21
19
15
9
10
7
9
6
17
3
6
6 1 8 1 7 3 2 2 5
35
22
8
12 7
4
21
19
15
9
10
7
9
7
17
3
6
6 1 8 1 6 3 2 2 5
35
22
8
12 7
4
5
19
15
9
10
7
9
7
17
3
6 1 8 1 6 3 2 2
35
22
21
6
8
12 7
4
19
15
5
9
10
7
9
7
17
3
6 1 8 1 6 3 2 2
35
22
21
6
8
12 7
4
19
15
17
10
7
5
9
9
7
3
6 1 8 1 6 3 2 2
35
22
21
6
8
12 7
4
19
15
17
9
10
7
9
7
12
3
6 1 8 1 6 3 2 2
35
22
21
6
8
5
7
4
alberi genealogici
padre
nonno
madre
nonna
nonno
nonna
piccolo conto
3 generazioni per secolo
30 generazioni fino all’anno 1000
un miliardo !
non esistevano tanti abitanti
?
1) molti antenati sono la stessa persona
2) abbiamo tutti antenati comuni
A
B
C
D
E
G
H
I
J
K
M
N
F
Codice Morse (apparentemente) binario
A
B
C
D
E
F
G
H
I
J
K
L
M
01
1000
1010
100
0
0010
110
0000
00
0111
101
0100
11
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
10
111
0110
1101
010
000
1
001
0001
011
1001
1011
1100
Codice Morse (apparentemente) binario
A
B
C
D
E
F
G
H
I
J
K
L
M
01
1000
1010
100
0
0010
110
0000
00
0111
101
0100
11
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
10
111
0110
1101
010
000
1
001
0001
011
1001
1011
1100
Codice Morse (apparentemente) binario
A
B
C
D
E
F
G
H
I
J
K
L
M
01
1000
1010
100
0
0010
110
0000
00
0111
101
0100
11
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
10
111
0110
1101
010
000
1
001
0001
011
1001
1011
1100
Codice Morse (apparentemente) binario
A
B
C
D
E
F
G
H
I
J
K
L
M
01
1000
1010
100
0
0010
110
0000
00
0111
101
0100
11
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
10
111
0110
1101
010
000
1
001
0001
011
1001
1011
1100
Codice Morse (apparentemente) binario
A
B
C
D
E
F
G
H
I
J
K
L
M
01
1000
1010
100
0
0010
110
0000
00
0111
101
0100
11
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
10
111
0110
1101
010
000
1
001
0001
011
1001
1011
1100
arrivo domani
01010010000001111 10011111011000
0101001000000111110011111011000
entelesomitongi
00
011
0100
0101
100
110
1010 1011
010100100000011111001111101100
111
Codice di Huffman
a
e
m
p
r
t
z
16
25
12
6
10
8
2
Codice di Huffman
a
e
m
p
r
t
z
16
25
12
6
10
8
2
minimi
z
p
Codice di Huffman
a
e
m
(pz)
r
t
16
25
12
8
10
8
minimi
t
z
p
Codice di Huffman
a
e
m
(pzt)
r
16
25
12
16
10
minimi
t
z
p
m
r
Codice di Huffman
a
e
(mr)
(pzt)
16
25
22
16
minimi
a
t
z
p
m
r
Codice di Huffman
(apzt)
e
(mr)
32
25
22
minimi
a
e
t
z
p
m
r
Codice di Huffman
(apzt)
(emr)
a
e
m
p
r
t
z
32
47
a
16
25
12
6
10
8
2
e
t
z
p
m
r
00
11
100
0101
101
011
0100
alberi binari come contenitori di tutti i razionali
albero di Stern-Brocot
Ogni frazione è rappresentata da numeri primi fra loro
Ogni razionale è presente
Nessun razionale è ripetuto
Nessun razionale è ripetuto
s
r
r
3 2 - 1 5 =1
5 2 - 3 3 =1
Ogni razionale e` presente
0
1
0
010
1
1
0
0
010
1100
101100
ogni razionale è associato ad una stringa di 0 e 1
e gli irrazionali ?
ogni irrazionale è associato ad una stringa infinita di 0 e 1
100110011001100110011….
1 2 2 2 2 2 2 2 2 2 2
1 0 1 0 1 0 1 0 1 0 1….
1 2 2 2 2 2 2 2 2 2 2 ….
e
11011010000101111110100000000….
2 1 2 1 1 4 1 1 6 1 1 8
1 0 1 0 1 0 1 0 1 0 1 0….
2 1 2 1 1 4 1 1 6 1 1 8 ….
1010101010101010...
1 1 1 1 1 1 1 1 1 1 1 1 ….
nella musica
frequenza del la(1)
110 Hz
1
frequenza del la(2)
220 Hz
2
frequenza del la(3)
440 Hz
4
frequenza del la(4)
880 Hz
8
frequenza del la(5)
1760 Hz
16
frequenza del la(6)
3520 Hz
32
e le note intermedie ?
e le note intermedie ?
e le note intermedie ?
sol
fa
mi
la
sol
fa
la
mi
re
si
2
4
8
16
32
64
La torre di Hanoi
Regole:
1) Spostare i dischi uno alla volta
2) Ogni disco deve sempre poggiare su uno più grande
Domanda:
Quanti spostamenti sono necessari per trasferire
tutti i dischi da un piolo ad un altro ?
1
1
1