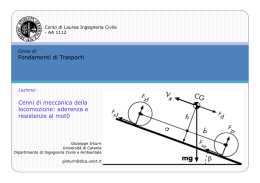
Corso di Sistemi di Trazione Lezione 3: Resistenze al moto dei veicoli, richiami dei principi della dinamica applicati ai veicoli A. Alessandrini – F. Cignini – C. Holguin – D. Stam AA 2014-2015 Obiettivi • • • • Definire quali forze influenzano il moto dei veicoli Comprendere i principi fisici che governano queste forze Analizzare l’espressione analitica che le caratterizza Fornire un modello dinamico di veicolo da poter usare nei modelli Argomenti • • • In quali condizioni si possono calcolare le massime prestazioni Cos’è un veicolo e come si schematizza La resistenze al moto e in particolare: – – – – • Al rotolamento degli pneumatici Aerodinamica Superamento della pendenza Inerzia Come si calcola la massa ‘‘corretta’’ Cosa influenza il moto dei veicoli? • • • • • Le caratteristiche del veicolo stesso Le capacità ed il comportamento del guidatore Le caratteristiche della strada Le condizioni atmosferiche L’interazione con gli altri veicoli 1a Fase: Determinare le massime prestazioni di un’auto • Considerando assenti altri veicoli; • definendo la strada: – piatta, rettilinea e indefinitamente lunga; • fissando le condizioni atmosferiche; • scegliendo un guidatore che ha come unico obiettivo di andare sempre alla massima velocità • il comportamento del veicolo dipende esclusivamente dalle sue caratteristiche. Un utile ricordo • I principi della dinamica: 1 3 2 • Un corpo mantiene il suo stato di quiete o moto rettilineo e uniforme finché non intervenga una forza esterna a turbarlo Un sistema di forze agenti su un corpo è sempre equilibrato Quando un corpo è soggetto ad un sistema non equilibrato di forze il sistema viene equilibrato dalla forza di inerzia (derivata dalla quantità di moto) Determinazione delle reazioni vincolari in un semplice sistema isostatico Festerna R 1vert R 1or R 2vert Che cos’è un veicolo per il corso • Le caratteristiche costruttive del veicolo e del suo sistema di trazione • Le resistenze che incontra e le forze che influiscono sul suo moto Le resistenze e le forze che influiscono sul moto del veicolo • La resistenza al rotolamento dei pneumatici • La resistenza aerodinamica • La forza necessaria al superamento della pendenza • La forza d’inerzia La resistenza al rotolamento • Perché un pneumatico rotolando oppone resistenza? In recesso i vettori velocità e posizione sono discordi Isteresi elastica In accesso i vettori velocità e posizione sono concordi L’influenza dell’isteresi elastica sulla distribuzione delle pressioni Ruota Movimento Confronto diinpressioni Ruota ferma e risultanti Formula della resistenza al rotolamento 1 R r mgcos α ρv 2SC z f 0 kv 2 2 Rr v m g f0 K S Cz = = = = = = = = = = Resistenza al rotolamento (N) velocità (m/s) massa del veicolo (kg) accelerazione gravitazionale (m/s2) pendenza (gradi) densità dell'aria (kg/m3) coefficiente di resistenza dei pneumatici (adimensionale) coeff. res. pneumatici in dipendenza del quadrato della velocità (s2/m2) superficie aerodinamica frontale(m2) coefficiente di portanza aerodinamica(adimensionale) Forze aerodinamiche agenti su un veicolo • Assi vento Ox’’y’’z’’ z’’ z – Fx’’ = resistenza – Fy’’ = devianza Va y’’ – Fz’’ = portanza O • Assi corpo Oxyz – F = (Xa, Ya, Za) – M = (La, Ma, Na) x x’’ y Forze aerodinamiche agenti su un veicolo nel caso bidimensionale • Deriva nulla z’’ P z F Za R x Xa x’’ Deportanza degli alettoni in auto da competizione Resistenza aerodinamica • Forza opposta al moto del corpo nel fluido, diretta secondo la velocità relativa Va. • È somma di tre contributi: – Resistenza di attrito – Resistenza di forma – Resistenza indotta Osservazioni • La resistenza di attrito è la parte di resistenza imputabile alle azioni viscose che avvengono nello strato limite • La resistenza indotta (dalla portanza) è la parte legata alla generazione della portanza • La resistenza di forma non dipende né dalle azioni viscose né dalla portanza Coefficiente CX • • È il coefficiente di resistenza aerodinamica Può essere espresso come: CX = CXa + CXf + CXi Ordine di grandezza di CXa • • • • • • Veicolo di L = 4m, a livello del mare viaggiante a 30 m/s Re = 8.260.000 Cf = 0.0036 CXa = 0.036 (S = 1/10 superficie bagnata) CX = 0.3-0.5 (maggior parte delle auto) CXa = 1/10 CX Vortici di scia • Andamento qualitativo Campo aerodinamico squareback fastback Effetto sagoma del cofano • Spostando indietro il punto C, il flusso scorre verso i lati Distribuzione delle pressioni Effetto inclinazione parabrezza e del lunotto sul CX Formula della resistenza aerodinamica 1 2 R a ρv SC x 2 Ra = Resistenza aerodinamica (N) Cx = coefficiente di resistenza aerodinamica (adimensionale) Il veicolo in salita: la forza necessaria per vincere la pendenza Baricentro mgsena d b Reazione normale anteriore c Reazione normale posteriore mgcos mg La forza necessaria al superamento della pendenza Fp mgsin α Fp = Forza necessaria al superamento della pendenza (N) La forza d’inerzia a mc = = accelerazione del veicolo (m/s2) ‘massa corretta’ (kg) o ‘massa apparente’ data da: mc m Ir Ip rp t Im rc Rr 𝜔𝑚 𝜔𝑝 𝜔𝑟 = = = = = = = = = = Fi mc a I r I p rp2 t I m rp2 rc2 R r2 momento d’inerzia delle ruote (kgm2) momento d’inerzia del ponte (kgm2) rapporto al ponte (adimensionale) rendimento di trasmissione (adimensionale) momento d’inerzia del motore (kgm2) rapporto al cambio (adimensionale) raggio della ruota (m) velocità angolare albero motore (rad/sec) velocità angolare al ponte (rad/sec) velocità angolare alla ruota (rad/sec) 𝜔𝑚 𝜔𝑝 𝜔𝑝 𝑟𝑝 = 𝜔𝑟 𝑟𝑐 = Da cosa deriva la massa corretta 𝜔𝑗 accelerazione angolare 𝑀 momenti delle forze di inerzia degli organi rotanti alla ruota 𝑗𝑅 𝑀 𝑗𝑅 = 𝐼𝑟 𝜔𝑟 + 𝐼𝑝 𝜔𝑝 𝑟𝑝 + 𝜂𝑡 𝐼𝑚 𝜔𝑚 𝑟𝑐 𝑟𝑝 𝑅 𝐹𝑖 = 𝑚 𝑎 + 𝑖 𝑗 𝜔𝑝 𝑀𝑗 𝜔𝑟 𝜔𝑚 = 𝑚 𝑎 + 𝐼𝑟 + 𝐼𝑝 𝑟𝑝 + 𝜂𝑡 𝐼𝑚 𝑟𝑟 𝑅𝑟 𝑅𝑟 𝑅𝑟 𝑅𝑟 𝑝 𝑐 𝐼𝑟 𝜔𝑟 + 𝐼𝑝 𝜔𝑟 𝑟𝑝 2 + 𝐼𝑚 𝜂𝑡 ∙ 𝜔𝑟 ∙ 𝑟𝑝 2 ∙ 𝑟𝑐 2 =𝑚𝑎+ 𝑅𝑟 𝐼𝑟 + 𝐼𝑝 ∙ 𝑟𝑝 2 + 𝐼𝑚 ∙ 𝜂𝑡 ∙ 𝑟𝑝 2 ∙ 𝑟𝑐 2 𝑎 𝐼𝑟 + 𝐼𝑝 ∙ 𝑟𝑝 2 + 𝐼𝑚 ∙ 𝜂𝑡 ∙ 𝑟𝑝 2 ∙ 𝑟𝑐 2 =𝑚𝑎+ ∙ = 𝑚 + 𝑎 𝑅𝑟 𝑅𝑟 𝑅𝑟 2 𝜔𝑝 = 𝜔𝑟 𝑟𝑝 𝜔𝑚 = 𝜔𝑝 𝑟𝑐 𝑎 = 𝜔𝑟 𝑅𝑟
Scarica