Compito d’esame del 18.07.02 Svolgimento della Sezione 5: CONTROLLORI Esempio preparato da Michele MICCIO Un processo dalla dinamica sconosciuta viene sollecitato nel set point (v. Controller Output nella parte inferiore della figura allegata) e, nella configurazione ad anello aperto, viene registrata la risposta della variabile di processo da controllare (v. curva con “rumore” nella figura allegata). a. Proporre un modello di fitting della risposta dinamica e descriverne brevemente il significato b.Determinare quantitativamente i parametri del modello di fitting c. Determinare i parametri di un controllore PI secondo il metodo IMC. rev. 2.02.05 file controllori_180702.ppt Slide 2 Step Test • • • • S teSpteTpe Tste st O peO npeLnoop L oop V a r ia b le V a r ia b le The controller is set to manual mode Process starts at steady state Controller output signal is stepped to new value Measured process variable allowed to complete response d eo d e e r:l l M C o nCt oronltlro e r:a nMu aanl uMa lo M 60 60 55 55 50 50 60 60 55 55 50 50 0 rev. 2.02.05 Step Test C o n t r o l l e r O u t pP ur to c e s s C o n t r o l l e r O u t pP ur to c e s s P ro Pc eros sc:e sCsu: sCt ou m s t oPmro Pc eros sc e s s 0 5 5 10 10 T im Te im( me in( ms )in s ) file controllori_180702.ppt 15 15 20 20 Slide 3 ° C p e r a t u r e , Step Test data h e -2 D e a d T im e (F O P D T ) F i le N a m e : h e -2 . tx t T e m M o d e l: F ir s t O r d e r P lu s 1 4 7 .5 o u t Pp ur ot ,c e % s s 1 4 5 .0 1 4 2 .5 4 0 .0 3 7 .5 3 5 .0 3 2 .5 C o n t r o lle r 1 4 0 .0 3 0 .0 0 .0 2 .5 5 .0 7 .5 1 0 .0 1 2 .5 1 5 .0 1 7 .5 T im e , m in rev. 2.02.05 file controllori_180702.ppt Slide 4 a. Modello di fitting Il modello proposto è: First Order Plus Dead Time (FOPDT) Nel dominio del tempo: dy( t ) P y( t ) K P u ( t t d ) dt Nel dominio di Laplace: GP t ds e Kp ( τ s 1) P rev. 2.02.05 file controllori_180702.ppt Slide 5 p e r a t u r e , ° C b. Determinazione dei parametri: Metodo dell’approssimazione al 1° ordine h e -2 M o d e l: F ir s t O r d e r P lu s 1 4 7 .5 D e a d T im e (F O P D T ) F i le N a m e : h e -2 . tx t T e m 146.5 o u t Pp ur ot ,c e % s s 1 4 5 .0 1 4 2 .5 1 4 0 .0 4 0 .0 3 7 .5 3 5 .0 3 2 .5 C o n t r o lle r 39 3 0 .0 0 .0 2 .5 5 .0 7 .5 1 0 .0 1 2 .5 1 5 .0 1 7 .5 T im e , m in tUstep=8.8 min tYstart=9.65 min rev. 2.02.05 file controllori_180702.ppt Slide 6 Calcolo di KP Steady State Change in the Measured Process Variable, y( t ) KP Steady State Change in the Controller Output, o( t ) y 146.5 140.0 C C KP 0.722 30 39% o % rev. 2.02.05 file controllori_180702.ppt Slide 7 Calcolo di y63.2 • y(t) starts at 140.0°C and shows a total change y = (146.5-140.0) = 6.5°C • y63.2 = ys + 0.632(y) = 140.0 + 0.632 (6.5 °C) = 144.2°C • y(t) passes through 144.2°C at t63.2 = 11.05 min rev. 2.02.05 file controllori_180702.ppt Slide 8 ° C p e r a t u r e , Analisi dei diagrammi (2) h e -2 M o d e l: F ir s t O r d e r P lu s 1 4 7 .5 D e a d T im e (F O P D T ) F i le N a m e : h e -2 . tx t T e m 146.5 1 4 5 .0 o u t Pp ur ot ,c e % s s 144.2 1 4 2 .5 1 4 0 .0 4 0 .0 3 7 .5 3 5 .0 3 2 .5 C o n t r o lle r 39 3 0 .0 0 .0 2 .5 5 .0 7 .5 1 0 .0 T im e , m in 1 2 .5 1 5 .0 1 7 .5 t63.2=11.05 min tUstep=8.8 min tYstart=9.65 min rev. 2.02.05 file controllori_180702.ppt Slide 9 Calcolo di P - The time constant is the time difference between tYstart and t63.2 - Time constant must be positive and have units of time From the plot: P = t63.2 tYstart = 11.05 9.65 = 1.4 min rev. 2.02.05 file controllori_180702.ppt Slide 10 Calcolo di td - The dead time is the time difference between tYstart and tUstep td = tYstart tUstep= = 9.65 8.8 = = 0.85 min rev. 2.02.05 file controllori_180702.ppt Slide 11 Calcoli del modulo Design Tools di CONTROL STATION® Model: First Order Plus Dead Time (FOPDT) Model Parameters: Process Gain: KP = -0.7164 °C/% Overall Time Constant: P = 1.10 min Dead Time: rev. 2.02.05 td = 0.8455 min file controllori_180702.ppt Slide 12 b. Determinazione dei parametri: Tabella finale Calcolo manuale Calcolo da Design Tools® KP, °C/% -0.722 -0.716 P, min 1.4 1.10 td, min 0.85 0.846 rev. 2.02.05 file controllori_180702.ppt Slide 13 PID Tuning Guide rev. 2.02.05 file controllori_180702.ppt Slide 14 c. Controllore PI: Determinazione dei parametri secondo IMC (1) IMC (Internal Model Control) or lambda correlations: Standard Tuning: Ideal PI Controller: c is the larger of 0.1P or 0.8 td I = P Kc rev. 2.02.05 1 p K p ( t d c) file controllori_180702.ppt Slide 15 c. Controllore PI: Determinazione dei parametri secondo IMC (2) Dai calcoli del modulo Design Tools di CONTROL STATION®: Ideal PI Controller IMC (Internal Model Control) or lambda correlations Standard Tuning Gain: KC = -1.01 %/°C direct acting Reset Time:I = 1.10 min rev. 2.02.05 file controllori_180702.ppt Slide 16
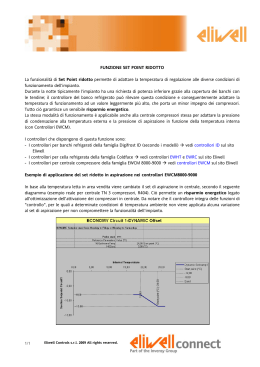
Scaricare