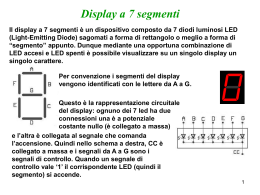
Dal sito:
www-lia.deis.unibo.it/materiale/retilogiche
Scaricate i 6 file (dec2 , mux2, mux4 con
varie estensioni).
È importante che i file siano nella stessa
cartella e che non vengano rinominati!
1
Display a 7 segmenti
Il display a 7 segmenti è un dispositivo composto da 7 diodi luminosi LED
(Light-Emitting Diode) sagomati a forma di rettangolo o meglio a forma di
“segmento” appunto. Dunque mediante una opportuna combinazione di
LED accesi e LED spenti è possibile visualizzare su un singolo display un
singolo carattere.
Per convenzione i segmenti del display
vengono identificati con le lettere da A a G.
Questo è la rappresentazione circuitale
del display: ognuno dei 7 led ha due
connessioni una è a potenziale
costante nullo (è collegato a massa)
e l’altra è collegata al segnale che comanda
l’accensione. Quindi nello schema a destra, CC è
collegato a massa e i segnali da A a G sono i
segnali di controllo. Quando un segnale di
controllo vale ‘1’ il corrispondente LED (quindi il
segmento) si accende.
2
Display a 7 segmenti
Supponiamo ora di voler visualizzare, su un display a 7 segmenti, una cifra
BCD, definita dai 4 segnali X[3..0] Il problema da risolvere è dunque
transcodificare, cioè “tradurre” il codice BCD nel codice a 7 segmenti.
Gli ingressi del transcodificatore sono i 4 segnali X[3..0]
Le uscite del transcodificatore sono i 7 segmenti a,b,c,d,e,f,g
Si considerano lecite solo le 10 configurazioni di ingresso associate alle cifre
BCD.
BCD
X[3..0]
?
7 segmenti
abcdefg
3
Transcodificatore BCD 7 segmenti
Il primo passo per creare la logica di transcodifica è avere una tabella che
descrive il funzionamento del transcodificatore.
Dec
X3
X2
X1
X0
abcdefg
0
0
0
0
0
1111110
1
0
0
0
1
0110000
2
0
0
1
0
1101101
3
0
0
1
1
1111001
4
0
1
0
0
0110011
5
0
1
0
1
1011011
6
0
1
1
0
1011111
7
0
1
1
1
1110000
8
1
0
0
0
1111111
9
1
0
0
1
1111011
4
Transcodificatore BCD 7 segmenti
Prendiamo in considerazione il segnale abcdefg cioè il segnale con codifica
7 segmenti: proviamo a scomporre il problema in 7 sotto-problemi, quindi
dobbiamo creare 7 reti per gestire altrettanti segmenti!
A questo punto l’ingresso è sempre X, però l’uscita è ad un solo bit, quindi
il problema è più semplice…
Se prendiamo come esempio il segmento a, questa è la rete che dobbiamo
progettare
BCD
X[3..0]
BCD
->
1 segmento
a
Abbiamo tanti ingressi e una sola uscita… un
MUX può esserci utile…
Possiamo cioè provare a fare la sintesi con
un mux a 16 vie.
In realtà, visto che ci sono solo dieci
configurazioni di ingresso possibili, solo 10
ingressi dovranno essere fissati a un valore
ben preciso.
Non ha importanza a quale valore logico
verranno fissati gli altri 6 ingressi “inutili”,
ma un valore dovrà essere scelto perché
nessun ingresso di una RL può essere
lasciato non connesso.
5
Astrazione
Arrivati a questo punto è necessario richiamare il concetto di astrazione e
applicarlo al nostro progetto!
Transcodificatore
Livelli di
Astrazione
Bottom-Up
Per la
realizzazione
in Quartus II
MUX e DEC
Top-Down
In fase di
progetto
Gate elementari
Transistor
In Quartus II è possibile applicare il concetto di astrazione al progetto grazie
alla creazione dei componenti di libreria (file .bsf)
6
Transcodificatore BCD 7 segmenti
1
0
1
1
0
1
1
1
1
1
Non
possono
Essere
lasciati
non
connessi
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
L’uscita del MUX è ‘a’.
‘a’ varia al variare di X, cioè è X che controlla la rete
logica. Quindi possiamo collegare X all’ingresso di
selezione del MUX e poi colleghiamo gli ingressi del
MUX a dei valori costanti 0 e 1 a seconda dei valori
della tabella che descrive il transcodificatore. X è a 4
bit allora gli ingressi del MUX saranno 2^4 cioè 16,
quindi ci serve un MUX a 16 vie.
a
X3 X2 X1 X0
Dec
X3
X2
X1
X0
a
0
0
0
0
0
1
1
0
0
0
1
0
2
0
0
1
0
1
3
0
0
1
1
1
4
0
1
0
0
0
5
0
1
0
1
1
6
0
1
1
0
1
7
0
1
1
1
1
8
1
0
0
0
1
9
1
0
0
1
1
7
Applicazione grafica del teorema di espansione partendo
da un MUX a sedici vie con le vie ancorate a costanti
Un MUX a 16 vie, con le vie ancorate a costanti è una funzione di 4 variabili
Volendo utilizzare il MUX a 4 vie che abbiamo già simulato, invece di quello
a 16, applichiamo il teorema di espansione due volte; vedremo un vantaggio
indotto dal fatto che nella nostra applicazione ci sono 6 configurazioni di
ingresso impossibili che rendono “inutili” 6 vie del MUX
Il teorema segnala che un singolo blocco a molti ingressi (molto complesso)
può essere realizzato con più blocchi con meno ingressi (meno complessi).
Infatti il teorema dice che una rete logica (RL) con n ingressi (cioè n
variabili di ingresso) può essere realizzata con due RL con n-1 ingressi più
un MUX a due vie.
Applicando ripetutamente il teorema di espansione, si arriva alla soluzione
proposta dal prossimo lucido.
Esercizio: si manipoli l’espressione generale di una funzione di due variabili
in modo da concludere che un mux a 4 vie è equivalente a tre mux a due vie
8
disposti “ad albero” (albero di Multiplexer)
Applicazione ripetuta del teorema di espansione
16
1
1
1
3
4
1
1
3
2
Effetto della
prima applicazione
2
Effetto della
seconda applicazione
2
2
2
9
Semplificazione del circuito
X1 X0
1
0
1
1
00
0
1
1
1
01
1
1
10
X0
11
X3 X2
a
Dec
X3
X2
X1
X0
a
0
0
0
0
0
1
1
0
0
0
1
0
2
0
0
1
0
1
3
0
0
1
1
1
4
0
1
0
0
0
5
0
1
0
1
1
6
0
1
1
0
1
7
0
1
1
1
1
8
1
0
0
0
1
9
1
0
0
1
1
L’ultimo MUX a 4 vie non serve poiché X3 X2
non è mai ‘11’. Inoltre il 3° MUX è sufficiente a
2 vie visto che quando X3 X2=10, X1 è fisso a
‘0’ e varia solo X0
10
Semplificazione del circuito
X1 X0
1
0
1
1
a
0
1
1
1
Questo circuito potrebbe essere
ulteriormente semplificato
sostituendo il mux a due vie con
la var X0 ma questa
semplificazione renderebbe la
rete del segmento “a” diversa
da quella degli altri segmenti
1
1
X0
3
2
1
0
X2
X3
Output Enable
11
Transcoder con ROM
Se osserviamo bene il circuito del transcoder ci accorgiamo di non aver
inventato nulla di nuovo. In realtà non c’è nemmeno bisogno di creare tale
circuito con MUX e decoder in quanto esiste già in commercio un circuito
molto simile: tale circuito è una memoria ROM (Read Only Memory).
Infatti potremmo realizzare il transcodificatore semplicemente collegando
X[3..0] all’ingresso degli indirizzi di una ROM e l’uscita della ROM direttamente
al display a 7 segmenti. Poi dobbiamo memorizzare nella ROM i valori di uscita
della tabella che descrive il transcoder, in pratica in memoria dobbiamo
inserire i valori che nel circuito di prima sono in ingresso ai MUX.
12
Utilizzo della ROM
ROM 10x7 (non esiste)
1111110
0000
0001
1
RD
abcdefg
1000
1001
Out
Servirebbe una ROM con 10 celle di
memoria (quindi 10 indirizzi descritti
da 4 bit di indirizzo) ognuna da 7 bit
ma chiaramente non esiste!
a
b
c
d
e
f
g
La ROM che più si adatta alle nostre
esigenze è una ROM con celle di
memoria da 8 bit (1byte). Per quanto
riguarda gli indirizzi, oggi non si
trovano memorie con meno di 1K
(2^10) indirizzi cioè 10 bit di indirizzo.
Addresses
X[3..0]
Gli ingressi non utilizzati sono a valore logico 0 mentre le uscite non
utilizzate sono semplicemente non connesse.
(EEP/EP/P) ROM 1024x8
X[3..0]
ADDRESS0
0
ADDRESS9
OUT0
OUT7
RD/WR*
a
b
c
d
e
f
g
Non connesso
13
Impostazioni iniziali per Quartus
Per le esercitazioni utilizzeremo Quartus II con l’interfaccia di MAX+PLUS II.
All’avvio, nel campo Look, scegliete MAX+PLUS II, oppure una volta avviato
Quartus II seguite il seguente procedimento:
Accedere alla
finestra Customize
dal menu Tools,
quindi selezionare
MAX+PLUS II nel tab
General.
14
Impostazioni iniziali per Quartus
Poi nel tab
Toolbars scegliere
Standard
MAX+PLUS II.
Lasciare il resto a
default.
15
Creazione del transcodificatore con Quartus II
I file .bdf e .bsf che avete scaricato non contengono nessuna descrizione
logica del transcodificatore, bensì tutti i componenti di libreria necessari
per realizzarlo cioè: MUX a 4 vie, MUX a 2 vie e decoder a 2 bit. Entrambi i
MUX sono con uscita tristate.
Ora è necessario creare le rete del transcodificatore con il graphic editor di
Quartus II.
16
Creare un nuovo progetto
Per creare un nuovo progetto andare in File -> New Project Wizard
Nel primo campo indicare la directory in cui verranno salvati i file del
progetto (conviene creare una cartella contenente una cartella diversa per
ogni progetto!).
Nel secondo campo indicare il nome del progetto. Il terzo campo verrà
riempito automaticamente con lo stesso nome del progetto. Cliccare Finish
17
Creazione dello schema logico
Dal menu MAX+PLUS II aprire il Graphic Editor. Utilizzando semplicemente il
Symbol Tool e il Node Tool è possibile disegnare un circuito.
Text Tool Permette di scrivere del testo
Zoom
Specchia il componente
Symbol Tool Apre la libreria per
selezionare i componenti da aggiungere
Node Tool Disegna i “fili” di
collegamento tra i componenti
Ruota il
componente
18
Aggiunta dei file al progetto
Prima di analizzare il nostro file .bdf dobbiamo specificare a Quartus quali
sono i file che compongono il nostro progetto: oltre al file appena creato dal
graphic editor, fanno parte del progetto anche i file .bdf che descrivono i
circuiti di libreria.
Prima di tutto salvate il file corrente del graphic editor.
Quindi dal menu Project cliccate su Add/Remove Files In Project e selezionate
tutti e 3 i file .bdf che avete scaricato e cliccate su Add.
Ora si può lavorare sul file .bdf del progetto inserendo i componenti di
libreria.
19
Creazione dello schema logico
La libreria interna di Quartus contiene molti componenti, sia elementari (AND,
OR, ecc…) sia più complessi, sufficienti a creare tutti gli schemi che verranno
utilizzati durante le esercitazioni.
Per prima cosa vanno piazzati i componenti utilizzando il Symbol Tool.
Premendo il relativo pulsante si aprirà una finestra nella quale si può
scegliere un componente per volta navigando tra le varie categorie (i gate
elementari sono in Primitives -> Logic).
Per aprire un componente creato dall’utente selezionare la cartella in cui è
salvato il file .bsf.
Una volta piazzati sull’area di lavoro, i componenti si possono spostare,
ruotare, specchiare e rinominare.
20
Creazione dello schema logico
A questo punto bisogna effettuare le connessioni con Orthogonal Node Tool
prestando molta attenzione ai collegamenti con gli ingressi/uscite dei
componenti. Nell’esempio possiamo vedere che il collegamento a destra è
stato effettuato correttamente mentre il collegamento a sinistra è errato.
Infatti anche se graficamente il “filo” è a contatto con l’ingresso dell’AND, il
collegamento reale non c’è!!!
Collegamento
sbagliato
Collegamento
corretto
Il Graphic Editor evidenzia con una X le terminazioni dei fili
volanti
21
Creazione dello schema logico
Finito di creare il circuito logico bisogna specificare quali sono i nodi di
ingresso e di uscita. Quartus è in grado di riconoscere in automatico solo
alcuni nodi di input e output cioè solo quelli non connessi a niente!
Nell’esempio riconosce l’uscita dell’OR come output e solo gli ingressi non
connessi degli AND come input, mentre non è in grado di riconoscere i due
ingressi centrali degli AND in quanto sono connessi tra loro!
Per l’assegnazione in automatico bisogna selezionare tutto le schema (o un
gate per volta), cliccare con il tasto destro e selezionare l’opzione Generate
Pins for Symbol Ports
22
Creazione dello schema logico
IN1, IN2 e OUT sono stati aggiunti con il procedimento descritto prima,
mentre Input_Symbol_Tool è stato aggiunto con Symbol Tool (Primitives ->
Pin) come fosse un normale componente ed è stato collegato al circuito
23
Riassumendo…
Simbolo del
componente
(bsf)
Descrizione
logica (bdf)
Editor Grafico
Analisi ed
Elaborazione
Generazione
Netlist
Forme d’onda
Simulazione
24
Analisi ed Elaborazione
Ora il circuito è finito ed è pronto per l’analisi (non la simulazione!).
Il processo testa il circuito, verifica cioè che le connessioni siano
corrette, che gli ingressi e le uscite siano nella giusta direzione, ecc… Al
termine se l’esito è Not Successful in basso verranno indicati Errors e
Warnings: leggeteli attentamente per capire dov’è l’errore! Se l’esito
invece è positivo potrete generare la netlist del circuito.
25
Netlist
La netlist è un file che contiene la lista di tutte le connessioni del circuito,
quindi è questo il file che descrive realmente il circuito!
Se il processo di Analysis & Elaboration ha avuto esito negativo o non è stato
eseguito non è possibile creare la Netlist! La generazione della Netlist si può
effettuare solo dopo un Analysis & Elaboration andata a buon fine.
Inoltre se l’analisi precedente ha avuto esito positivo ma con alcuni Warnings
allora la generazione della Netlist potrebbe non andare a buon fine, in tal caso
è necessario risolvere i Warnings e ripetere la generazione della Netlist.
La Netlist va rigenerata ogni volta che si modifica il
circuito, dopo il processo di Analysis & Elaboration.
26
Riassumendo…
Librerie .bsf
1) Processing -> Start ->
Start Analysis & Elaboration
2) Processing ->
Generate Functional
Simulation Netlist
Editor Grafico
Analisi ed
Elaborazione
Generazione
Netlist
Forme d’onda
Simulazione
27
Vector Waveform File (.vwf )
Per assegnare gli ingressi di un circuito è necessario creare un file .vwf . Per
fare ciò cliccare su File -> New e selezionare Vector Waveform File
Quindi doppio click sulla tabella
vuota a sinistra -> Node Finder…
Lasciate tutto a default,
assicurandovi che nel campo
Filter sia selezionata l’opzione
Pins: all , ora cliccate su List: vi
compariranno in automatico tutti
gli ingressi e le uscite del vostro
circuito.
Doppio
Click qui
28
Vector Waveform File (.vwf )
Selezionate i segnali che vi interessano (generalmente tutti!) e questi vi
compariranno nella schermata principale.
Una funzionalità molto comoda di Quartus II è quella di raggruppare i singoli
segnali (a singolo bit) che compongono un segnale a più bit, in un segnale
unico. Ad esempio i segnali X3 X2 X1 X0 vengono visti da Quartus come 4
segnali diversi, in realtà tutti formano l’unico segnale X. Nel file delle forme
d’onda basta selezionare i segnali che vogliamo raggruppare e con il tasto
destro selezionare Grouping… -> Group e dare un nome al nuovo segnale.
Poi dalle proprietà del segnale (sempre con il tasto destro) si può decidere
come visualizzare il valore del segnale (binary, signed decimal, unsigned
decimal…).
Risultato del raggruppamento
dei segnali X3 X2 X1 X0 nel
segnale X visualizzato in
unsigned decimal.
I segnali vanno ordinati cliccando con il destro su X e selezionando
un’opzione da Group Order (fate una prova per verificare l’ordine corretto).
Ora è sufficiente variare il valore di X per dare un valore a X[3..0].
29
Simulazione del circuito
Ora è necessario impostare l’End Time della simulazione dal menu Edit e dopo,
coerentemente, la Grid Size… (non ha senso impostare End Time= 1s e Grid
Size= 1us : avrete la griglia divisa in 1milione di parti!).
Per modificare un segnale, selezionate la parte del segnale che vi interessa e
con i comandi sulla sinistra (o con il tasto destro del mouse -> Value)
assegnategli un valore. Ora potete finalmente simulare il vostro circuito dal
menu Processing -> Start Simulation
30
Astrazione in Quartus II
Per utilizzare il concetto di astrazione in Quartus II dobbiamo creare dei
componenti di libreria (file .bsf) e quindi disegnare una nuova rete logica
utilizzando componenti di libreria sempre più complessi (Bottom-Up) fino a
che non arriveremo al nostro circuito finale senza vedere più gate elementari.
Durante la prima esercitazione abbiamo già fatto un passaggio dal livello più
basso livello di astrazione al successivo, infatti abbiamo creato un MUX e ora
abbiamo utilizzato quello stesso MUX, senza doverlo realizzare nuovamente
con AND e OR.
Un componente di libreria (in Quartus) è composto dal file .bsf che
rappresenta il disegno grafico del componente stesso e dal relativo file .bdf
che ne descrive il funzionamento.
Per prima cosa è necessario creare il file .bdf e poi andare in File ->
Create/Update -> Create Symbol Files For Current File. Verrà così creato un
file .bsf nella cartella del progetto e sarà proprio questo file che dovete
selezionare dal symbol tool nel graphic editor. Se vengono utilizzati dei
componenti di libreria .bsf, è necessario aggiungere al progetto
(Add/Remove Files In Project) i relativi file .bdf.
31