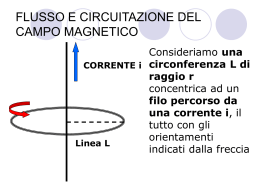
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Consideriamo una
CORRENTE i circonferenza L di
raggio r
concentrica ad un
filo percorso da
una corrente i, il
tutto con gli
orientamenti
Linea L
indicati dalla freccia
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
CORRENTE i
Linea L
B
In questo modo il
vettore B è sempre
tangente alla linea,
per cui la
circuitazione di B
lungo L può essere
calcolata in modo
semplice
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
CORRENTE i
Linea L
B
Infatti non è
necessario dividere
in parti la linea ma
la circuitazione è
solo pari al campo
B per la lunghezza
L della linea

C L ( B)  B  L
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Ma, per la legge di
Biot-Savart:
CORRENTE i
Linea L
o i
B
2 r
Inoltre:
B
L  2r
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Combinando queste cose:
o i
B
2 r
L  2r

C L ( B)  B  L
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Si ottiene:

o i
C L ( B) 
 2r
2 r
Ovvero:

C L ( B)  oi
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
i1
i2
i3
Linea L
Se una linea
abbraccia più
correnti allora al
posto di i bisogna
mettere la somma
algebrica di tutte le
correnti abbracciate
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
La formula generale prende il nome di
TEOREMA DI AMPÈRE
n

C L ( B )   o  ik
k 1
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
La circuitazione del campo magnetico non ha
lo stesso significato fisico di quella del campo
elettrico: infatti, non rappresenta un lavoro
per unità di carica e quindi non è legata agli
aspetti energetici del campo magnetico, ma è
piuttosto un utile strumento matematico per
esprimere le proprietà del campo
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
B
B
Consideriamo un
cilindro S
immerso nel
campo magnetico
costante prodotto
da un solenoide
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
B
B
Il flusso attraverso
la superficie laterale
del cilindro è nullo
in quanto il vettore
non attraversa tale
superficie
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
B
B
n
n
Il flusso attraverso
le due basi è uguale
e contrario perché
le normali sono
opposte, quindi in
un caso il coseno
dell’angolo è 1 e
nell’altro -1
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
B
B
n
n
Il flusso totale
quindi è nullo, in
quanto sommando
le varie parti queste
si cancellano a
vicenda o sono
nulle
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Questo in realtà
capita ogni volta
che le linee di
forza non si
originano da un
punto ma sono
linee chiuse o che
vanno all’infinito
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Ma questa è la
situazione generale
del campo
magnetico, in cui le
linee di forza di B
non hanno mai
origine né fine
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Possiamo quindi in generale dire che, per
una qualsiasi superficie chiusa S, il
flusso di B è nullo.

 S ( B)  0
Questo è il teorema di Gauss per il campo
magnetico
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Possiamo ora fare un confronto tra campo
elettrico e magnetico:
CAMPO ELETTRICO
CAMPO MAGNETICO

C L(E)  0

1
 S (E) 
o
n

C L ( B )   o  ik
k 1
n
Q
k 1
k

 S ( B)  0
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Possiamo comprendere l’utilità di queste
formule utilizzandole per calcolare il campo
magnetico all’interno di un solenoide.
A questo scopo consideriamo un percorso
chiuso rettangolare in cui un lato L si trova
all’interno del solenoide e gli altri all’esterno
L
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Poiché il solenoide imprigiona al suo interno
le linee di forza del campo magnetico B, dove
il campo è uniforme, per calcolare la
circuitazione occorre tener conto del solo lato
interno

C L ( B)  B  L
L
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Ma, per il teorema di Ampère, se n è il
numero di spire del solenoide allora la linea
concatena n correnti di intensità uguale i, per
cui:

C L( B)  oi  n
L
FLUSSO E CIRCUITAZIONE DEL
CAMPO MAGNETICO
Uguagliando membro a membro
B  L  oi  n
Ovvero:
n
B   oi
L