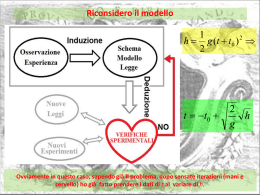
Dati caduta del grave
Per qualsiasi h,
devo rigettare l’ipotesi
Ogni corsista deve rigettare il valore atteso.
Riconsidero il modello
1
h  g (t  t0 ) 2 
2
t   t0 
2
h
g
Ovviamente in questo caso, sapendo già il problema, dopo sensate iterazioni (mani e
cervello) ho già fatto prendere i dati di t al variare di h.
Dati caduta del grave
Sul tempo abbiamo l’incertezza relativa maggiore, percui dobbiamo sceglierla come
variabile dipendente.
Attenzione a Yi (curva teorica) calcolati da A e B, da confrotarli con yi, che hanno 4 cifre
significative, percui almeno le stesse se non una in più.
Spesso ho visto rigettare dei modelli (leggi) per calcoli approssimati in modo grossolano.
Nuovo modello : h=1/2gt2 -> h=1/2g(t+t0 )2
sY < dy (medio),
modello
accettato
t   t0 
2
h
g
da B=(2/g)1/2 ottengo g = 9.9 + 0.4 m s-2
O potrei usare t0 misurato con laregressione
per ogni singola misura (studente)
1 2
h  gt
2
1
h  g (t  t0 ) 2
2
t0= -21 .+ 10 ms
Perché ci dice ciò?
• Rigore …
• Semplificazioni e sbrodolamenti.
– Approccio con media e deviazione standard
per misure ripetute e propagazione lineare
delle incertezze. Massima e minima
pendenza per la legge.
– Approccio con valore centrale
semidispersione e propagazione lineare.
Massima e minima pendenza per la legge.
Somma lineare delle incertezze, e regressione con rette di
max e min pendenza
sY < dy (medio),
modello accettato
Dalla regressione
g = 10.0 + 0.9 m s-2
e regressione
t0 = - 24 + 21 ms
confronto
g = 9.9 + 0.4 m s-2
t0= -21 .+ 10 ms
g = 10.0 + 0.9 m s-2
t0= -24 .+ 21 ms
Tutto con val. centr. e semidisp.
sY < dy (medio),
modello accettato
Dalla regressione
g = 10.2 + 1.4 m s-2
e regressione
t0 = - 29 + 33 ms
confronto
Media e dev. st. c. e
regressione lineare (MMQ).
Media e dev. st. c. e
max e min pendenza.
g= 9.9 . + 0.4 m s-2
g= 10.0 . + 0.9 m s-2
t0= -21 .+ 10 ms
t0= -24 .+ 21 ms
Val. centr., semidisp. e
max e min pendenza.
g= 10.2 . + 1.4 m s-2
t0= -29 .+ 33 ms
Se sbrodoliamo non abbiamo problemi ad accettare l’ipotesi,
ma potremmo essere poco risolutivi per rifiutarne un’altra
Esempi a costo zero
• Pendolo, potete farlo a casa, provate a
verificare se T=T(l) o T=T(l1/2) o T2= T2(l)
• Provare con bilia o cilindro su un tavolo
inclinato
Siete in grado di rigettare la legge del punto
materiale (a=gsinq)?
Fate l’analisi a priori, per vedere di quanto sollevare il tavolo, per
risolvere bene e non avere bilie, che rotolano troppo rapidamente.
Indicazioni
Provate a fare
Prima l’analisi a
priori
Piano di un
tavolo 170 cm,
Spessori sotto il
tavolo da
decidere sulla
base dell’analisi
NUOVO ESEMPIO
IL CALORIMETRO un modellino semplici, un problema di gestione dell’esperienza.
Modello
Ma Massa d’acqua a T0,
Corpo mx cx a T1
Voglio utilizzarlo per misura cx
• Analisi a priori:
• 50 g di alluminio, cx=0.208 cal g-1 K-1 , si
raggiungerebbe una t di equilibrio
Misura con Alluminio
mx= 497.27 g, Ma= 854.36 + 0.02 g,
Misure di T con termocoppia:
Teb=T1=98.1 °C, To=18.2 °C, Tequ=22.7 °C.
Risulta:
cx=0.189 + 0.003 ca , valore atteso 0.214 ca
Devo ritornare sul modello
Calibrazione
Ritorno sui dati con la calibrazione
Confronto con valore atteso
Calore specifico: Alluminio e Ferro
A 20 °C la mia misura è
0.2082 calorie.
Altre problematiche: osservando il corpo scaldato in acqua, si osserva che è bagnato.
Evaporazione, o quantità di acqua calda introdotta?
Che fare?
• Organizzarsi con corpi di massa maggiore.
• Calibrare allo stesso livello di acqua.
• Scaldare il corpo in un tubo di ottone, chiuso
chiuso in fondo ed immerse nell’acqua bollente.
• Nell’immediato dimensionare un riscaldatore e
misurare il calore specifico dell’acqua.
• Anche utile per la connessione con
• V=RI, P=VI
Misura di ca con riscaldatore
Q=mca DT
Q=Pt=VIt
Misura di ca con riscaldatore
Misura di h con LED
• eVa energia di soglia per mandare gli e- in
banda di conduzione, l’elettrone ricasca
nella lacuna e quindi riemette un fotone.
• eV proporzionale ad hn
Misurare per LED di vari colori la tensione,
oltre la quale si osserva I>0
Dati presi all’Ariosto
Osservazione da fisico: incertezza su l?
Trova V percui I=0?
I[mA]
I vs V
Infrarosso
Blu
1100
y = 4638.1x2 - 24599x + 32558
900
y = 59354x2 - 110877x + 51726
700
500
300
100
0,001
-100
0,001
0,002
0,002
0,003
0,003
V [V]
I vs V
y = 68834x2 - 228680x + 189891
585 nm
I[mA]
1100
660 nm
635 nm
560 nm
y = 47903x2 - 147376x + 113336
900
y=
33812x2
- 114511x + 96931
y = 39333x2 - 121683x + 94086
700
500
300
100
0,001
-100
0,001
0,002
0,002
0,002
0,002
0,002
0,002
0,002
0,002
V [V]
0,002
Ho fatto un regressione, che chiamerei semigrafica, con excel, quando il polinomio
di grado due approssima bene i dati ed attraversa lo zero in y lo accetto.
Risolvo l’equazione di 2° grado del polinomio fornito da excel per I=0 ed ottengo Va
Ho usato le incertezze su lambda uguali ai LED, acquistati da me, per i quali
ho le specifiche.
Per la regressione V= V(1/l) ho un altro problema, l’incertezza relativa su 1/l è
superiore a quella su V.
Soluzioni:
Utlizzare per la misura delle tensioni una scala tale da avere un incertezza
Confrontabile con quella di 1/l.
Fare l’analisi di 1/l in funzione di V.
Ho usato le incertezze su l uguali ai LED, acquistati da me, per i quali
Ho le specifiche, trovato B con excel ed usato per propagare su yi l’incertezza di xi.
Si vede che la legge non è
appropriata per i dati …
Possiamo comunque fornire una misura
Ci troviamo in questa situazione:
8.50
t [s]
Se s Y  dy
8.00
dY  s  dy 
7.50
2
Y
7.00
Sconto per le superiori
6.50
6.00
1.50
2.00
2.50
3.00
n
3.50
Non accettiamo la legge
dYi  s Y  dyi
Forniamo comunque una stima
2
Trova Va invertendo gli assi,
polinomiale di grado 5 …
ma con dY -> OK
Anche in questo caso osserverei che sY > dye dovrei ricalcolare B con con l’incertezza
dY=sY+dy, percui l’intervallo di fiducia risulterebbe maggiore e quindi OK.