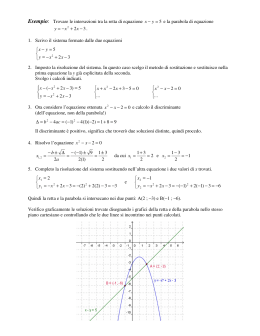
SESSIONE ORDINARIA 2007
CORSO DI ORDINAMENTO
SCUOLE ITALIANE ALL’ESTERO - AMERICHE
PROBLEMA 1
Si consideri la funzione f definita da f ( x )  1  x 2 , il cui grafico è la parabola  .
1. Si trovi il luogo geometrico  dei centri (a, b) delle circonferenze che sono tangenti a 
nel suo punto di ascissa 1.
2. Si calcoli l’area del dominio piano delimitato da  e da  .
1
3. Si tracci il grafico della funzione .
f
4. Si considerino i due domini piani, ricadenti nel III e IV quadrante, determinati dai grafici di f
1
e di
nella striscia 2  y  1 e se ne calcoli l’area.
f
Svolgimento
1. Il luogo geometrico  dei centri (a, b) delle circonferenze che sono tangenti a  nel suo punto
1
1
di ascissa 1 è la retta di equazione y  x  . Essa è la perpendicolare alla tangente alla parabola
2
2
nel suo punto di ascissa 1.
1
1
2. La retta di equazione y  x  incontra la parabola nel punto di ascissa 1 e nel punto di ascissa
2
2
3

L’area del dominio piano delimitato da  e da
 si ottiene con l’integrale
2
1
1
1
125
1
2
1

x
dx

3
3  2 x  2  dx e vale 48 .


2


2
3. Il grafico della funzione
1
è il seguente:
1  x2
1
4. Ciascuno dei due domini piani, ricadenti nel III e IV quadrante, determinati dai grafici di f e di
1
ln 2
2
nella striscia 2  y  1 ha area
2 3
1  3 3  0,89 , ottenuta calcolando:
f
2
3

2
1
 1  x2 dx 
6
3

3
 1  x  dx   2dx .
2
2
2
6
2
PROBLEMA 2
Della parabola  si sa che passa per i punti A(0, 2) e B(2, 0) , ha l’asse parallelo all’asse y e volge
la concavità nel verso negativo di tale asse; inoltre l’area del dominio piano delimitato da  e dai
10
segmenti OA e OB è
.
3
1. Si determini l’equazione di  e se ne tracci il grafico.
2. La retta s di equazione y  mx  2 , dove m è un parametro reale, interseca  in A e in C. Si
esprimano in funzione di m le coordinate di C.
3. Si studi la funzione f (m)  AC 2 e se ne tracci il grafico  .
4. Si dica quale posizione assume la retta s in corrispondenza dell’estremo relativo della curva  .
Svolgimento
1. La parabola  ha equazione y   x 2  x  2 . Si ottiene imponendo il passaggio per A, per B e,
2
successivamente, risolvendo l’equazione, in a,
10
  ax   2a  1 x  2  dx  3 .
2
0
2. Il punto C, in cui la retta s di equazione y  mx  2 interseca la parabola  , oltre A, ha


coordinate C (1  m), (  m 2  m  2) .
3. La funzione f (m)  AC 2 è f (m)  (1  m)2 (1  m 2 ) . Essa non ha massimo è ha un minimo
(relativo e assoluto) nel punto (1,0). Il suo grafico è il seguente.
2
4. Per m = 1 si ha la retta che determina il segmento il cui quadrato è minimo. L’equazione di tale
retta è: y  x  2 .
QUESTIONARIO
QUESITO 1
Si dimostri che fra tutti i triangoli rettangoli aventi la stessa ipotenusa, quello isoscele ha l’area
massima.
Svolgimento
I triangoli rettangoli di data ipotenusa sono tutti inscritti in una semicirconferenza che ha come
diametro l’ipotenusa stessa. Se indichiamo con 2r l’ipotenusa-diametro, e con x l’angolo formato da
1
un cateto e con l’ipotenusa, l’area del triangolo ha espressione y  r sin x cos x = sin 2 x , che è
2


massima quando 2 x  , ovvero x  .
2
4
QUESITO 2
Quando due rette si dicono sghembe? Come si definisce la distanze tra due rette sghembe?
Svolgimento
Due rette si dicono sghembe se non esiste un piano che le contiene entrambe (e quindi non hanno
punti in comune, appartenendo a piani diversi).
Se r ed s sono due rette sghembe, fra le infinite rette che congiungono un punto dell’una con un
punto dell’altra esiste solo una retta perpendicolare ad entrambe; il segmento che si individua su
questa perpendicolare comune, che è minore di tutti gli altri segmenti che hanno i due estremi su di
esse, si dice distanza fra r ed s.
QUESITO 3
Si calcolino le radici dell’equazione: 3x 3  9 x 1  10 .
Svolgimento
3
Se si pone 3x  t si ottiene l’equazione 9t 2  27t  10  0 , con t>0, che ha una radice negativa1
quindi non accettabile- e una t  , da cui si ricava x = -1.
3
QUESITO 4
Si traccino i grafici delle seguenti funzioni di  in  :
x
f : x  3x 1; g : x  3x  1; h : x  3 ; k : x  3 x
Svolgimento
Sono tutti grafici che si ottengono per traslazione, o simmetria, dal grafico della funzione
esponenziale y  3x .
QUESITO 5
Siano a b due numeri positivi diversi da 1. S i dimostri che log a b  log b a  1 .
Svolgimento
Si usano le proprietà dei logaritmi (per esempio quella del cambiamento di base).
QUESITO 6
Il coefficiente angolare della tangente al grafico della funzione f(x) è, in ogni suo punto P, uguale al
quadruplo della radice cubica dell’ascissa di P. Si determini f(x), sapendo che il grafico passa per il
punto A(1, 0) .
Svolgimento
3
È y '  4 3 x , da cui y   4 3 xdx . Si ottiene f ( x )  y  x 3 x  1 .
4


QUESITO 7
Un cerchio ha raggio 1 metro. Quanto misura il lato del decagono regolare in esso inscritto? E qual
è la misura del lato del decagono regolare circoscritto?
Svolgimento
Se ogni lato del decagono inscritto è visto come corda in una circonferenza, l’angolo al centro
corrispondente è di 36°, e quindi quello alla circonferenza è di 18°. Per il teorema della corda,
5 1
5 1
quindi, si ha l10  2sin18  2

.
4
2
Costruendo due opportuni triangoli, si trova che il lato del decagono circoscritto è L10  2 tan18 =
2 25  10 5
.
5
QUESITO 8
1
1
1
 1
Il valore della seguente espressione  arccos xdx   1  2 arcsin x  dx è
. Spiegarlo in
20
2
0
maniera esauriente.
Svolgimento
Non è necessario il calcolo dei singoli integrali (peraltro piuttosto complesso).
Per la proprietà additiva degli integrali definiti:
1
1
1
1
1

arccos
xdx

(1

2
arcsin
x
)
dx

 arccos x  arcsin x   dx . Ma, per definizione, il coseno è
0


20
2
0
la cofunzione del seno (cioè il seno del complementare), quindi arccos x  arcsin x 

. L’integrale
2
4
1
si riduce, perciò, a:

1
  2  2  dx . Per il significato di integrale definito esso è immediatamente
0
uguale a
 1
 (un rettangolo con base uguale a 1 ha area uguale, in valore numerico, alla sua
2 2
altezza).
5