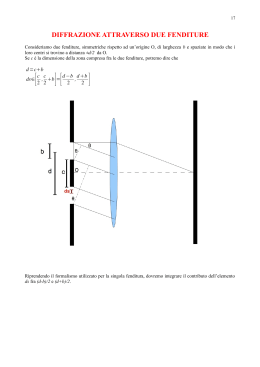
N.Giglietto A.A. 2004/05- 37.3-4 - Massimi e minimi di
diffrazione singola fenditura -
1
'
$
Cap 37 - Ottica Fisica- Diffrazione
Se un’onda incontra un ostacolo di dimensioni
confrontabili con la sua lunghezza d’onda, l’onda si diffrange (o si sparpaglia). In alre parole la
diffrazione è un particolare fenomeno d’interferenza che si verifica quando un’onda incontra un
ostacolo lungo il suo percorso. Ad esempio la diffrazione avviene quando un’onda luminosa passa attraverso una fenditura, ed è un fenomeno
caratteristico di tutte le onde.
37.2 - Diffrazione da singola
fenditura
Consideriamo la situazione di attraversamento
della fenditura e vediamo quando si verificano
gli effetti d’interferenza. Rispetto alla trattazione dell’interferenza stiamo considerando la presenza di un unica fenditura. Assumiamo che il
fronte d’onda piana attraversi una fenditura sottile (rettangolare) di lunghezza a. Ricordiamo
che in questi casi si può applicare il principio di
Huygens-Fresnel e considerare ogni punto della
&
1
%
N.Giglietto A.A. 2004/05- 37.3-4 - Massimi e minimi di
diffrazione singola fenditura -
2
'
$
regione nella fenditura come sorgente puntiforme
di onde sferiche. Dividiamo l’intera fenditura in
due parti e consideriamo la differenza di fase delle onde emesse ai due estremi della metà fenditura quando arrivano sullo schermo nel punto P1 in
figura.
La differenza di cammino tra le due onde è a2 sinθ.
Pertanto come nel ragionamento fatto per l’interferenza questa differenza di cammino comporta una differenza di fase che può essere distruttiva o costruttiva. Nel primo caso si
ha il primo minimo quando a2 sinθ = λ2 ovvero asinθ = λ. Il ragionamento fatto possiamo
ripeterlo considerando l’ulteriore metà fenditura che porterà a trovare un secondo minimo: in
&
%
2
N.Giglietto A.A. 2004/05- 37.3-4 - Massimi e minimi di
diffrazione singola fenditura -
3
'
$
questo caso la condizione che risulta considerando un quarto della fenditura è a4 sinθ = λ2 ovvero
asinθ = 2λ. Iterando il ragionamento si ottiene
quindi che i minimi sono definiti dall’equazione
asinθ = mλ con m=1,2,3. . . I massimi e minimi
d’interferenza hanno però una intensità variabile. Nel paragrafo seguente effettueremo il calcolo
quantitativo. Notiamo comunque che l’effetto è
evidente quando la lunghezza d’onda è paragonabile alla dimensione della fenditura. Inoltre al
centro della fenditura tutte le onde si compongono con differenza di fase nulla per cui la posizione centrale avrà necessariamente un massimo
d’interferenza.
37.3-4 - Massimi e minimi di
diffrazione singola fenditura
Dividiamo la fenditura in N parti di lunghezza
∆x piccole a sufficienza da considerarsi puntiformi. Dal momento che ∆Φ = 2π
λ ∆(cammino)
la differenza di fase allora in base a quanto trovato prima, la differenza di fase tra le due on&
3
%
N.Giglietto A.A. 2004/05- 37.3-4 - Massimi e minimi di
diffrazione singola fenditura -
4
'
$
de elementari adiacenti (e distanti ∆x) è ∆Φ =
2π
λ ∆xsinθ. E ogni onda adiacente ha la stessa
ampiezza ed è sfasata di questa quantità con la
precedente. Se ripetiamo il calcolo con la notazione dei fasori otteniamo la situazione descritta
dalla figura:
Nella figura, al tendere ad infinitesimi dei segmenti ∆x
allora i fasori di ogni tratto tendono a descrivere
un arco di circonferenza di raggio R. L’angolo φ
in figura è lo sfasamento tra il primo e l’ultimo
segmento ed è anche l’angolo al centro della circonferenza. Il campo risultante Eθ è dalla figura
pari a Eθ = 2Rsin( φ2 ) inoltre l’angolo espresso
in radianti è (θ = Rs ) φ = ERm . Utilizziamo quest’ultima equazione per eliminare l’arbitrario va&
4
%
N.Giglietto A.A. 2004/05- 37.3-4 - Massimi e minimi di
diffrazione singola fenditura -
5
'
$
lore di R in questa figura e otteniamo che l’ampiezza risultante è Eθ = ( Eφm )sin( φ2 ) Da questa
2
quindi elevando al quadrato otteniamo che l’inEθ2
I
tensità prodotta dalla diffrazione è Im = E 2
m
2
Im ( sinα
)
α
da cui I =
con α = φ/2. L’angolo φ
che abbiamo indicato infine sarebbe l’angolo di
sfasamento tra il primo e l’ultimo dei segmenti
e quindi degli estremi della fenditura: lo sfasamento per questi è allora φ = 2π
λ asinθ
Di conseguenza la condizione per i minimi si ha
quando α = mπ, m=1,2,3. . . che significa quando l’angolo di inclinazione sullo schermo è dato
da α = φ/2 = πa
λ sinθ = mπ da cui asinθ = mλ.
&
%
5
N.Giglietto A.A. 2004/05-
37.5-Diffrazione da foro circolare
-
6
'
$
(sin(3.15*(sin(3.15*x/180)))/(3.15*sin(3.15*x/180.)))^2
1
0.8
0.6
0.4
0.2
0
-80
-60
-40
-20
0
20
40
60
80
Angolo (gradi)
Figura 1: Due esempi di diffrazione per a=λ e
per a=2λ
La distanza tra i primi due minimi attorno al
centro (m=± 1) è pari a ∆sinθ = 2λ
d . Questo parametro ci da una indicazione quantitativa di come e quando funziona la diffrazione: per
a À λ sinθ → 0 e si osserva una fenditura stretta illuminata questo è il caso usuale in cui non vi
sono effetti diffrattivi. Quando invece al limite
a = λ i due minimi si trovano a 90◦ , il che comporta tutto lo schermo illuminato (e a maggior
ragione per a≤ λ. La determinazione dei massi&
6
%
N.Giglietto A.A. 2004/05fenditura -
37.6 Diffrazione da doppia
7
'
$
mi è più complessa anche se con buona approssimazione si trovano massimi quando l’argomento
λ
sin2 è max che comporta sinθ = (2m + 1) 2a
37.5-Diffrazione da foro circolare
L’analisi dettagliata di questa situazione è più
complessa anche se il metodo di calcolo è sostanzialmente il medesimo. Il risultato è pertanto simile a parte un coefficiente che viene dal calcolo
dettagliato e che dipende dalla geometria specifica. La condizione per trovare il primo minimo è dato dall’equazione sinθ = 1.22 dλ d=2R
diametro del foro.
Potere risolvente degli strumenti
ottici
Negli strumenti ottici è importante risolvere le
immagini, ovvero distinguerle. Supponiamo ad
esempio di avere due sorgenti luminose e puntiformi e separate angolarmente di un certo angolo teta. Nella situazione ideale lo strumento
evidenzia le due sorgenti e su un ipotetico schermo troveremmo due massimi distinti. Tuttavia
&
7
%
N.Giglietto A.A. 2004/05fenditura -
37.6 Diffrazione da doppia
8
'
$
se teniamo conto che possono comparire effetti
di diffrazione allora dobbiamo stabilire prima di
tutto un criterio per decidere quando due sorgenti sono distinte. Alla luce di quanto detto
prima, infatti, ogni fenditura circolare (anche la
lente ne è un esempio) diffrange e rispetto alla
posizione centrale, la larghezza dell’immagine è
pari alla larghezza del massimo centrale di diffra-
zione.
Due immagini
sono distinte (angolarmente) se il massimo della seconda sorgente è quantomeno posizionato
in corrispondenza del minimo della prima, o più
lontana (Criterio di Rayleigh). Utilizzando
la precedente equazione delle fenditure circolari questo comporta che la separazione angolare
&
8
%
N.Giglietto A.A. 2004/05fenditura -
37.6 Diffrazione da doppia
9
'
$
deve essere almeno θR = 1.22 λd Pertanto anche
per le lenti non si può prescindere dai limiti imposti dalla diffrazione che impedisce di separare
all’infinito gli oggetti. Tale limite quindi affetta
sia i microscopi che i telescopi. Per i miscroscopi
un modo di aumentare la risoluzione è quello di
utilizzare lunghezze d’onda più corte
37.6 Diffrazione da doppia
fenditura
Nella situazione di doppia fenditura si combinano i due effetti soprattutto quando la fenditura
ha dimensioni comparabili alla lunghezza d’onda. L’effetto combinato di interferenza e diffrazione si pu pensare combinato in termini matematici come inviluppo della curva dell’interferenza con quella della diffrazione. La seguente
figura fornisce un’idea immediata di come funziona la combinazione dei due effetti: in a) è
la sola interferenza delle due fenditure, in b) la
diffrazione di una singola ed in c) l’effetto combinato. Potete anche vederlo come un segnale
&
9
%
N.Giglietto A.A. 2004/05-
37.7 Reticoli di diffrazione
-
10
'
$
modulato su un altro.
La formula che descrive questa situazione dell’intensità sullo schermo è la seguente:
sinα 2
I = Im (cos β)(
)
α
2
πa
con β = πd
sinθ
e
α
=
λ
λ sinθ che evidenzia
i due termini rispettivamente di interferenza e
diffrazione. Dalle formule ritroviamo che nel limite che a → 0 il termine sinα
α → 1 ed il tutto
tende all’interferenza di doppie fenditure (sotti&
10
%
N.Giglietto A.A. 2004/05-
37.7 Reticoli di diffrazione
-
11
'
$
li). Notare che in questo caso c’è anche l’effetto
di diffrazione anche se nell’introduzione al capitolo precedente l’effetto l’abbiamo denominato
interferenza. Pertanto Interferenza e diffrazione sono da vedersi come fenomeni intimamente
correlati.
37.7 Reticoli di diffrazione
L’evoluzione del discorso precedente si ha quando si parla di N fenditure, o nella analoga situazione in riflessione su incisioni regolarmente
spaziate. Quando si ha un gran numero di fenditure le curve dei massimi di luce, che prima abbiamo visto per due fenditure, si stringono sempre più sino a diventare righe Possiamo anche in
questo caso calcolare le condizioni di max e min
d’interferenza. Indichiamo con d il passo del reticolo ovvero la distanza tra due solchi/fenditure
&
%
11
N.Giglietto A.A. 2004/05risolvente -
37.8 Reticoli:dispersione e potere
12
'
$
consecutivi
In analogia a quanto trovato per l’interferenza,
sul punto dello schermo in P avremo che l’interferenza è costruttiva se dsinθ = mλ m =
0, 1, 2, . . . è detto in questo numero d’ordine in
cui m=0 corrisponde al massimo centrale. Se
risolviamo questa eq. rispetto l’angolo otteniamo θ = arcsin( mλ
d ) che è un eq. che può essere
utilizzata per misurare la λ con misure di angoli (nel caso della doppia fenditura i massimi
si sovrappongono troppo per poter utilizzare lo
stesso metodo).
Larghezza delle righe
Se consideriamo come larghezza della righa la
&
12
%
N.Giglietto A.A. 2004/05risolvente -
37.8 Reticoli:dispersione e potere
13
'
$
distanza tra un max ed un minimo d’interferenza allora possiamo vedere cosa determina la larghezza delle righe nei reticoli. Nella trattazione
della diffrazione (e anche questa ne è un esempio) abbiamo visto che si hanno minimi quando
gli estremi della fenditura hanno una differenza di fase distruttiva: per la singola fenditura
questa condizione è asinθ = λ nel caso di N
fenditure le fenditure estreme saranno spaziate
di N dsin(∆θ) considerando un massimo centrale, l’angolo cui troveremo il minimo ∆θ = Nλd
è quello corrispondente alla larghezza del picco. Per N molto grande quindi i picchi di massimo diventano delle righe come indicato in fi-
gura
&
La
%
13
N.Giglietto A.A. 2004/05diffrattive -
Altre applicazioni CD, lenti
14
'
$
formula precedente si estende a tutti i massimi
λ
con inclinazione θ secondo ∆θ = Ndcosθ
37.8 Reticoli:dispersione e potere
risolvente
Se utilizziamo i reticoli con luce non monocromatica possiamo essere interessati a distinguere
i massimi di dur lunghezze d’onda vicine. In
questi casi dobbiamo definire una quantità che
ci misuri il grado di separazione. Questa quan∆θ
tità è detta dispersione D = ∆λ
tanto più
grande è D tanto più lontane angolarmente sono
due righe separate di lunghezze d’onda distanti
m
∆λ. Dimostriamo brevemente che D = dcosθ
infatti partendo dalla condizione dei massimi:
dsinθ = mλ e differenziamo entrambi i membri
dθ
m
dcosθdθ = mdλ da cui dλ
= dcosθ
che coincide
con D se coinsideriamo variazione finite piccole.
Potere risolvente
Quando siamo interessati soprattutto a distinguere due lunghezze d’onda vicine allora si deλ
si può difinisce il potere risolvente R = ∆λ
&
14
%
N.Giglietto A.A. 2004/05diffrattive -
Altre applicazioni CD, lenti
15
'
$
mostrare che R = N m In definitiva un gran numero di fenditure aumenta il potere risolvemte
del reticolo e la dispersione.
Altre applicazioni CD, lenti
diffrattive
Una applicazione è quella dei Compact Disk nei
quali un raggio laser colpisce una superficie di
alluminio con delle incisioni lungo le tracce disposte a spirale. I solchi (delle buche in pratica)
producono interferenza in riflessione. Da quanto
abbiamo visto prima si hanno delle righe o buio
e questo si può interpretare secondo un sistema
binario come alternanza di bits. Un altra applicazione è quella delle lenti di Fresnel in cui si
usa un opportuno reticolo diffrattivo in trasmissione per realizzare un ingrandimento angolare.
Infatti dal momento che si hanno massimi di un
certo ordine e a certi angoli si può realizzare un
reticolo che funzioni come lente senza utilizzare
la rifrazione. Un grosso vantaggio di questo tipo di lente è che si può realizzare una lente di
grosse dimensioni e leggera (ad esempio usando
plastiche), mentre le normali lenti sono necessariamente in vetro e spesse (perche’ sono superfici
curve). Esempi di queste lenti sono comunemente in commercio (le lenti dei laser impiegate nei
lettori cd sono di questo tipo) o utilizzate quali lenti d’ingrandimento o lenti particolari come
quelle dei fari vedi ad es.
&
15
%
N.Giglietto A.A. 2004/05diffrattive -
Altre applicazioni CD, lenti
16
'
$
http://www.qsl.net/ari_trieste/Lighthouse/Lighthouseita.htm
Figura 2: La lente del faro di Trieste
&
%
16