C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Appendice A
Richiami di calcolo vettoriale e tensoriale
Scopo dell’ Appendice
Ricapitolazione dell’algebra e del calcolo vettoriale e tensoriale e dei relativi teoremi di calcolo integrale
Utile per riferimento.
Indice dell’Appendice
Paragrafo
A.1
A.2
A.3
A.4
A.5
A.6
A.7
A.8
A.9
A.10
A.11
Generalità
Prodotti
Prodotti di tre vettori
Sistemi di riferimento
Differenziazione dei vettori
Calcolo differenziale
A.6.1 Operatore nabla
A.6.2 Fattori di scala
A.6.3 Gradiente
A.6.4 Divergenza di un campo vettoriale
A.6.5 Significato fisico della divergenza del campo di velocità
A.6.6 Rotore di un campo vettoriale
A.6.6.1 Significato fisico del rotore:
Operatori differenziali del secondo ordine
A.7.1 Laplaciano
Algebra tensoriale
A.8.1 Prodotto scalare tra un vettore ed un tensore
A.8.2 Doppio prodotto tra tensori
A.8.3 Analisi spettrale di tensori
Tensori di interesse in Fluidodinamica
A.9.1 Tensore degli sforzi
A.9.2 Gradiente della velocità
Elementi di calcolo integrale
Cenni sui sistemi di coordinate curvilinee non ortogonali
A.11.1 Assi reciproci
A.11.2 Componenti controvarianti e covarianti
A.11.3 Variazione delle componenti di un vettore in sistemi curvilinei ruotati
A.11.4 Il tensore metrico
pagina
2
3
6
6
8
9
9
10
11
11
12
12
13
14
14
16
17
18
18
20
20
21
26
27
30
32
34
36
A.1
C.GOLIA – Fluidodinamica
A.1
Appendice A - Richiami di Calcolo vettoriale e tensoriale
GENERALITÀ
Le grandezze fisiche in ogni punto R di uno spazio a n dimensioni (esempio n=3) si possono classificare
come:
•
•
•
scalari (tensori di ordine 0) che sono determinati da n0=30=1 componente scalari
vettori (tensori di ordine 1) che sono determinati da n1=31=3 componenti scalari
tensori (tensori di ordine 2) che sono determinati da n2=32=9 componenti scalari
Esempi di scalari sono i campi di temperatura, di densità,… che sono determinati, per ogni punto, soltanto
dalla intensità, cioè da un numero, in questo contesto gli scalari saranno indicati da una lettera.
Esempi di vettori sono i campi di forze, di velocità, ecc. che, per ogni punto, sono determinati da un’intensità
e da una direzione, in questo contesto i vettori saranno indicati con lettere sottolineate ( a, V,F,…).
Esempi di tensori sono i prodotti d’inerzia, il tensore degli sforzi, ecc.. che, per ogni punto, sono
determinati da un valore di intensità, e da due direzioni (per il tensore degli sforzi sono tipicamente la
normale al piano su cui agisce lo sforzo superficiale e la direzione dello sforzo superficiale), in questo
contesto i tensori saranno indicati con simboli sottolineati due volte (τ , S , Ω …).
I campi vettoriali e tensoriali sono spazi di Hilbert, cioè spazi normati in cui è definito un prodotto scalare,
il quadrato della norma (intensità o modulo del vettore) è definito come il prodotto scalare di un vettore con
se stesso a 2 = a • a , in questo contesto il modulo di un vettore a è indicato con il simbolo non sottolineato:
a = a•a
(A.1)
La direzione di un vettore a è data da un versore ea (cioè da un vettore di intensità unitaria) pari al rapporto
del vettore sul suo modulo:
a
a
ea = =
(A.2)
a
a •a
In definitiva si potrà rappresentare il vettore a come prodotto del modulo ”a” e della direzione “ea”:
a = a e a = (a • e a ) e a
In un comune spazio vettoriale ( a 3 dimensioni) il prodotto scalare
a•b di due vettori a e b è definito come il prodotto dei moduli
moltiplicato il coseno dell’angolo formato tra i due vettori.
Due vettori sono ortogonali se il loro prodotto scalare è nullo.
La componente di un vettore a lungo una direzione indicata dal versore
n è data dal prodotto scalare di a n ≡ a • n .
(A.3)
a•b = a b cosβ
b
a
β
b cosβ
Con tale bagaglio è immediato costruire la rappresentazione di vettori
in un sistema coordinato.
Noi considereremo soltanto sistemi ortogonali, cioè sistemi di riferimento definiti da tre direzioni ortogonali
tra di loro.
A.2
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
z
Il più semplice è il sistema cartesiano, definito dai versori i,j,k
che indicano rispettivamente le direzioni degli assi coordinati
x,y,z.
E' importante notare che queste direzioni coordinate, e quindi i
versori sono gli stessi per tutti i punti dello spazio (cioè non
variano nel campo).
In questo sistema un vettore è indicato come somma delle
componenti scalari lungo i tre assi coordinati moltiplicate i
rispettivi versori:
a
k
j
az
y
i
ax
x
ay
( )
a = (a • i ) i + a • j j + (a • k ) k = a x i + a y j + a z k
(A.4)
E’ ovvio che la somma di vettori viene fatta con la regola del parallelogramma, da cui ne discende che la
rappresentazione della somma di due vettori mediante le componenti coordinate è fatta sommando le
rispettive componenti.
[
( )
j + a k ] + [b
] [
]
] i + [a + b ] j + [a
( )
a + b = (a • i ) i + a • j j + (a • k ) k + (b • i ) i + b • j j + (b • k ) k =
[
= ax i + ay
z
x
]
i + b y j + b z k = [a x + b x
y
y
Ovviamente il prodotto di uno scalare “s” con un vettore “a” sarà pari al vettore
le cui componenti scalari sono moltiplicate per “s”:
( )
[ ]
s a = s(a • i ) i + s a • j j + s(a • k ) k = [sa x ] i + sa y j + [sa z ] k
A.2
z
(A.5)
+ bz ] k
a
(A.6)
b
a+b
Prodotti
I prodotti tra vettori a e b possono essere di tre tipi:
•
•
•
scalare (o interno)
vettoriale
tensoriale (o diadico)
a•b
a∧b
ab
Attenzione: altre simbologie sono usate in letteratura per indicare tali prodotti!
Il prodotto scalare di due vettori, a e b , è stato già definito, in un comune spazio vettoriale (a 3
dimensioni) come lo scalare dato dal prodotto dei moduli dei due vettori moltiplicato per il coseno
dell’angolo formato tra i due vettori.
Il prodotto scalare di due vettori viene fatto, di solito, mediante somma dei prodotti delle componenti.
In una rappresentazione cartesiana i prodotti scalari dei versori diversi tra di loro sono nulli (in quanto
ortogonali), quelli dei versori con se stessi sono ovviamente unitari:

1 se i = j 
e i • e j = δ ij =

0 se i ≠ j 

(A.7)
A.3
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
ovvero:
i•i =1
; i• j= 0 ; i•k = 0
j• i = 0 ;
j• j = 1 ;
j• k = 0
(A.8)
k •i = 0 ; k • j = 0 ; k •k =1
ne discende la comoda rappresentazione:
[
][
]
] i • k + [a
a • b = a x i + a y j + a z k • bx i + by j + bz k =
[
]
= [a x b x ] i • i + a x b y i • j + [a x b z
[
]
[
]
+ a y b y j • j + a y b z j • k + [a z b x
[
]
= [a x b x ] + a y b y + [a z b z ] =
]
] k • i + [a
y
bx j• i +
z
]
b y k • j + [a z b z ] k • k =
(A.9)
= a x bx + a y by + a z bz
E’ facile rilevare che il prodotto scalare:
•
•
•
È commutativo, i.e.
E’ distributivo, i.e.
Non è associativo, i.e.
a•b = b•a
a • [b + c] = a • b + a • c
a [b • c] ≠ [a • b]c
Applicazioni tipiche del prodotto scalare in meccanica sono rappresentate dal calcolo del lavoro dL di una
forza F a seguito di uno spostamento elementare ds: dL = F•ds ; ovvero dalla portata dQV di un campo
vettoriale V attraverso una areola dA di normale n: d QV= V•n dA.
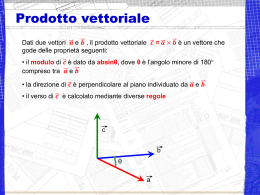
Il prodotto vettoriale è definito come il vettore che ha come
intensità il prodotto dei moduli per il seno dell’angolo formato
ed è normale al piano formato dai due vettori, la direzione del
prodotto vettoriale dipende dal segno usato per la terna, di
solito levogira, il che significa che a , b , a x b sono orientati
rispettivamente secondo il pollice, l’indice ed il medio della
mano destra (ovvero regola cavaturaccioli).
Ne discende che il prodotto vettoriale di due vettori paralleli è
nullo.
axb
b
a
Il prodotto vettoriale di due vettori viene fatto, di solito, mediante somma dei prodotti delle componenti.
In una rappresentazione cartesiana i prodotti vettoriali dei versori diversi tra di loro sono pari a ±1 a seconda
dell’ordine della permutazione 123 (i,j,k), quelli dei versori con se stessi sono ovviamente nulli:


ei • e j = ε ijk e k


ovvero:
+ 1 se [i, j, k ]
; ε ijk = − 1
se [i, j, k ]
è una permurtazione pari (123, 231, 312)
è una permutazione dispari (321,213,132)
0 se almeno due indici sono uguali
i∧i = 0





(A.10)
; i ∧ j = k ; i ∧ k = −j
j ∧ i = −k ;
j∧ j = 0 ;
j∧ k = i
(A.11)
k ∧ i = 0 ; k ∧ j = −i ; k ∧ k = 0
A.4
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
ne discende la comoda rappresentazione:
[
] [
]
= [a b ] i ∧ i + [a b ] i ∧ j + [a b ] i ∧ k + [a b ] j ∧ i +
+ [a b ] j ∧ j + [a b ] j ∧ k + [a b ] k ∧ i + [a b ] k ∧ j + [a b ] k ∧ k =
= [a b − a b ] i + [a b − a b ] j + [a b − a b ] k
a ∧ b = a x i + a y j + a z k ∧ bx i + b y j + bz k =
x
x
x
y
y
y
z
y
x
y
z
z
y
z
y
z
z
x
x
x
x
z
z
x
y
y
y
j
k
az
bz
z
(A.12)
z
x
Formalmente vale la notazione:
i
a ∧ b = ax
bx
ay
by
(A.13)
E’ facile rilevare che il prodotto vettoriale:
•
•
•
È non commutativo, i.e.
E’ distributivo, i.e.
Non è associativo, i.e.
a ∧ b = − b ∧ a (è alternante)
a ∧ [b + c] = a ∧ b + a ∧ c
a [b ∧ c] ≠ [a ∧ b]c
F
Un’applicazione semplificativa del prodotto vettoriale tipica della
meccanica è la determinazione del momento M di una forza F
→
P
M = r ∧ F ; r = PO
applicata in O rispetto ad un punto P:
O
r
Il prodotto tensoriale (o diadico) di due vettori è rappresentato dal semplice prodotto formale delle
loro rappresentazioni:
ab = a x i + a y j + a z k bx i + b y j + bz k =
[
][
[ ]
] j j + [a b ] jk + [a
[
]
]
] ki + [a
= [a x b x ] ii + a x b y i j + [a x b z ] i k + a y b x ji +
[
+ a y by
y
z
z
bx
z
]
(A.14)
b y k j + [a z b z ] k k
E’ ovviamente comoda la rappresentazione matriciale:
i
i a x b x

a b = j a y b x
k  a z b x
j
axby
a yby
azby
k
a x bz 

a ybz 
a z b z 
(A.15)
E’ facile rilevare che il prodotto diadico
•
•
È non commutativo, i.e.
E’ distributivo, i.e.
a b ≠ ba
a [b + c] = a b + a c
A.5
C.GOLIA – Fluidodinamica
A.3
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Prodotti di tre vettori
Doppio prodotto misto:
(a ∧ b ) • c = d =
ax
ay
az
bx
bz
bz
cx
cy
cz
(A.16)
c
b
a
d è pari al volume del parallelogramma rappresentato dai tre vettori.
Vale l’indentità (permutativa):
(a ∧ b ) • c = (c ∧ a ) • b = (b ∧ c ) • a
(A.17)
Doppio prodotto vettoriale
a ∧ (b ∧ c )
non commutativo
≠
(b ∧ c ) ∧ a
(A.18)
Valgono le indentità:
a ∧ (b ∧ c ) = b (a • c ) − c (a • b ) ;
a ∧ (b ∧ c ) + b ∧ (c ∧ a ) + c ∧ (a ∧ b ) = 0
(A.19)
Nota: dato un vettore a ed una direzione n, il vettore si può scomporre come somma di due vettori di cui uno
parallelo ad n ed un altro normale ad n, come segue:
parallelo ad n
normale ad n
a = (a • n ) n + n ∧ (a ∧ n )
A.4
(A.20)
Sistemi di riferimento
Anche se abbiamo dimostrato l’algebra vettoriale per un sistema di riferimento cartesiano, essa si applica
parimenti ad altri sistemi ortogonali, quali ad esempio il cilindrico e lo sferico.
Sistema polare piano (r,θ)
y
iθ
R = r i r (θ ) (vettore posizione)
ir
(A.21)
V = Vr i r + Vθ i θ (vettore velocità)
valgono le seguenti relazioni per il cambiamento di coordinate
(rispetto al cartesiano)
x = r cos θ

 y = r sin θ
i r = cos θ i + sin θ j

i θ = − sin θ i + cos θ j
r
j
θ
x
(A.22)
i
A.6
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
y
Sistema polare ellittico piano (ρ,θ)
Esempio di sistema non ortogonale
eρ
eθ
b
ρ
j
R = ρ eρ (θ) (vettore posizione)
θ
x
(A.23)
i
V = Vρ e ρ + Vθ e θ
valgono le seguenti relazioni per il cambiamento di coordinate
(rispetto al cartesiano)
x = a ρ cos θ

 y = b ρ sin θ
;
2
2

ρ =  x  +  y 

a  b


−1  a y 
θ = tan  b x 



; ρ ∈ (0, ∞ )
(A.24)
; θ ∈ [0, 2π]
y
Sistema cilindrico (r,θ.z)
R = r i r (θ) + z i z (vettore posizione)
V = Vr i r + Vθ i θ + Vz i z
a
ir
iθ
iz
x
θ
r
(A.25)
z
z
valgono le seguenti relazioni per il cambiamento di coordinate (rispetto al cartesiano)
x = r cos θ

 y = r sin θ
z = z

i r = cos θ i + sin θ j

i θ = − sin θ i + cos θ j

i z = k
z
Sistema sferico (r,θ,χ)
R = r ir
V = Vr i r + Vθ i θ + Vχ i χ
(A.26)
ir
iχ
θ
r
(A.27)
iq
y
valgono le seguenti relazioni per il cambiamento di coordinate x
(rispetto al cartesiano)
i r = sin θ cos χ i + sin θ sin χ j + cos θ k
x = r sin θ cos χ


 y = r sin θ sin χ
i θ = cos θ cos χ i + cos θ sin χ j − sin θ k
z = r cos θ


i χ = − sin χ i + cos χ j
χ
(A.28)
A.7
C.GOLIA – Fluidodinamica
A.5
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Differenziazione dei vettori
Data una rappresentazione di un vettore in un sistema ortonormale: a = a1 e1 + a 2 e 2 + a 3 e3 la derivata di a
rispetto ad una generica variabile “n” è data dal solito procedimento di derivazione:
∂
∂a
[a 1 e1 + a 2 e 2 + a 3 e 3 ] = ∂[a 1 e1 ] + ∂[a 2 e 2 ] + ∂[a 3 e 3 ] =
=
∂n
∂n
∂n
∂n ∂n
∂[e 3 ]
∂[e1 ] ∂[a 2 ]
∂[e 2 ] ∂[a 3 ]
∂[a 1 ]
=
+
e1 + a 1
e2 + a 2
e3 + a 3
+
∂n
∂n
∂n
∂n
∂n
∂n
Il problema è di determinare le derivate dei versori
Piano z=costante
coordinati rispetto alla variabile.
iθ(θ+dθ)
Ricordiamo che la derivata di un versore (vettore di
ir(θ+dθ)
modulo unitario) rappresenta la direzione verso cui il
versore si sposta rispetto alla variazione derivata
iθ(θ)
r
(rimane un versore).
ir(θ)
Per un sistema cartesiano, i versori coordinati sono
θ θ+dθ
costanti, essi non variano con il punto e quindi tutte le
rispettive derivate dei versori sono nulle.
Così non è per i sistemi non cartesiani.
Per le coordinate cilindriche vale:
∂i r
= 0;
∂r
∂i θ
=0;
∂r
∂i z
=0
∂r
∂i r
= iθ ;
∂θ
∂i r
=0 ;
∂z
∂i θ
= −i r ;
∂θ
∂i θ
=0;
∂z
∂i z
=0
∂θ
∂i z
=0
∂z
(A.29)
ir(θ+dθ)
ir(θ)
iθ(θ)
iθ(θ+dθ)
(A.30)
Per coordinate sferiche vale:
∂i r
=0 ;
∂r
∂i r
= iθ ;
∂θ
∂i r
= sinθ i χ ;
∂χ
∂i θ
=0;
∂r
∂i θ
= −i r ;
∂θ
∂i θ
= cos θ i χ ;
∂χ
∂i χ
∂r
∂i χ
∂θ
∂i χ
∂χ
=0
=0
(A.31)
= −sinθ i r . − cos θ i θ
χ=costante
Piano
ir(θ)
θ+dθ
iθ(θ) i (θ+dθ)
r
(θ
Cosθ iχ(χ)
sinθ ir(χ)
Iχ
χ+ dχ
iθ(θ+dθ)
A.8
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Esercizio A.1
Rappresentare analiticamente una forza di intensità 10N in direzione 30° dall’asse delle x in un campo piano
(x,y).
Esercizio A.2
Un’automobile percorre 3 km in direzione dell’asse y e successivamente 5 km a 45° rispetto agli assi x ed y.
Rappresentare graficamente ed analiticamente tali spostamenti.
EsercizioA.3
Dati i vettori (rappresentazione cartesiana):
a = 3xy i + 4zx j + yz k ;
b = z2 i + y2x j + xyz k ;
c = x2 i + y2 j +z2 k
ed il campo scalare
f = 3x2yz+3x+6
Determinare:
il modulo e la direzione dei vettori a, b, c , f a e gli angoli tra di loro, nel punto (1,2,3)
il vettore
a+b–c
nel punto (1,2,3)
il vettore
fa
nel punto (1,2,3)
il prodotto scalare
a•b
nel punto (1,2,3)
nel punto (1,2,3)
il prodotto vettoriale
a∧c
il doppio prodotto misto a • b ∧c
nel punto (1,2,3)
Esercizio A.4
Dati i vettori (rappresentazione cilindrica):
a = 3rz ir + 4z sinθ iθ+ z iz
;
b = 3 r cosθ ir + 4 r iθ+ z sinθ iz ; c = r ir + 2 iθ+ z r iz
ed il campo scalare
f = 3 r2 tanθ
Determinare:
il modulo e la direzione dei vettori a, b, c , f a e gli angoli tra di loro, nel punto (1, 30° ,6)
il vettore
fa
nel punto (1,30°,6)
il prodotto scalare
a•b
nel punto (1,30°,6)
nel punto (1,30°,6)
il prodotto vettoriale a ∧ c
il doppio prodotto misto
a • b ∧c
nel punto (1,30°,6)
A.6
Calcolo differenziale
dS
n
A.6.1 Operatore nabla
Il calcolo differenziale è’ regolato dall’operatore nabla (.) indicato come ∇(⋅)
oppure come
∂ (⋅)
; questo operatore ha un carattere sia vettoriale che differenziale.
∂r
V
E’ definito come (definizione integrale):
1
V →0 V
∇(⋅) = lim
∫∫ n(⋅) dS
(A.32)
S = ∂V
Quando l’operatore nabla opera su di un campo scalare “f”, ne discende il gradiente di f : denotato come
grad(f) ovvero ∇f.
A.9
C.GOLIA – Fluidodinamica
A.6.2
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Fattori di scala
Prima di ricavare le espressioni dell’operatore nabla, introduciamo il concetto dei fattori di scala, molto
utile per sistemi di coordinate non cartesiane.
Per un generico sistema (curvilineo ortogonale) ξ1, ξ2, ξ3, l’estensione dell’arco descritto dal vettore
posizione allorquando si ha una variazione infinitesima delle coordinate ξ1, ξ2, ξ3, è dato da:
ds 2 = ds12 + ds 22 + ds 32 = (h 1dξ1 ) + (h 2 dξ 2 ) + (h 3 dξ 3 )
2
2
2
(A.33)
Ovviamente se si suppone la variazione di una sola coordinata, le altre due rimanendo costanti, si ottiene:
h1 =
ds
dξ1
;
ξ 2 ,ξ3 costanti
h2 =
ds
dξ 2
ξ1 ,ξ3 costanti
h3 =
;
ds
dξ 3
ξ1 ,ξ1 costanti
(A.34)
Calcoliamo l’espressione del gradiente in questo sistema,
∇f = ∇1f + ∇ 2 f + ∇ 2 f = ∇1f e1 + ∇ 2 f e 2 + ∇ 3 f e 3
(A.35)
considerando separatamente le tre coordinate.
Applicando la definizione integrale rispetto alla sola coordinata ξ1 (vedi figura) risulta:
1
[f (ξ1 + dξ1 ) h 2 dξ 2 h 3dξ3 e1 − f (ξ1 ) h 2 dξ 2 h 3dξ 3 e1 ] =
V →0 h dξ h dξ h dξ
1
1 2
2 3
3
∇1f = ∇1f e1 = lim
= lim
dξ1
dξ1 →0
h1
se la funzione f è differenziabile il limite esiste ed è pari
alla derivata parziale, sicché:
1 ∂f
e1
h 1 ∂ξ1
Analogamente si ricavano:
∇ 1f =
∇ 2f =
(A.36)
[f (ξ1 + dξ1 ) − f (ξ1 ) ] e1
1 ∂f
e2
h 2 ∂ξ 2
∇ 3f =
(A.37)
dV=h1dξ1 h2dξ2 h3dξ3
dS=h2dξ2 h3dξ3
n=e1
n=−e1
1 ∂f
e3
h 3 ∂ξ 3
(A.38)
ξ1
ξ1
e1
ξ1+dξ1
sicché, in definitiva, l’espressione dell’operatore nabla, e
quindi del gradiente di un campo scalare “f” sono, per un qualsiasi sistema di coordinate ortonormali:
∇(⋅) =
1 ∂ (⋅)
1 ∂ (⋅)
1 ∂ (⋅)
e3
e2 +
e1 +
h 3 ∂ξ 3
h 2 ∂ξ 2
h 1 ∂ξ1
∇f =
1 ∂f
1 ∂f
1 ∂f
e1 +
e2 +
e3
h 1 ∂ξ1
h 2 ∂ξ 2
h 3 ∂ξ 3
Restano quindi da determinare i fattori di scala nei vari sistemi di riferimento.
Risulta agevole verificare che:
h x = 1

Cartesiano (x,y,z):
h y = 1

h z = 1
(A.39)
(A.40)
A.10
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Cilindrico (r,θ,z):
h r = 1

h θ = r
h = 1
 z
(A.41)
Sferico (r,θ,χ):
h r = 1

h θ = r
h = r sin θ
 χ
(A.42)
A.6.3 Gradiente
Ne derivano le espressioni del gradiente di f , ∇f:
Cartesiano(x,y,z):
∇f =
∂f
∂f
∂f
k
j+
i+
∂z
∂y
∂x
(A.43)
Cilindrico(r,θ,z):
∇f =
∂f
1 ∂f
∂f
iθ +
iz
ir +
∂r
r ∂θ
∂z
(A.44)
Sferico (r,θ,χ):
∇f =
∂f
1 ∂f
1 ∂f
ir +
iθ +
iχ
∂r
r ∂θ
r sin θ ∂χ
(A.45)
Nota: data una direzione n, la derivata di f nella direzione n è data da:
∂f
= n • ∇f
∂n
(A.46)
da questa si deduce che:
il gradiente di f, ∇f , è un vettore che ha per modulo la massima
variazione di f ed è diretto nella direzione di massima variazione che è
normale alle isosuperfici f=costante.
A.6.4
Divergenza di un campo vettoriale V
La definizione integrale è:
1
n • V dS
V →0 V
S=∂V
∇ • V = lim
∫∫
(A.47)
Per determinarne le espressioni, preferiamo usare il calcolo simbolico (vettoriale-differenziale) sfruttando le
relazioni trovate per i fattori di scala.
Ne deriva l’espressione differenziale generale nel sistema ξ1, ξ2, ξ3 ; V = V1 e1 + V2 e 2 + V3 e 3 :
∇•V =
1  ∂ (h 2 h 3 V1 ) ∂ (h 1 h 3 V2 ) ∂ (h 1 h 2 V3 ) 
+
+


h 1 h 2 h 3  ∂ξ1
∂ξ 2
∂ξ 3

(A.48)
Ne derivano le espressioni della div( V) , ∇•V :
A.11
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Cartesiano(x,y,z):
∇•V =
∂u ∂v ∂w
+
+
∂x ∂y ∂z
(A.49)
Cilindrico(r,θ,z):
∇•V =
1 ∂ (rVr ) 1 ∂Vθ ∂Vz
+
+
r ∂r
r ∂θ
∂z
(A.50)
∇•V =
Sferico (r,θ,χ):
(
)
1 ∂ (Vθ sin θ )
1 ∂Vχ
1 ∂ r 2 Vr
+
+
2
∂r
∂θ
r sin θ
r sin θ ∂χ
r
(A.51)
A.6.5 Significato fisico della divergenza del campo di velocità
Consideriamo la definizione integrale:
1
n • V dS
V →0 V
S= ∂V
∇ • V = lim
∫∫
(A.52)
Notiamo che:
L3 L
= ] nella direzione n
L2 t t
n•V
è il flusso di volume [analisi dimensionale:
∫∫ n • V dS
è la portata di volume attraverso la superficie S che avvolge il volume V di
S = ∂V
una particella
Per cui:
∇ • V = lim
V →0
1
n • V dS
V S=∂V
∫∫
(A.53)
La divergenza della velocità rappresenta:
• la portata di volume per unità di volume di una particella fluida , i.e. la variazione di volume per unità
di volume
• ergo se ∇ • V = 0 il volume elementare della particella non cambia, ergo la densità rimane costante, ergo
il campo di moto è incompressibile
A.6.6
Rotore di un campo vettoriale V
Le definizioni integrali sono varie:
dal teorema di Gauss generalizzato:
1
n ∧ V dS
V →0 V
S=∂V
∇ ∧ V = lim
∫∫
(A.54)
Per determinarne le espressioni dell’operatore prodotto vettoriale, preferiamo usare il calcolo simbolico
(vettoriale-differenziale) sfruttando le relazioni trovate per i fattori di scala.
Ne deriva l’espressione differenziale generale nel sistema ξ1, ξ2, ξ3 ; V = V1 e1 + V2 e 2 + V3 e 3 :
A.12
C.GOLIA – Fluidodinamica
∇∧V =
Appendice A - Richiami di Calcolo vettoriale e tensoriale
1  ∂(h 2 V2 ) ∂(h1V1 ) 
1  ∂(h 3 V3 ) ∂(h 2 V2 ) 
1  ∂(h1V1 ) ∂(h 3 V3 ) 
−
−
−
 e2 +

 e1 +

 e3 (A.55)

h1h 2  ∂ξ1
h 2 h 3  ∂ξ 2
h1h 3  ∂ξ3
∂ξ 2 
∂ξ1 
∂ξ3 
Ne derivano le espressioni: rot( V) , ∇∧V:
Cartesiano(x,y,z):
 ∂v ∂u 
 ∂w ∂v 
 ∂u ∂w 
j+  −  k
− i+ −
∇∧V = 

 ∂z ∂x 
 ∂x ∂y 
 ∂y ∂z 
(A.56)
Cilindrico(r,θ,z):
1  ∂ (rVθ ) ∂ (Vr ) 
1  ∂ (Vz ) ∂ (rVθ ) 
 ∂ (Vr ) ∂ (Vz ) 
eθ + 
er + 
ez
−
−
−
∇∧V = 


r  ∂r
r  ∂θ
∂θ 
∂r 
∂z 
 ∂z
Sferico (r,θ,χ):
∇∧V =
1  ∂(r sin θ Vχ ) ∂(rVθ ) 
1  ∂(Vr ) ∂(r sin θ Vχ )
1  ∂(rVθ ) ∂(Vr ) 
eχ
−
−
−

 er +

 eθ + 
r sin θ  ∂χ
r  ∂r
∂θ
∂χ 
∂r
∂θ 
r sin θ 

2
(A.57)
(A.58)
Altra definizione integrale della componente del rotore di V nella direzione n, deriva dal teorema di Stokes:
∫∫ (∇ ∧ V ) • n dS = ∫
S
V • dc
⇒
C = ∂S


V • dc
 S C=∂S

1
(∇ ∧ V ) • n = lim

S→0
∫
(A.59)
A.6.6.1 Significato fisico del rotore:
In coordinate cilindriche calcoliamo il rotore di un campo di moto rigido dotato di una velocità di rotazione
Ω ez
Sarà ovviamente Vr=0, Vθ=Ω r, Vz=0 da cui:
(∇ ∧ V )r = 0 , (∇ ∧ V )θ = 0 ,
(∇ ∧ V )z
= 2Ω
(A.60)
Ne discende , in generale, che il modulo del rotore della velocità corrisponde al doppio della velocità
angolare della particella e la sua direzione è normale al piano del moto, con il verso coerente con la terna
(regola cavaturacciolo)
Esercizio A.5
Dati vettori:
a = 3xy i + 4zx j + yz k
ed il campo scalare
Determinare:
il gradiente di f
la divergenza di a
il rotore di b
;
b = z2 i + y2x j + xyz k ;
f = 3x2yz+3x+6
la sua direzione ed il suo modulo nel punto (1,2,3)
∇f
∇ • a nel punto (1,2,3)
∇ ∧ b la sua direzione ed il suo modulo
nel punto (1,2,3)
Esercizio A.6
Dati i vettori (rappresentazione cilindrica):
a = 3rz ir + 4z sinθ iθ+ z iz
;
b = 3 r cosθ ir + 4 r iθ+ z sinθ iz
A.13
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
f = 3 r2 tanθ
ed il campo scalare
Determinare:
il gradiente di f
la divergenza di a
il rotore di b
∇f
la sua direzione ed il suo modulo nel punto (1,30°,60°)
∇ • a nel punto (1,2,3)
∇ ∧ b la sua direzione ed il suo modulo nel punto (1,2,3)
Esercizio A.7
Dati i campi vettoriali:
1. V(r,θ,χ)
= (k/r2) ir
(in uno spazio 3D, coordinate cilindriche/sferiche)
2. V(r,θ)
=(k/R) ir
(in uno spazio 2D, coordinate polari/cilindriche)
3. V(r,θ,χ)
= (k/r2) iθ
(in uno spazio 3D, coordinate cilindriche/sferiche)
4. V(r,θ,χ)
= (k/R) iθ
(in uno spazio 2D, coordinate polari/cilindriche)
5. V(x,y)
= k
6. V(x,y)
7. V(r,θ)
8. V(x,y)

y
x
i+
2
+
x
+
y2
x
y
2
 2
(

) (
)

j

(in uno spazio 2D, coordinate cartesiane)

x
y
j
i+
2
2 
x2 + y 
 x2 + y
sinθ
cos θ
= k  2 i r + 2 i θ 
R

 R
= k −

= k −

(
) (
x 2 − y2
(x
2
+y
)
2 2
i+
)
(x
2xy
2
+y
)
2 2
(in uno spazio 2D, coordinate cartesiane)
(in uno spazio 2D, coordinate cilindriche)

j (in uno spazio 2D, coordinate cartesiane)

Determinare:
le divergenze ed i rotori dei campi vettoriali nei rispettivi spazi coordinati
A.7
Operatori differenziali del secondo ordine
A.7.1 Laplaciano
La definizione integrale è:
1
1
∂ (.)
n • ∇(.) dS = lim
dS
V →0 V
V →0 V
∂n
S = ∂V
S = ∂V
∇ 2 (⋅) = ∇ • ∇(.) = lim
∫∫
∫∫
(A.61)
Per determinarne le espressioni, preferiamo usare il calcolo simbolico (vettoriale-differenziale) sfruttando le
relazioni trovate per i fattori di scala.
∇ 2f =
1
h 1h 2 h 3
 ∂  h 2 h 3 ∂f 
∂  h 1 h 3 ∂f 
∂  h 1 h 2 ∂f  




+

+
 ∂ξ1  h 1 ∂ξ1  ∂ξ 2  h 2 ∂ξ 2  ∂ξ 3  h 3 ∂ξ 3  
(A.62)
Ne derivano le espressioni del laplaciano di f: ∇2 f
A.14
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Cartesiano(x,y,z):
∇ 2f =
∂ 2f ∂ 2f ∂ 2f
+
+
∂x 2 ∂y 2 ∂z 2
∇ 2f =
1 ∂  ∂f  1 ∂ 2 f ∂ 2 f
+
r  +
r ∂r  ∂r  r 2 ∂θ 2 ∂z 2
(A.63)
Cilindrico(r,θ,z):
(A.64)
Sferico (r,θ,χ):
∇ 2f =
1 ∂  2 ∂f 
1
1
∂ 2f
∂ 
∂f 
r
sin
+
+
θ




∂θ  r 2 sin 2 θ ∂χ 2
r 2 ∂r  ∂r  r 2 sin θ ∂θ 
(A.65)
Esercizio A.8
Date le funzioni:
f(x,y,z) = x 2 + y 2 + z 2 (distanza dall’origine in uno spazio 3D, coordinate cartesiane)
1. f(r,θ,χ) = r
2. f(x,y) =
(distanza dall’origine in uno spazio 3D, coordinate sferiche)
x 2 + y2
(distanza dall’origine in uno spazio 2D, coordinate cartesiane)
3. f(R,θ) = R
4. f=Ln(R)
5.
6.
7.
8.
9.
(distanza dall’origine in uno spazio 2D, coordinate cilindriche)
2
= ln x + y 2
(in uno spazio 3D, coordinate cartesiane)
f=Ln(r) = ln x 2 + y 2 + z 2
2
2)
(funzione in uno spazio 2D, coordinate cartesiane)
F(x,y) =k( x - y
F(x,y) = k(xy)
(funzione in uno spazio 2D, coordinate cartesiane)
F(x,y,z)
=k(xyz)
(funzione in uno spazio 3D, coordinate cartesiane)
F(r,θ) =k θ
(funzione in uno spazio 2D, coordinate cilindriche)
y
10. F(x,y) =k tan −1  
x
11.
12.
13.
14.
(in uno spazio 2D, coordinate cartesiane)
(funzione in uno spazio 2D, coordinate cartesiane)
F(R,θ) =Rα sin(αθ)
(funzione in uno spazio 2D, coordinate cilindriche, α è un numero)
F(R,θ) =Rα cos(αθ) (funzione in uno spazio 2D, coordinate cilindriche, α è un numero)
f=1/R
(R=distanza dall’origine in uno spazio 2D, coordinate cartesiane)
r=1/r
(r=distanza dall’origine in uno spazio 23, coordinate cartesiane o sferiche)
Determinare:
i gradienti ed i laplaciani delle funzioni nei rispettivi spazi coordinati
Esercizio: A.9
Verificare le identità
∇ 2 A = ∇(∇ • A ) − ∇ ∧ (∇ ∧ A )
a)
∇ • (∇ ∧ A ) = 0
b)
c)
∇ ∧ (∇f ) = 0
d)
e)
(V • ∇ )V = 12 ∇(V • V ) − V ∧ (∇ ∧ V )
∇ ∧ [(∇ ∧ V ) ∧ V ] = −V(∇ • (∇ ∧ V )) + (V • ∇ )(∇ ∧ V ) − [(∇ ∧ V ) • ∇ ]V + (∇ ∧ V )(∇ • V )
A.15
C.GOLIA – Fluidodinamica
A.8
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Algebra tensoriale
Considereremo nel seguito soltanto rappresentazioni cartesiane.
La rappresentazione algebrica del generico tensore A è:
A = i A xx i + i A xy j + i A xz k +
+ j A yx i + j A yy i + j A yz i +
(A.66)
+ k A zx i + k A zy i + k A zz i
La rappresentazione matriciale del generico tensore A è:
A xx
j k A yx
A zx
A= i
A xy
A yy
A zy
A xz
A yz
A zz
i
j
k
(A.67)
Di solito si considera implicitamente il prodotto con i vettori contenenti i versori coordinati, per cui si
conviene rappresentare il tensore A semplicemente con la sua matrice delle componenti scalari Aij:
A xx
A → A yx
A zx
A xy
A yy
A zy
A xz
A yz
A zz
(A.68)
Il trasporto At del tensore è rappresentato dalla matrice trasposta, i.e. quella che si ricava sostituendo le righe
con le colonne:
A xx A yx A zx
t
A → A xy A yy A zy
(A.69)
A xz A yz A zz
( )
Ovviamente A t
t
=A
t
Un tensore si dice simmetrico se coincide con il suo trasposto, A = A , i.e. Aij=Aji ;
1 2 3
esempio: 2 4 5
3 5 6
ovviamente un tensore trasposto è definito da solo 6 componenti scalari.
Un tensore si dice anti-simmetrico se .
Aij=-Aji ;
0
1 2
es. − 1 0 3
−2 −3 0
(A.70)
ovviamente un tensore trasposto è definito da solo 3 componenti scalari ( nota: le componenti diagonali di un
tensore anti-simmetrico devono essere nulle).
Il tensore unitario è U definito come:
1 0 0
U= 0 1 0
0 0 1
(A.71)
A.16
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
La traccia di un tensore Tr(A) è lo scalare somma delle componenti sulla diagonale principale:
Tr(A)=Axx+Ayy+Azz.
La traccia del tensore unitario è pari a 3 ed è nulla per un tensore antisimmetrico. La traccia di un tensore
diadico a b è pari al prodotto scalare delle componenti (sinistra e destra) Tr(a b) = a•b
Ogni tensore può essere espresso come somma di un parte simmetrica e di una anti-simmetrica: A= A s+ A a:
A=
A xx
A → A yx
A zx
=
1
2
1
2
A xy
A yy
A zy
A xx
A yx + A xy
(
A xz
A yz =
A zz
1
2
)
(A xz + A xz )
1
2
(A
(A
xy
+ A yx
A yy
zy
+ A yz
1
2
[A + A ]+ [A − A ]
t
) (A + A )
(A + A ) + (A
(A
)
A
1
2
1
2
xz
zx
yz
zy
zz
t
1
2
1
2
1
2
0
yx − A xy
xz
(A.72)
)
− A xz )
1
2
1
2
(A
(A
xy
− A yx
0
zy
− A yz
) (A
(A
)
1
2
1
2
xz
yz
− A zx )
− A zy
(A.73)
)
0
Si definisce vettore di un tensore A , il vettore Av = εijk Aij ek.
Esso è nullo per un tensore simmetrico e, per un tensore diadico ab è pari al prodotto vettoriale delle
componenti (sinistra e destra) (a b)v = a^b
A.8.1
Prodotto scalare tra un vettore n ed un tensore A
E’ un vettore (nota il prodotto scalare abbassa di due unità la somma degli ordini tensoriali dei fattori)
Prodotto scalare da destra:
A•n
(A.74)
Espressione algebrica:
i A xx i + i A xy j + i A xz k + j A yx i + j A yy j + j A yz k + 
A•n = 
 • nx i + ny j+ nz k =
+ k A zx i + k A zy j + k A zz k

[
svolgendo l'algebra
=
[
+ i [A
[
]
(A.75)
i A xx n x + A xy n x + A xz n x +
]
]
]
+ j A yx n x + A yy n x + A yz n x +
zx
n x + A zy n x + A zz n x
Espressione matriciale:
A xx
A xy
A xz n x
A • n → A yx
A yy
A yz n y
A zx
A zy
A zz n z
(A.76)
Prodotto scalare da sinistra:
n•A
(A.77)
Espressione algebrica:
A.17
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
i A xx i + i A xy j + i A xz k + j A yx i +
n • A = nx i + ny j+ nz k • 
+ j A yy j + j A yz k + k A zx i + k A zy j + k A zz
[
svolgendo l'algebra
[
=
]
[A
xx

=
k 
]
(A.78)
n x + A yx n x + A zx n x i +
]
+ A xy n x + A yy n x + A zy n x j +
[
]
+ i A xz n x + A zy n x + A zz n x k
Espressione matriciale:
n • A → nx
ny
A xx
A xy
A xz
n z A yx
A yy
A yz
A zx
A zy
A zz
(A.79)
Nota:
• i due prodotti sono in genere diversi a meno che il tensore non sia simmetrico.
n • A = At • n ;
A • n = n • At ;
n•U = U•n = n
• Vale infatti
•
•
Sfruttando la definizione di parte antisimmetrica di un tensore, Aa si ottiene V•A = A•V+Av ∧V
∇ ∧ Av = -2 V•Aa
Valgono le seguenti identità
Av ∧V = 2 V•Aa
A.8.2 Doppio prodotto scalare tra tensori
Vale:
A:B= Aij Bji
NOTA: in alcuni testi si definisce A:B= Aij Bij
Nota: il doppio prodotto scalare tra diadi non è associativo, i.e.
a b : cd = [a • d ] [b • c] ≠ [a • b] [c • d ]
A.8.3 Analisi spettrale di tensori
Il prodotto scalare da destra di un tensore T con un vettore a è, in genere, un vettore b :
T•a = b
(A.80)
Poniamoci il problema di esaminare cosa accade se imponiamo che il vettore b sia parallelo ad a : che sia
cioè b = λ a [nota: λ è uno scalare, e il modulo di a varia se λ ≠ ± 1] dovrà ovviamente essere per la (A.80):
T•a = λ a
(A.81)
ovvero:
[ T − λ U ]• a = 0
ovvero:
Tik a k = λ a i
ovvero (Tik − λδ ik ) a k = 0
(A.82)
Ovviamente le (A.81) e (A.82) soddisfano la soluzione banale: a = 0 .
L’ analisi spettrale dei tensori analizza se esistono soluzioni non banali per le (A.82), in tal caso:
A.18
C.GOLIA – Fluidodinamica
•
•
Appendice A - Richiami di Calcolo vettoriale e tensoriale
i vettori a sono chiamati autovettori (ovvero vettori caratteristici ovvero eigenvectors) di T e i loro
versori definiscono le direzioni principali del tensore,
gli scalari λ sono chiamati autovalori (ovvero valori caratteristici ovvero eigenvalues) e
rappresentano le componenti del tensore T lungo le direzioni principali.
Preferiamo considerare il problema di ridurre il generico
tensore T ai suoi assi principali, procedendo con un esempio
molto semplice:
Y
Y’
Consideriamo un sistema di 3 masse m1, m2, m3 poste in un
piano x, y , di cui vogliamo analizzare il tensore d’inerzia:
I
I =  11
I 21
I12 
I 22 
m2
2
m3
1
m1
X’
ϕ
(A.83)
2
1
-1
siano:
X
m1 = 1 ; m 2 = 2 ; m 3 = 3
(A.84)
I11 =
3
∑
( )
mj yj
2
= 12
I12 = I 21 =
j=1
3
∑
(
)
m j x jy j = 9
I 22 =
j=1
3
∑
( )
mj xj
2
= 15
j=1
La soluzione non banale delle (A.82)
I11a x + I1 2 a y = λ a x
I 22 a x + I 2 2 a y = λ a y
richiede la soluzione del sistema di equazioni:
(I
11
)
− λ a x + I1 2 a y = 0
(
)
I 22 a x + I 2 2 − λ a y = 0
(A.85)
(A.86)
che ha soluzione no nulla solo se il determinante della matrice è nullo:
I11 − λ
I1 2
I 21
I22 − λ
=0
(A.87)
ovvero se è soddisfatta l' equazione caratteristica:
λ2 − (I11 + I 22 ) λ + (I11I 22 − I12 I 21 ) = 0
(A.88)
che ha le radici:
λ1 =
I11 + I 22 1
+
2
2
per il caso analizzato:
(I11 − I 22 )2 + I12 I 21
λ1=22.62
λ2 =
I11 + I 22 1
−
2
2
(I11 − I 22 )2 + I12 I 21
(A.89)
λ2= 4.376
Nota se I12=I21=0 risulta λ1 = I11 e λ2 = I22 e quindi il vettore a non è ruotato (gli assi x e y sono principali
d’inerzia).
2
In genere se I12 ≠0 e I21≠0 e (I11 − I 22 ) + I12 I 21 > 0 si hanno due soluzioni reali cui corrispondono due
vettori caratteristici
a(1) ed a(2) che sono indeterminati essendo la (A.82) e quindi la (A.85) un sistema
omogeneo.
A.19
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Questi vettori sono quindi individuati a meno di una costante (di solito si impone arbitrariamente una
componente e successivamente si normalizza il vettore ponendone il modulo unitario): ad esempio dalla
(A.85)
I11 a x + I1 2 a y = λ a x
(A.90)
I 21 a x + I 2 2 a y = λ a y
ponendo ay=1 si ricavano le due forme equivalenti:
I11a x − λ a x = − I1 2 a y
Ne segue che gli autovettori
I12
λ − I11
→ ax =
,
ay =1
(A.91)
λ − I 22
I 21 a x = λ a y − I 2 2 a y → a x =
,
ay =1
I 21
a(1) ed a(2)
corrispondenti ai due autovalori λ1 ed λ2 sono:
a (1) x =
a
( 2)
x
I12
λ1 − I11
a (1) y = 1
,
(A.92)
I12
=
λ 2 − I11
,
a
( 2)
y
=1
di modulo:
a
(1)
=
a ( 2) =
(I12 )2 + (λ1 − I11 )2
λ1 − I11
(A.93
(I12 )2 + (λ 2 − I11 )2
λ 2 − I11
I due autovettori, normalizzati, diventano:
a
per il caso analizzato:
(1)


=



I12
(λ1 − I11 ) + (I12 )
(λ1 − I11 )
(λ1 − I11 )2 + (I12 )2
2
2






a
(2)


=



1) –0.646374 i + 0.76302 j
I12
(λ 2 − I11 ) + (I12 )
(λ 2 − I11 )
(λ 2 − I11 )2 + (I12 )2
2
2)
2






(A.94
0.76302 i + 64637 j
E’ interessante fare il prodotto scalare di questi due autovettori:
a
=
(1)
•a
(2)
=
I12
I12
(λ1 − I11 )2 + (I12 )2 (λ 2 − I11 )2 + (I12 )2
(I12 )2 + (λ1 − I11 )(λ 2 − I11 )
(λ1 − I11 )2 + (I12 )2 (λ 2 − I11 )2 + (I12 )2
+
(λ1 − I11 )
(λ 2 − I11 )
(λ1 − I11 )2 + (I12 )2 (λ 2 − I11 )2 + (I12 )2
=
(A.95
Sostituendo in questa relazione i risultati della (A.89) ne risulta:
a
(1)
•a
(2)
=0
(A.96)
Ovvero gli autovettori sono tra di loro ortogonali
A.20
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Questi vettori individuano le due direzioni principali del tensore d’inerzia I, che hanno, rispetto all’asse x,
una inclinazione ϕ di:
a (y2 ) λ − I
a (y1) λ − I
tan ϕ2 = ( 2 ) = 2 11
(A.97)
tan ϕ1 = (1) = 1 11
I12
I12
ax
ax
φ1 = -49,7314°
per il caso analizzato:
φ2 = 40.2686
sostituendo le espressioni degli autovalori (A.89) nelle (A.97) si ritrova che ϕ2 = ϕ1 + π/2 ovvero si conferma
che le direzioni principali sono ortogonali l’una all’altra.
Se gli autovettori sono reali e distintiti, formano, se normalizzati, una matrice di rotazione:
[
R= a
(1)
a
( 2)
]
a (x1)
=  (1)
a y
a (x2 ) 

a (y2 ) 
la cui inversa è R
−1
=R
trasp
 a (x1)
=  ( 2)
a x
a (y1) 

a (y2 ) 
(A.98)
L’applicazione di questa rotazione alla matrice originaria la trasforma in una matrice diagonale:
R
−1
a (x1)
I R =  (1)
a y
a (x2 )   I11

a (y2 )  I 21
I12  a (x1)

I 22  a (y1)
a (x2 )  I'11
=
a (y2 )   0
0  λ1 0 
=
I'22   0 λ 2 
(A.99)
è invariato
(A.100)
Nota:
I’11 + I’22 ≅ 22.6241 +4.3759 = 27 = 15+12 = I11 + I22
L’estensione al caso 3D di un generico tensore T è immediata.
Il tensore è rappresentato dalla matrice:
 T11
T = T21
T31
T13 
T23 
T33 
T12
T22
T32
(A.101)
L’equazione degli autovalori è:
T12
T13 
T11 − λ

T − λ U = 0 = det  T21
T22 − λ
T23  = 0
 T31
T32
T33 − λ 
(A.102)
L’equazione caratteristica si ricava svolgendo il determinante della (A.98):
T
λ − λ (T11 + T22 + T33 ) + λ  22
 T32
3
2
T23
T33
+
T33
T31
T13
T11
+
T11
T21
T11 T12
T12 
 − T21 T22
T22 
T31 T32
T13
T23 = 0
(A.103)
T33
L’equazione caratteristica deve essere invariante: quindi i suoi coefficienti rappresentano gli invarianti del
tensore:
Inv1 = (T11 + T22 + T33 )
(A.104)
T
Inv 2 =  22
 T32
T23
T33
+
T11
T13
T31
T33
+
T11
T21
T12 

T22 
(A.105)
A.21
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
T11
T12
T13
Inv 3 = T21
T22
T23
T31
T32
T33
(A.106)
Nota: i tensori che hanno il primo invariante nullo: Inv1 = (T11 + T22 + T33 ) = Tr (T ) =0 sono detti deviatorici.
I tensori che hanno le componenti scalari invarianti rispetto ad arbitrarie rotazioni di assi sono detti isotropi.
Tutti i tensori di ordine zero (scalari) sono isotropi.
Nessun tensore di ordine uno (vettore) è isotropo.
La forma più generale di tensore isotropo di ordine due è il tensore unitario U ovvero
il simbolo di Kronecker: δij
Tutti i tensori isotropi di ordine maggiore di due si possono esprime come combinazioni del tensore δij
La forma più generale di tensore isotropo di ordine tre è rappresentato dal tensore di Ricci:
εiik =(ei ∧ ej) • ek
La forma più generale di tensore isotropo di ordine quattro è rappresentato dalla forma (A,B,C costanti
scalari):
ηiklm = A δik δlm+ B δil δkm+ C δim δkl
Ovviamente ogni tensore può essere scritto come somma di un tensore deviatorico ed uno isotropo:
1
1

 1
Tik = Tik − Tmm δ ik  + Tmm δ ik = D ik + Tmm δ ik
{
3424
14432443 3
1
3
deviatorico
Dik
Tr (T )
Tr (T )
T=T−
U+
U=
Tr (U )
Tr (U )
14243
D
A.9
(A.107)
isotropo
+
D
{
Tr (T )
U
1
4324
3
(A.108)
isotropo
deviatorico
Tensori di interesse in Fluidodinamica
tn
n
A.9.1 Tensore degli sforzi
Il tensore degli sforzi τ è definito come una entità fisica tale che :
tn = n • τ
tn =
Dove la tensione
dS
(A.109)
d F s  Forza 
dS  Superfice 
è lo sforzo viscoso dFs agente sull’areola dS di normale n.
Significato fisico della divergenza del tensore degli sforzi
Dalla definizione integrale risulta:
1
V →0 V
∇ • τ = lim
1
∫∫ n • τ dS = lim V ∫∫ t
S = ∂V
V →0
S = ∂V
n
1
V →0 V
dS = lim
∫∫
S = ∂V
d Fn
F
dS ≈ lim n
V →0 V
dS
(A.110)
A.22
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
ergo la ∇ • τ rappresenta il risultante degli sforzi superficiali viscosi, agente su di una particella fluida, per
unità di volume.
Calcolo della ∇ • τ (coordinate cartesiane)
Espressione algebrica:
∂
∂
∂
j+
∇•A =  i+
∂y
∂z
 ∂x
svolgendo l'algebra
=
 i A xx i + i A xy j + i A xz k + j A yx i +
k • 
 + j A yy j + j A yz k + k A zx i + k A zy j + k A zz

=
k 
 ∂A xz ∂A yz ∂A zz 
 ∂A xx ∂A xy ∂A xz   ∂A xy ∂A yy ∂A zy 
+
+
+
+
+
+
k
 j+ 
i+

∂y
∂z 
∂z 
∂y
∂y
∂z   ∂x
 ∂x
 ∂x
(A.111)
Espressione matriciale:
∂
∇•A →
∂x
Nota l’identità:
A xx
∂
A yx
∂z
A zx
∂
∂y
A xy
A xz
A yy
A yz
A zy
A zz
( )
∇ • p U = p∇ • U + U • ∇p = ∇p
A.9.2
(A.112)
(A.113)
Gradiente della velocità
Il Tensore diadico ∇ V entra nell’analisi della velocità di deformazione di una particella fluida.
Espressione algebrica:
[
 ∂
∂
∂ 
∇ V = i
+j +k
u i + v j+ u k
∂y
∂z 
 ∂x
∂v
∂w 
 ∂u
i  i+
j+
k +
∂x
∂x 
 ∂x
]
svolgendo l'algebra
=
 ∂u
∂v
∂w 
j i+
j+
k + k
∂y
∂y 
 ∂y
∂v
∂w 
 ∂u
 ∂z i + ∂z j + ∂z k 


(A.114)
Espressione matriciale:
∂
∂x
∂
∇V→
u
∂y
∂
∂z
∂u
∂x
∂u
v w →
∂y
∂u
∂z
∂v
∂x
∂v
∂y
∂v
∂z
∂w
∂x
∂w
∂y
∂w
∂z
(A.115)
E’ interessante calcolare le parti simmetriche ed antisimmetriche del Tensore diadico ∇ V
A.23
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
∇ V = [∇ V ] + [∇ V ] ≡ S + Ω =
s
a
(A.116)
∂u
∂x
 ∂u ∂v 
= 12  + 
 ∂y ∂x 
∂w 
1  ∂u
+

2
 ∂z ∂x 
 ∂v ∂u 
 + 
 ∂x ∂y 
∂v
∂y

v
∂w 
∂
1
 +

2
 ∂z ∂y 
1
2
∂u 
 ∂w ∂u 
1  ∂v
 − 
0
+ 

2
 ∂x ∂z 
 ∂x ∂y 
 ∂v ∂u 
∂v 
1  ∂w

0
+  + − 12  − 
2
 ∂x ∂y 
 ∂y ∂z 
 ∂w ∂v 
∂w
 ∂w ∂u 
+ 
−  − 12 
− 12 
∂z
 ∂x ∂z 
 ∂y ∂z 
1
2
 ∂w ∂u 
− 

 ∂x ∂z 
∂v 
1  ∂w

− 
2
 ∂y ∂z 
1
2
0
NOTA CHE:
la traccia di S (che coincide con la traccia di ∇ V ) è pari alla divergenza della Velocità : Tr(S)=∇•V
il vettore della parte antisimmetrica cioè di Ω (che coincide con il vettore di ∇ V ) è pari a Ωv=∇∧V
che Ω è esprimibile in funzione delle tre componenti del rotore della velocità detto vorticità ω:
 ∂w ∂v   ∂u ∂w 
 ∂v ∂u 
ω = ∇ ∧ V = 
−  i +  −
 j +  −  k = ω x i + ω y j + ω z k
 ∂y ∂z   ∂z ∂x 
 ∂x ∂y 
1
2
0
 ∂v ∂u 
 − 
 ∂x ∂y 
 ∂w ∂u 
− 

 ∂x ∂z 
0
∂v 
1  ∂w
1

−  = − 2 ωz
2
 ∂y ∂z 
1
ω
2 y
0
1
2
 ∂v ∂u 
0
Ω → − 12  − 
 ∂x ∂y 
 ∂w ∂v 
 ∂w ∂u 
+ 
−  − 12 
− 12 
x
∂
z
∂


 ∂y ∂z 
ωz
0
1
− 2 ωx
1
2
− 12 ωy
1
ω =
2 x
0
1
2
0
− ωz
ωy
ωz
0
− ωx
(A.117)
− ωy
ωx
0
(A.118)
Il vettore V • ∇ V rappresenta l’accelerazione convettiva di una particella fluida.
Per la sua determinazione si può considerarlo in due modi:
Come prodotto a sinistra della velocità con la diade ∇V: V • (∇V ) in tal caso risulta
Espressione algebrica:
  ∂u

∂v
∂w 
i  ∂x i + ∂x j + ∂x k  +


 

V • [∇ V ] = u i + v j + w k • 
=
+ j  ∂u i + ∂v j + ∂w k  + k  ∂u i + ∂v j + ∂w k  
 ∂z
  ∂y
∂z  
∂z
∂y 
∂y


[
]
(A.119)
 ∂u
∂w
∂w 
∂v
∂w   ∂w
∂u
∂u   ∂v
j + u
k
+v
+w
+v +w
= u
+ v + w  i + u

∂y
∂x 
∂y
∂z   ∂x
∂y
∂z   ∂x
 ∂x
Espressione matriciale:
V • [∇ V ] → [u
∂u
∂x
∂u
v w]
∂y
∂u
∂z
∂v
∂x
∂v
∂y
∂v
∂z
∂w
∂x
∂w
∂y
∂w
∂z
(A.120)
A.24
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Come prodotto dell’ operatore scalare (V • ∇ )(.) sulla velocità V:
(V • ∇ )V
(A.121)
Espressione algebrica:

[V • ∇]V =  [u i + v j + w k ] •  ∂
 ∂x

 ∂
∂
+v +w
= u
∂y
 ∂x
 ∂u
∂u
+v +w
= u
∂y
 ∂x
i+
[
∂
∂ 
j + k   ui + v j + w k =
∂y
∂z  
[
]
]
∂
ui + v j + w k =
∂z 
(A.122)
 ∂w
∂w 
∂w
∂w 
∂v
∂u   ∂v
k
j + u
i + u
+w
+v
+v +w


∂x 
∂y
∂z 
∂y
∂z   ∂x
 ∂x
Espressione matriciale:

∂ 


∂x  u

[ V • ∇]V → [u v w ] ∂  v
∂y

∂  w

∂y 

Esercizio.A.10
Verifica l’identità vettoriale:
∇•S =
1
2
(A.123)
[∇ V + ∇(∇ • V)]
2
Esercizio.A.11
Verifica l’identità vettoriale:
 V2 
 + (∇ ∧ V ) ∧ V
V • ∇V = ∇

 2 
Esercizio.A.12
Verifica l’identità vettoriale:
 V2 
 + 2V• Ω
V • ∇V = ∇

 2 
Esercizio.A.13
Determina le componenti di
n•τ•V
(rappresenta la potenza dissipata dallo sforzo viscoso agente su di una superficie)
Esercizio.A.14
Verifica l’identità
(∇ • τ)• V = (∇ • τ)
•V+τ
trasp
: (∇ V )
(rappresenta la potenza dissipata dal risultante degli sforzi viscosi agente sulla superficie di una particella,
per unità di volume)
Esercizio.A.15
Verifica le seguenti identità
∇(a • b ) = (∇a ) • b + (∇ b ) • a
∇(a ∧ b ) = b • (∇ ∧a ) − a • (∇ ∧ b )
A.25
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
∇ ∧ (a ∧ b ) = a (∇ • b ) − b(∇ • b ) − a • (∇ b ) + b • (∇ a )
∇(a ∧ b ) = (∇a ) ∧ b + (∇ b ) ∧ a
∇ • (a b ) = (∇ • a )b + a • (∇ b )
∇ ∧ (a b ) = (∇ ∧ a )b − a ∧ (∇ b )
A.10
Elementi di calcolo integrale
Considerata la figura a lato, valgono i seguenti teoremi di Gauss:
del gradiente:
∫∫∫ ∇f dV = ∫∫ n f dS
n
(A.124)
S = ∂V
V
S
della divergenza:
∫∫∫ ∇ • V dV = ∫∫ n • V dS
(A.125)
∫∫∫ ∇ • τ dV = ∫∫ n • τ dS
(A.126)
S = ∂V
V
S = ∂V
V
del rotore:
V
∫∫∫ ∇ ∧ V dV = ∫∫ n ∧ V dS
(A.127)
S = ∂V
V
n
Considerata la figura a lato vale il teorema di Stokes:
della circolazione:
∫∫ n • (∇ ∧ V ) dS = ∫ t • V dC = Γ
S = ∂V
C = ∂S
(A.128)
t
C
S
V
A.26
C.GOLIA – Fluidodinamica
A.11
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Cenni sui Sistemi di Coordinate Curvilinee non Ortogonali
Per poter presentare, nel modo più semplice che
possiamo immaginare, gli argomenti di algebra e di
calcolo
tensoriale
in
coordinate
curvilinee
[tradizionalmente ostici], adotteremo una presentazione
che farà riferimento sempre ad un sistema cartesiano, e
faremo ampiamente uso delle trasformazioni tra sistemi
di riferimento.
z
ξ3
z
ξ 2 =c 2
ξ1
Questo non è il percorso più breve, ma certamente il più
agevole per la comprensione.
ξ 1 =c 1
ξ2
ξ 3 =c 3
y
y
x
Consideriamo che ogni punto (x,y,z) del sistema
cartesiano Σ(x,y,z) può essere espresso come funzione di
altre variabili (ξ1,ξ2,ξ3):
x=x(ξ1,ξ2,ξ3)
x
y=y(ξ1,ξ2,ξ3)
z=z(ξ1,ξ2,ξ3)
(A.129)
Ovviamente il sistema di relazioni (A.129) dovrà essere invertibile (potrebbe non esserlo in certi punti
singolari, ma questo non è un vero problema in quanto escluderemo semplicemente l’uso di tali punti) e
capace di definire una corrispondenza univoca:
ξ1= ξ1 (x,y,z)
ξ2= ξ2 (x,y,z))
ξ3= ξ3 (x,y,z)
(A.130)
Le (A.129) e (A.130) definiscono un sistema di coordinate (in generale non necessariamente ortonormale)
curvilineo Σ(ξ1,ξ2,ξ3) e rappresentano anche la trasformazione tra il sistema cartesiano Σ(x,y,z) e quello
curvilineo Σ(ξ1,ξ2,ξ3) e viceversa.
Le superfici:
ξ1= ξ1 (x,y,z)=costante=c1,
ξ2= ξ2 (x,y,z)=costante=c2,
ξ3= ξ3 (x,y,z)=costante=c3,
(A.131)
sono le superfici coordinate del sistema Σ(ξ1,ξ2,ξ3) che passano per il punto (x,y,z) e le loro intersezioni
definiranno gli assi curvilinei che passano per il generico punto (x,y,z):
[ξ2 =c2 ] ∩ [ξ3 =c3 ]
[ξ3 =c3 ] ∩ [ξ1 =c1 ]
[ξ1 =c1 ]
∩ [ξ2 =c2 ]
→ asse curvilineo ξ1
→ asse curvilineo ξ2
(A.132)
→ asse curvilineo ξ3
Ci si pone il problema di trovare i versori coordinati del sistema Σ(ξ1,ξ2,ξ3) e le componenti di un generico
vettore a in questo sistema.
Per ragioni puramente didattici, assumeremo il vettore a(ax,ay,az) noto nel sistema Σ(x,y,z) e cercheremo di
esprimere le componenti di a nel sistema Σ(ξ1,ξ2,ξ3).
Ovviamente questo varrà anche per il vettore posizione: r(x,y,z) che nel sistema curvilineo avrà una
rappresentazione r(ξ1, ξ2, ξ3).
A.27
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
A scapito della generalità, ma a vantaggio della praticità, facciamo un esempio bidimensionale di un sistema
non ortogonale molto semplice (cui faremo riferimento per esempi pratici) rappresentato da due assi rettilinei
posti ad un generico angolo 0 < α < π.
In particolare nella figura è rappresentato un sistema non ortogonale
y
avente:
ξ2
• l’asse ξ1 parallelo all’asse x,
• l’asse ξ2 posto ad un angolo α rispetto all’asse x.
ξ(2)
Analizzando la figura notiamo, candidamente, che per il vettore
posizione r, si possono concepire due modalità di componenti rispetto
al sistema Σ(ξ1, ξ2):
y
ξ(2)
α
r
le intercette con le parallele all’altro asse [che abbiamo
ξ(1)
x,ξ(1)
indicato con indici:
ξ(1) ξ(2) ]
le intercette derivanti dalle proiezioni normali sull’asse [che abbiamo indicato con pedici:
ξ(2) ]
ξ1
x
ξ(1)
E’ ben ovvio che tale doppia modalità scompare (le due componenti coincideranno) se il sistema
Σ(ξ1, ξ2) fosse ortonormale (α=π/2).
Ed è altrettanto ovvio che i due tipi di componenti devono riferirsi a versori coordinati differenti.
Stiamo in pratica iniziando a scoprire i misteri delle componenti controvarianti e covarianti
Come in tutti i momenti di difficoltà osserviamo il consiglio del saggio: procedere con calma, metodo e
seguire i fondamentali.
•
•
•
•
Il vettore posizione r(x,y,z) ha, nel sistema curvilineo Σ(ξ1, ξ2, ξ3), una rappresentazione r(ξ1, ξ2, ξ3).
Il vettore tangente alla coordinata curvilinea ξ1 (per cui ξ2 e ξ3 devono essere costanti) nel punto
P(x,y,z) è dato per definizione da:
∂r
E (1) =
(A.133)
∂ξ1
Il versore tangente sarà:
E
E
e (1) = (1) = (1)
(A.134)
E (1) h (1)
Il fattore di scala relativo sarà:
h (1) ==
∂r
∂ξ1
(A.135)
Ovviamente lo stesso vale per le altre componenti tangenti (2) e (3).
Ma esiste un’altra possibilità: di considerare vettori normali alle direzioni coordinate.
• Queste sono definite dal gradiente della generica ascissa coordinata ξi.
• Ne discende quindi per il vettore normale alla ξ1:
(1)
= ∇ξ1
(1)
E
E
•
Il versore normale sarà:
e =
•
(1)
(A.136)
(1)
E
= (1)
(1)
h
E
(A.137)
Il fattore di scala relativo sarà:
A.28
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
h (1) = ∇ξ1
Ovviamente lo stesso vale per le altre componenti (2) e (3).
(A.138)
y
A questo punto dovrebbe essere chiaro che i versori e(i) sono
definiti paralleli agli assi coordinati mentre quelli e(i) sono
definiti normali agli assi coordinati ξi : cioè appaiono come
nella figura a lato (versione 2D).
ξ2
e (2 )
e (1 )
ξ1
e (2 )
e (1 )
Prima di procedere ulteriormente, conviene applicare quanto
ritrovato al semplice sistema di coordinate piane oblique e
verificare quanto intuito.
x
Nel dubbio che ci assale nell’esplicitare le relazioni delle coordinate del sistema obliquo rispetto a quello
cartesiano, ricordando i fondamentali, adottiamo la regola del parallelepipedo e quindi definiamo questo
sistema rispetto al cartesiano come:
x = ξ1 + ξ 2 cos α

 y = ξ 2 sinα
y

ξ1 = x − tan α

ξ = y
2
sinα

y
(A.139)
ξ2
(A.140)
α
x
ξ1
Nota: nella relazione inversa qualcosa sballa per α=0, ma non c’è problema: in questo caso i due assi ξ1=ξ2
coincidono e quindi il sistema di riferimento non è valido.
Dalle (A.139) si ricava per il vettore posizione r(ξ1,ξ2) nel riferimento cartesiano:
r = x i + y j = (ξ1 + ξ 2 cos α ) i + (ξ 2 sinα ) j
(A.141)
Ne discende per i vettori tangenti:
E (1) =
E ( 2) =
∂r
=i
∂ξ1
∂r
= cos α i + sin α j
∂ξ 2
h (1) = E (1) = 1
e (1) =
h (2 ) = E (2 ) = 1
e(2 ) =
E (1)
=i
h (1)
(A.142
E (2 )
= cos α i + sin α j (A.143)
h (2 )
e dalle (A.135) si ricava per l’altro set di vettori normali:
E
(1)
E
( 2)
1
j
= ∇ξ1 = i −
tan α
= ∇ξ 2 =
1
j
sin α
h
(1)
=E
(1)
2
1
 1 
= 1+ 
 =
sin α
 tan α 
1
(2 )
h (2 ) = E =
sin α
e
e
(1)
(2 )
= sin α i − cos α j (A.144)
=j
(A.145)
E’ interessante fare i diversi prodotti scalari tra i vari vettori tangenti e normali trovati:
A.29
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
1

(1)
E • E (1) =  i −
tan α


j  • (i ) = 1

(
(1)
E • E (1)
1
= (1)
(1)
h h (1)
h h (1)
)
e • e (1) = sin α i − cos α j • (i ) = sin α =
(1)
1

(1)
E • E (2 ) =  i −
tan α

(
(
(1)
)

j  • cos α i + sin α j = cos α − cos α = 0

)(
)
(1)
e • e (2 ) = sin α i − cos α j • cos α i + sin α j = sin α cos α − cos α sin α =
E • E (2 )
=0
h (1) h (2 )
 1 
• E1 = 
j • ( i ) = 0
 sin α 
(2 )
E •E
(2 )
e • e (1) = j • ( i ) = (2 ) (1) = 0
h h (1)
E
(2 )
()
E
e
(2 )
(2 )
 1
• E (2 ) = 
 sin α
() (
(
)

j  • cos α i + sin α j = 1

)
• e (2 ) = j • cos α i + sin α j = sin α =
E
(2 )
h
• E (2 )
(2 )
1
= (2 )
h (2 )
h h (2 )
Dalle formule ricavate notiamo che vale:
0 se i ≠ j
(i )
E • E ( j) = δ ij = 
1 se i = j
y
Questa rappresenta una relazione universale tra i vettori
tangenti e quelli normali.
j , e (2)
Nella figura a lato sono rappresentati questi versori nel
piano.
(A.146)
ξ2
α
e (2)
i , e (1)
ξ1
x
e (1)
A.11.1 Assi reciproci
Ma, ricordando i fondamentali, notiamo che la proprietà rappresentata dalla formula di cui sopra altro non è
che una relazione che lega una certa terna di assi:
E(1), E(2), E(3)
alla sua terna reciproca:
E(1), E(2), E(3)
Ma allora scopriamo che gli assi reciproci possono costruirsi, alternativamente, mediante i prodotti vettoriali
degli assi di partenza, ad esempio per i=1:
A.30
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
E
(1)
=
(2 )
E ( 2 ) ∧ E (3 )
E (1)
E (1) • (E (2 ) ∧ E (3 ) )
(3 )
E ∧E
= (1)
(2 )
(3 )
E • E ∧E
(
le altre relazioni si ottengono permutando gli indici [1-2-3] in senso positivo
)
(A.147)
.
Ma esiste, come sempre, una terza via, che preferiamo illustrare con un esempio di sistema curvilineo non
ortogonale leggermente più complicato.
Se consideriamo il sistema di coordinate curvilineo Σ(u1,u2) definito alle relazioni:
u1 = x y
;
u2=(x2+y2)/2
(A.148)
(rappresenta un sistema di iperboli-circonferenze)
x(u1,u2) e y(u1,u2).
avremo difficoltà nel ricavare esplicitamente le relazioni inverse:
Per cui, nel mentre sarebbe semplice costruirsi i vettori normali:
E
E
(1)
( 2)
= ∇u1 = =
= ∇u 2 =
∂u1
∂u
i+ 1 j
∂x
∂y
∂u 2
∂u
i+ 2 j
∂x
∂y
=
{
yi+x j
(A.149)
=
{
xi+y j
(A.150)
nella
fattispecie
nella
fattispecie
Avremmo difficoltà nel ricavare le espressioni dei vettori tangenti:
E (1) =
∂y
∂x
∂r
j
i+
=
∂u1
∂u1 ∂u1
E (2 ) =
∂j
∂x
∂r
j
i+
=
∂u 2
∂u 2 ∂u 2
(A.151
Con un poco di attenzione ai fondamentali, osserviamo che abbiamo a disposizione le derivare parziali delle
coordinate curvilinee rispetto a quelle cartesiane, cioè conosciamo lo jacobiano:
 ∂u1 ∂u 2 
∂ (u1 , u 2 )  ∂x
∂x 
(A.152)
=  ∂u
J=

∂ (x , y )  1 ∂u 2 
∂y 
 ∂y
e vogliamo calcolare le derivate parziali delle coordinate cartesiane rispetto a quelle curvilinee, cioè le
componenti della matrice che rappresenta l’inverso dello jacobiano di cui prima:
 ∂x
 ∂u
 1
 ∂x
 ∂u 2
∂y 
∂ (x , y )
∂u1 
=
= J −1
∂y  ∂ (u1 , u 2 )
∂u 2 
(A.153)
Per trovare queste componenti basta, quindi, invertire la matrice jacobiana. Questa inversa è pari alla matrice
aggiunta (composta dai complementi algebrici di ogni componente) divisa per il determinante.
Nel caso semplice considerato (2D) abbiamo una matrice 2x2, per cui:
A.31
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
 ∂x
 ∂u
 1
 ∂x
 ∂u 2
∂y 
 ∂u 2
1  ∂y
∂u1 
=
∂y  det(J )  ∂u 2
−
 ∂x
∂u 2 
 ∂x
 ∂u
 1
 ∂x
 ∂u 2
∂y 
 y − x
1
∂u1 
=
∂y  y 2 − x 2 − x y 
∂u 2 
∂u1 
∂y 

∂u1 
∂x 
−
(A.154)
Nel caso specifico si ricava quindi :
(
)
(A.155)
da cui
∂r
y
x
i− 2
j
= 2
2
∂u1 y − x
y − x2
x
y
∂r
E (2 ) =
i+ 2
j
=− 2
2
∂u 2
y −x
y − x2
E (1) =
(A.156
(A.157
Ovviamente anche in questo caso si ritrova (prova del nove) la relazione:
0 se i ≠ j
(i )
E • E ( j) = δ ij = 
1 se i = j
(A.158)
Queste relazioni sono molto utili perché consentono, ricordando il significato del doppio prodotto misto tra
vettori e l’espressione per lo jacobiano, di calcolare i volumi infinitesimi nelle due rappresentazioni di
coordinate:
(1)
(
(2 )
(3 )
)
dV (.) = d E • d E ∧ d E = h1h 2 h 3dξ1dξ 2 dξ 3
dV (.) = d E (1) • (d E (2 ) ∧ d E (3 ) ) = h1h 2 h 3dξ1dξ 2 dξ 3
controvariante
covariante
da cui discende la relazione:
(A.159)
(A.160)
dV (.)dV (.) = 1
(A.161)
A11.2 Componenti controvarianti e covarianti
A questo punto abbiamo tutti gli ingredienti per ricavare le definizioni delle componenti di un vettore a .
Possiamo definirle
rispetto ai vettori coordinati (E) (di lunghezza non necessariamente unitaria)
ovvero
rispetto ai versori coordinati (e) (di lunghezza certamente unitaria).
Ne derivano:
Componenti controvarianti: a(i):
A.32
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
3
(i )
a = A (1) E (1) + A ( 2 ) E (2 ) + A ( 3) E (3 ) = ∑ A ( i ) E (i ) ≡
{ A E (i )
i =1
dove:
A (i ) = a • E
(A.162)
notazione
indiciale
(i )
(A.163)
ovvero
3
(i )
a = a (1) e (1) + a ( 2) e (2 ) + a (3) e (3 ) = ∑ a ( i ) e (i ) ≡
{ a e (i )
i =1
dove:
a (i ) = a • e
(A.164)
notazione
indiciale
(i )
(A.165)
Componenti covarianti: a(i):
(1)
a = A (1) E + A (2 ) E
(2 )
+ A (3 ) E
(3 )
3
= ∑ A (i ) E
(i )
i =1
≡
{ A (i ) E
(i )
(A.166)
notazione
indiciale
dove:
A (i ) = a • E (i )
(A.167)
ovvero:
(1)
a = a (1) e + a (2 ) e
(2 )
+ a (3 ) e
(3 )
3
= ∑ a (i ) e
i =1
(i )
≡
{ a (i ) e
(i )
(A.168)
notazione
indiciale
dove:
a ( i ) = a • e (i )
(A.169)
Andiamo quindi a verificare, con ordine, le componenti controvarianti e covarianti di un generico vettore
a, per il nostro esempio di sistema di riferimento obliquo.
Dalle definizioni e da quanto ritrovato discende molto semplicemente:
Componenti (fisiche) controvarianti:
A (i ) = a • E
(i )
(A.170)
ay
1


j = a x −
A (1) = a x i + a y j •  i −
tan α 
tan α

ay
 1 
j =
A ( 2) = a x i + a y j • 
 sin α  sin α
Componenti controvarianti:
(
)
(A.171)
(
)
(A.172)
(i )
a (i ) = a • e
a (1) = (a x i + a y j) • (sin α i − cos α j) = a x sin α − a y cos α
(A.173)
a ( 2) = a x i + a y j • j = a y
(A.175)
(
Componenti (fisiche) covarianti:
) ()
A (i ) = a • E (i )
(
A ( ) = (a
)
j) • ( cos α i + sin α j) = a
(A.176)
A (1) = a x i + a y j • ( i ) = a x
2
x
i + ay
(A.174)
(A.177)
x
cos α + a y sin α
(A.178)
A.33
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Componenti covarianti:
a ( i ) = a • e (i )
(A.179)
(
)
a (2 ) = (a x i + a y j)• ( cos α i + sinα j) = a x cos α + a y sinα
a (1) = a x i + a y j • ( i ) = a x
(A.180)
(A.181)
y
Queste componenti sono riportate nella figura a lato.
ξ2
a (2)
a (2)
ay
a
α
x
a
(1)
a x,a (1)
ξ1
A.11.3 Variazione delle componenti di un vettore in sistemi curvilinei ruotati.
Dalle definizioni delle componenti controvarianti (A.170-172) e covarianti (A.176-178) discende che se
consideriamo due sistemi Σ e Σ’, ruotati l’uno rispetto all’altro, e indichiamo con qi’k il coseno dell’angolo
formato dall’asse i’ e l’asse k ovvero:
q ik' = E ( k ) • E
(i ')
q ik ' = E (i ) • E
'( k )
(A.182)
risulta:
•
•
per le componenti controvarianti:
A (i ' ) = q ik' A (k )
(A.183)
A (i ' ) = q ik' A (k )
(A.184)
per le componenti covarianti:
Il tipo di rappresentazione di un vettore rispetto ad un generico sistema curvilineo viene definito dal
soddisfacimento della regola di variazione delle sue componenti:
•
controvariante se si verifica l’osservanza delle (A.183),
ovvero
•
covariante
se si verifica l’osservanza delle (A.184).
Bada: ad essere pignoli, nell’esempio del sistema obliquo, le coordinate degli assi coordinati si dovrebbero
scrivere come ξ1 ed ξ2 in quanto il vettore posizione r ha una naturale rappresentazione
controvariante come:
r = ξ (1) E (1) + ξ ( 2 ) E (2 )
(A.185)
A.34
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
A.11.4 Il tensore metrico
Consideriamo le rappresentazioni controvariante e covariante, e definiamo le quantità:
(i )
g ik = E • E
g ik = E (i ) • E (k )
(k )
(A.186)
Ricordando le definizioni (A.173-175) e (A.179-181) e considerando i prodotti scalari:
a • e (i ) = a (k )
[e( ) • e( ) ]
k
(i )
a • e = a (k )
i
[e( ) • e( ) ]
k
i
(A.187)
risulterà che le componenti controvarianti di un vettore a potranno essere espresse in termini delle
componenti covarianti come:
a (i ) = g ik a (k )
(A.188)
ed analogamente le componenti covarianti di un vettore a potranno essere espresse in termini delle
componenti controvarianti come:
a (i ) = g ik a (k )
(A.189)
Le nove (in uno spazio 3D) componenti gik (ovvero gik) formano un tensore detto tensore metrico G che,
considerando i coefficienti metrici (o fattori di scala) hi si può esprimere come:
 g11 g12
G = g 21 g 22
g 31 g 32
g13   h1h1
g 23  = h 2 h1
g 33   h 3 h1
h 1h 2
h 2h 2
h 3h 2
h 1h 3 
h 2 h 3 
h 3 h 3 
(A.190)
ovviamente se il sistema curvilineo è ortogonale il tensore metrico sarà diagonale:
per sistemi ortogonali:
g11
G =  0
 0
NOTA:
0
g 22
0
2
0  (h1 )

0  =  0
g 33   0

Verificare che
gik=0 per i≠k
di un sistema di riferimento curvilineo.
0
(h 2 )
2
0
0 

0 
(h 3 )2 
(A.191)
è un buon metodo per testare l’ortonormalità
Il tensore metrico (talora chiamato tensore fondamentale perché definisce la forma bilineare fondamentale
o forma quadratica fondamentale della geometria algebrica) fornisce tutte le informazioni per
“l’algebrizzazione “ del sistema.
Una volta nota la base: E(1), E(2), E(3), l’elemento di arco tra due punti contigui sarà dato, per definizione, in
base alle (A.133) , da:
(ds )2 = d r 2 = d r • d r = g ik dξ (i )dξ (k )
(A.192)
e l’elemento differenziale di volume dV sarà:
A.35
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
dV = det (G )
NOTA:
dξ (1)dξ (2 )dξ (3 )
(A.193)
talora il determinante del tensore metrico G è denotato con G e la (A.159) si scrive:
dV = G dξ (1)dξ (2 )dξ (3 )
(A.194)
Nel caso di un sistema ortogonale, i coefficienti metrici, necessari per la definizione degli operatori, saranno:
h1 = g11
; h 2 = g 22
, h 3 = g 33
(A.195)
Come esempi: per il sistema di assi obliqui (2D) posti ad un angolo α si ritrova:
g12  (h1 )2
g
G =  11
=
g 21 g 22   h1h 2
cos α 
h 1h 2   1
=
2
(h 2 )  cos α 1 
(A.196)
G = 1 − (cos α ) = sin α
2
(A.197)
(ds )2 = (dξ1 )2 + (dξ 2 )2 + 2 cos α dξ1dξ 2
dA = sinα dξ1dξ 2 (elemento differenziale di area)
(A.198)
(A.199)
Mentre nel caso dell’esempio considerato per il sistema (2D) iperboli/circonferenze si ritrova:
 x 2 + y2

2
h1h 2   y 2 − x 2
=

(h 2 )2  − 2xy
2
2 2
 y − x
(
g12  (h1 )
g
G =  11
=
g 21 g 22   h1h 2
2
G=
(ds )2 =
)
(
(x
2
)
2
)
(y
2
−x
−x
dA =
)
2 2
)
2 2
y − x2
−x
x 2 + y2
2
)
2 2
− x2
)
2






1
2
2
(y
(A.200)
(A.201)
y − x2
2
1
2xy
2
2
[(dξ ) + (dξ ) ]−
1
2
=
(y
(y
2
+ y 2 − 4x 2 y 2
x 2 + y2
(y
−
4x y
2
− x2
)
2
dξ1dξ 2
dξ1dξ 2 (elemento differenziale di area)
(A.202)
(A.203)
Ovviamente verificandosi, in entrambi i casi, che i coefficienti del tensore metrico fuori diagonale sono non
nulli, ne deriva (come atteso) che i due sistemi saranno non ortogonali.
Esercizio A.1
Analizzare il sistema di riferimento polare-ellittico di cui alla (A.23)
Esercizio A.2
A.36
C.GOLIA – Fluidodinamica
Appendice A - Richiami di Calcolo vettoriale e tensoriale
Analizzare il sistema di riferimento curvilineo (3D)
x=u12+2,
y=u1+u2,
z=u32-1
Esercizio A.3
Esprimi il prodotto scalare tra due vettori a e b in termini delle loro componenti controvarianti e covarianti.
Trovarne l’espressione nel riferimento obliquo.
Esercizio A.4
Esprimi il prodotto vettoriale tra due vettori a e b in termini delle loro componenti controvarianti e
covarianti. Trovarne l’espressione nel riferimento obliquo.
Esercizio A.5
Date le basi: e1 = - 4 i +2 j
e2= 3 i +3 j
e3=2 k
Trova le componenti controvarianti e covarianti del vettore che va dall’origine al punto (1,1,1).
A.37