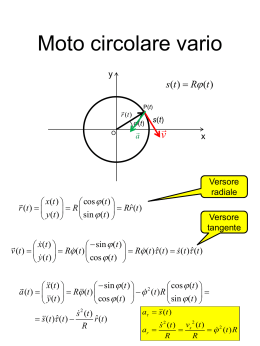
Velocità lungo la traiettoria
Vettori spostamento
successivi da P(t1)
P(t2)
P(t1)
P(t3)



r (t1 )

r (t2 )
r (t3 )
r (t4 )
Vettori posizione
O
P(t4)
r
vm 
t
Il vettore velocità media è parallelo al vettore
spostamento
Velocità lungo la traiettoria
Velocità
istantanea a t1
La velocità istantanea è
tangente alla traiettoria
Ascissa curvilinea
di P(t1)

P(t1)
P(t2)


s(t1)
P(t3)
P(t4)

r (t1 )
r (t2 )
r (t3 )
rDerivata
(t4 ) ascissa
curvilinea
Ω
v  vsˆ  sˆ
Velocità scalare
O
Versore
tangente
Modulo della velocità
| r |
corda
| v | lim
 lim
t 0 t
t 0
t
arco
| s | ds
lim
 lim

| s |
t 0 t
t 0 t
dt
Derivata di un vettore rispetto al
tempo
Differenza di due
vettori
Solo in componenti
cartesiane
 ax 
 
da
a (t  t )  a (t )
  ay 
 lim
dt t 0
t
a 
Vettore
Scalare  z 
• La derivata rispetto al tempo di un vettore è
un vettore
• Nella derivata variano sia il modulo che la
direzione del vettore primitivo
• Se cambia solo il modulo e non la direzione,
si dice che il vettore si allunga (si accorcia)
• Se cambia solo la direzione e non il modulo,
si dice che il vettore ruota
Moto del grave
• Il moto del grave è contenuto nel piano
verticale che contiene la velocità di esso
• Se la velocità è inizialmente lungo la
direzione verticale (o è nulla), il moto del
grave degenera in un moto rettilineo
 x(0)  vx (0)t

1 2  x(t )  

r (t )  r (0)  v (0)t  gt  
1 2

2
 z (t )   z (0)  vz (0)t  gt 

2


 x(t )   vx (0)
v (t )  v (0)  gt  


 
z
(
t
)
v
(0)

gt

  z

 x(t )   0 
a (t )  g  
     (cost.)
 z (t )    g 
g = 9,8 m/s2
L’asse x è orizzontale e l’asse z è verticale diretto verso
l’alto!
Il moto del grave è uniformemente accelerato
Traiettoria del grave
• La traiettoria si ottiene eliminando il
tempo dalle equazioni orarie del moto
 x  x(0)  vx (0)t


1 2
z

z
(0)

v
(0)
t

gt
z

2
Parabola con asse
verticale che passa
in P0=(x(0), y(0))
 x  x(0)
t  v (0)
x


2




 z  z (0)  v (0) x  x(0)  1 g x  x(0)




z

v
(0)
2
v
(0)
 x

 x


z  z (0)  b( x  x(0))  c( x  x(0))2
vz (0)

b

 tan 

v
(0)

x

g
c  g 

2vx 2 (0) 2v0 2 cos 2 
Modulo della
velocità iniziale
b, c costanti
vx (0)  v0 cos 

vz (0)  v0 sin 
Inclinazione sul
piano orizzontale
(angolo di alzo)
Moto circolare uniforme
• Moto lungo una circonferenza di raggio R
• velocità di modulo costante
y
P(t)
r (t )
•
 cos  (t ) 
rˆ(t )  

sin

(
t
)


φ(t)
O
x
Versore
radiale
Coordinate polari
Coordinate cartesiane
r (t )  R  cost.
 cos(t  0 ) 
 x(t ) 
r (t )  

R

  Rrˆ(t )

 y(t ) 
 sin(t  0 ) 
 (t )  t  0
  cost.
Moto circolare uniforme
Accelerazione
centripeta
s(t )  R (t )  R(0  t )
y
v
P(t)
r (t )
O
a
•
φ(t)
s(t)
 cos(t  0 ) 
 x(t ) 
r (t )  
  Rrˆ(t )
  R
 y(t ) 
 sin(t  0 ) 
x
Ascissa
curvilinea
Versore
radiale
Versore
tangente
  sin(t  0 ) 
 x(t ) 
v (t )  


R

   Rˆ(t )

 y(t ) 
 cos(t  0 ) 
cos(t  0 ) 
 x(t ) 
2 
2
a (t )  
   Rrˆ(t )
   R 
 y(t ) 
 sin(t  0 ) 
| r (t ) | R; | v (t ) ||  | R; | a (t ) |  2 R
Vettore
opposto al
versore
radiale