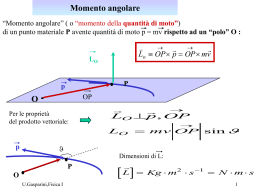
Moto dei pianeti
Il moto dei pianeti è descritto dalle tre leggi di Keplero, basate sulle osservazioni
dell’astronomo danese Tycho Brahe (1546-1601) ed assumendo
il punto di vista eliocentrico di Nicolo’ Copernico (1473-1543).
moto apparente di Marte
Marte
orizzonte delle
“stelle fisse”
Sole
Terra
Il moto apparente dei pianeti osservato da un sistema geocentrico (tolemaico)
è complicato: il modello cinematico che lo descrive è artificioso...
U.Gasparini, Fisica I
( “epicicli”, “deferenti”….)
1
Le tre leggi di Keplero:
1) I pianeti si muovono su orbite piane descrivendo
ellissi aventi il Sole in uno dei fuochi.
2.3 108 Km (  13 min-luce)
4.5 109 Km (  4 h 15 min -luce)
U.Gasparini, Fisica I
2
2a legge di Keplero
2) Il moto avviene con “velocità areale” costante
dA( t )
 costante
dt
( per un’orbita circolare :  v = cost. )
dA(t ) 

r (t )
1
r (t )ds(t ) sin 
2
t+d t

t+d t
t
v(t)
t
v(t)
Cio’ è conseguenza della conservazione del momento angolare :

LO = OP  mv
vr
v(t)
P
v
U.Gasparini, Fisica I
r(t)
ds
Lo  OP mv sin   mr
sin 
dt
dA
 m2
dt
Lo
dA
O ( Sole )
dt

2m
3
3a legge di Keplero
3) Il quadrato del periodo di rivoluzione è proporzionale al cubo
del semiasse maggiore dell’orbita:
3
T 2  kRmax
costante di Keplero
(caratteristica del sistema solare)
k  2.99  1019 s2 / m3
Esempio:
R Marte  228  106 Km
RTerra  149  106 Km

Il Sole visto da “Pathfinder”
TMarte  TTerra
 R Marte 


 RTerra 
3
 365
 228 


 149 
3
 691
giorni
“anno” marziano
U.Gasparini, Fisica I
4
Equazione di una traiettoria ellittica
In coordinate
polari:
semiasse maggiore
r ( ) 
 
a (1  e )
1  e cos
 0
rmin  a (1  e)

“eccentricità”

rmax  rmin
rmax  rmin
rsin
F2
F1 P  F2 P  2a
r

e 
P
2ae
F1



0 e 1
rmax  a (1  e)
r ( )
“Ellisse”:
circonferenza
2
F1 F2  rmax  rmin  2ae
a
r 2 sin 2   (2ae  r cos ) 2  2a
r 2 sin 2   ( 2ae  r cos  ) 2  ( 2a  r ) 2
r 2  4a 2 e 2  4aer cos  4a 2  4ar  r 2
ae 2  er cos  a  r
r (1  e cos  )  a (1  e 2 )
L’ipotesi newtoniana
Consideriamo un pianeta in orbita circolare intorno al Sole:
v
mP
FP =ma =mv2 /R
FS
M
Forza esercitata
dal Sole sul pianeta :
FP  mP a  mP
v2
4 2 R
4 2
 mP
 mP
2
R
T
kR 2
v 
Forza esecitata dal pianeta sul Sole :
FS  M

4
2
kpR
2
 FP
4 2
4 2

Mk
mP k P
U.Gasparini, Fisica I
2R
T

3a legge di Newton

costante universale

T 2  kR 3
4 2 m
4 2 M

k
kP
FP  
mP M
R2
6
Gravitazione universale
Newton verifico’ la sua ipotesi confrontando
l’attrazione gravitazionale esercitata dalla Terra sulla Luna
con quella esercitata sugli oggetti sulla superficie terrestre :
F  
MT
F
r2
r
ML
Stessa costante
universale
F 
U.Gasparini, Fisica I
M L MT
mM T
2
RT
 mg
Forza peso
sulla superficie della Terra
7
Per il moto di rivoluzione della Luna
intorno alla Terra:
F 
M L MT
 M La L
r2
2
 M L L
r

2 3
M T   L
r

g 
M T
2
RT

2
L
r3
2
RT
aL
r
RT
r  384000Km
RT  6400Km
L 
2
2
rad / giorno 
rad / s
27.5
27.5  86400

g  9,92m / s 2
U.Gasparini, Fisica I
, da confrontare col valore sperimentale
(al Polo):
g exp  9,83m /8 s 2
“Massa ridotta”
del sistema Terra-Luna :
accelerazioni assolute ( in un sistema inerziale)
Terra
MT 

aL  
aT
mL
Luna
a
L
a
Centro di massa CM
del sistema
d 
Terra-Luna
m
T
mL r
r

 RT

M
100
L
T
Accelerazione della Luna relativa alla Terra:
 M T  mL  
mL 






a ' L  a L  atr  a L  a T  a L 
aL  
 aL
MT
M


T



 
MT

aL  
aL '
 M T  mL 


 
MT

F  mL a L  mL 
aL ' 
 M T  mL 
U.Gasparini, Fisica I
“massa ridotta”:

mL M T
M T  mL

a L '
9
Considerando la massa ridotta del sistema Terra-Luna:
2
a L '   L
r  F 
mL M T
r2
accelerazione osservata dalla Terra



2 3
L
r   (mL  MT )
2 3
MT   L
r  mL
g 
M T
2
RT

2 3
L
r
2
RT
mL 

MT
80
m L
2
RT
 9 ,92  0.1  9 ,82 m / s 2
in accordo col valore sperimentale.
U.Gasparini, Fisica I
10