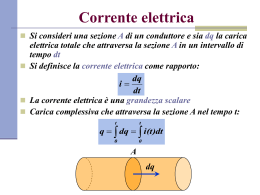
Fisica 2
Corrente continua
8a lezione
Programma della lezione
•
•
•
•
•
•
•
Corrente elettrica
Densità di corrente
Legge di Ohm, resistenza
Resistività, conduttività
Energia nei circuiti elettrici
Mobilità dei portatori
Composizione di resistenze
Corrente elettrica
• Per definizione è il rapporto tra la carica passata
attraverso una superficie e il tempo impiegato
Q
I
t
dq
• Corrente media e corrente istantanea I 
dt
• Esempi:
– corrente in un filo conduttore
– Corrente di un fascio di particelle
– Corrente ionica in un liquido
Corrente elettrica
• Alla corrente possono contribuire sia
cariche positive che negative
• I contributi si sommano se le velocità sono
opposte
• Il verso convenzionale della corrente è
quello della velocità delle cariche positive
Dimensioni fisiche. Unità di misura
• Le dimensioni della
corrente sono carica
diviso tempo
• L’unità di misura è
l’ampere (A) definito
come coulomb diviso
secondo
• Nel SI puro è il
coulomb ad essere
definito in termini di
ampere
I   QT
C
A
s
1
Corrente nei metalli
• In un oggetto metallico, alcuni degli elettroni più
esterni degli atomi costituenti vengono condivisi
da tutto l’oggetto
• Sono quindi liberi di muoversi entro l’oggetto,
ma vincolati a non lasciarlo da forze alla
superficie
• Posseggono un moto di agitazione termica che
è del tutto casuale → la velocità per diversi
elettroni o in diversi istanti assume le diverse
orientazioni possibili in modo casuale
• La velocità termica ha, in modulo, un valore
molto elevato
Corrente nei metalli
• L’applicazione di un campo E produce una
forza su tutti gli elettroni liberi, che di
conseguenza si muovono con una velocità
di deriva
• La velocità di deriva di tutti gli elettroni ha
la medesima direzione (opposta a E)
• La velocità di deriva ha valore piuttosto
piccolo
Corrente e densità dei portatori
• Consideriamo un filo metallico sede di corrente
stazionaria, di sezione (retta) costante A,
• sia n la densità di portatori
• e vd la velocità di deriva
vd t
vd t
• Il numero di portatori N che passa attraverso A nel
tempo t è pari al numero di portatori presenti nel
volume del cilindro di base A e altezza vd t
• La corrente è dunque
qN qnV
I

 nqvd A
t
t
A
Corrente e densità dei portatori
• Se la sezione non è retta, il volume è
V  vd tA cos a
• Dove a è l’angolo formato dai
 area A e velocità vd
 vettori
cioè:
V  vd  At
• La corrente si può allora scrivere:
   
qN qnV
I

 nqvd  A  J  A
t
t
• Ove è stato introdotto
 il vettore densità di corrente


J  nqvd  vd
• La corrente si può interpretare come il flusso del vettore
densità di corrente attraverso la sezione A
Densità di corrente
• Se il flusso di carica non è uniforme sulla sezione del
conduttore, possiamo generalizzare la definizione di
corrente come integrale del flusso della densità di corrente
sull’elemento di area della sezione
 
I   J  da
S
• Generalizzazione a più specie di portatori
 N

J   nk qk vk
k 1
Corrente attraverso superfici chiuse
• Relazione tra densità di carica e di corrente
dq
0
dt
i 0
• Conservazione della carica
 
d
dV
S J  da   dt 
(S )
i0
dq
0
dt
dq
i
dt
• Applicando il teorema della divergenza al primo
membro
 

  JdV   
dV

t
( S )
( S )
Equazione di continuità
• Dall’uguaglianza degli integrali, segue
 

 J  
t
• Se non c’è dipendenza dal tempo, si ha uno stato
stazionario:
 

t
0
 J  0
Densità di corrente
• Per un filo di sezione uniforme, il modulo è il
rapporto tra intensità di corrente e sezione retta
del filo
I
J
• Dimensioni
• Unità di misura
A
 nqvd
I  Q
J      2
 A  TL
C
u J   2
sm
Confronto tra velocità termica e di
deriva
• Velocità termica a 300 K
1
3
2
mvth  kT
2
2
1
2
3kT  3 1.38 10  23  300 
5

vth 
 

1
.
2

10
m/s
31

m
9.11 10


• Velocità di deriva in un filo di Cu di sezione
A=1mm2 per una corrente di 1A
I  nqAvd
vd 
I
1
5


7
.
4

10
m/s
28
19
6
nqA 8.47 10 1.6 10 10
Metalli - Legge di Ohm
• Lega la differenza di potenziale con l’intensità di
corrente in un conduttore metallico
I  KV
V  RI
• Le due grandezze V e I risultano proporzionali
– R: resistenza
– K: conduttanza
V 
• Dimensioni fisiche della resistenza R    
I 
V
W
• Unità di misura è l’ohm (W)
A
Resistività
• La resistenza dipende dalle
dimensioni geometriche
– lunghezza l, sezione A
• e dalla natura del conduttore
– resistività 
• Resistività
– Dimensioni
– Unità di misura
   RL 
l
R
A
RA

l
Wm
1
• Conduttività: è l’inverso della


resistività
• La resistività dipende dalla
  20 1  a 20 t  20
temperatura    (T )
Metalli – campo E dentro il filo
• Campo E in un filo conduttore a sezione costante
V0-V(x)
x
x
V0  V ( x)  iR ( x)  i
A
• Cioè V è proporzionale alla lunghezza, ne segue
che il campo è uniforme
V i
E 
 J
x A


E  J
Legge di Ohm microscopica
Metalli – relazione tra vd e E
• Risolvendo per i
i
A

E
• e dall’espressione della corrente in
i  qnvd A
funzione della velocità di deriva dei
portatori
E
• Segue che tale velocità è
vd 
 mE
proporzionale al campo
qn
– Il moto non è uniformemente accelerato,
come accade per una carica libera in un
campo E
– m: mobilità
Mobilità dei portatori
• Dimensioni
 1 
L3
L2 I  L2 I  L2 I T 2 QT
m     




2
ML
M
 qn  QRL QV  U 
• Unità
Cs
u m  
kg
Energia nei circuiti elettrici
• Consideriamo due punti 1 e 2 su di un filo
conduttore a potenziale V1 e V2 risp.
• Una carica Q passa da 1 a 2, l’energia
potenziale varia di U  QV2  QV1  QV2  V1   0
• Siccome la velocità dei portatori non cambia,
c’è una perdita netta di energia dei portatori
• Questa energia è ceduta agli ioni del reticolo
del conduttore e si manifesta come energia
termica: effetto Joule
• Energia fornita dal generatore
Potenza dissipata
• La potenza Joule è uguale
all’energia dissipata diviso il
E QV1  V2 
tempo
P

 IV
t
t
• È fornita dal generatore
elettrico
Q E  E 
P  IV  

• Dimensioni fisiche
T Q
T
• Unità di misura
• Forme alternative
C J J
u P   AV 
 W
s C s
2
V
P  IV  I 2 R 
R
Composizione di resistenze
• Composizione in serie. 1 e 2 sono
entrambe percorse dalla stessa
corrente I, ai capi di 1 c’è una
caduta di potenziale V1 e ai capi di
2 una caduta V2
• Vogliamo trovare una resistenza
equivalente all’insieme delle due,
nel senso che quando è percorsa
dalla stessa corrente I, troviamo ai
suoi capi la caduta di potenziale
V1+V2
• Cioè la resistenza equivalente è la
somma delle resistenze
V  IR
V1  V2  IR1  IR2
R  R1  R2
Composizione di resistenze
• Composizione in parallelo. 1 e 2
hanno una ugual caduta di
potenziale V ai loro capi e sono
percorse dalle correnti I1 e I2 risp.
• Vogliamo trovare una resistenza
equivalente all’insieme delle due,
nel senso che quando ai suoi
capi c’è la stessa caduta di
potenziale V essa è percorsa
dalla corrente I1+I2
• Cioè l’inverso della resistenza
equivalente è la somma degli
inversi delle resistenze 1 e 2
V
I
R
I1  I 2 
V V

R1 R2
1 1
1
 
R R1 R2