Superfici e volumi
Obiettivi
l
calcolare misure di superfici di poliedri
l
calcolare misure di superfici di particolari solidi di rotazione
l
calcolare volumi di poliedri
l
calcolare volumi di particolari solidi di rotazione
MATEMATICA, REALTAÁ E STORIA
Calcolare misure di superfici e volumi eÁ una delle cose che, anche senza
rendersene conto, si fa piuÁ spesso.
Si calcola quanta lamiera si deve usare per costruire le lattine che devono
contenere 550g di passata di pomodoro o 33cl di bibita (calcolo di una superficie noto il volume), si calcola quanta acqua puoÁ contenere un serbatoio di forma e dimensioni note, si studia che forma dare a un recipiente
in modo che possa contenere una data quantitaÁ di liquido utilizzando la minor quantitaÁ possibile di materiale.
L'uomo calcola superfici e volumi nella costruzione di edifici anche per rispettare le leggi e per ottimizzare le prestazioni energetiche. I Comuni stabiliscono infatti un definendolo come il
rapporto tra il volume dell'edificio che si vuole realizzare e la superficie
della zona stessa; nelle costruzioni di nuovi edifici questo limite non si
puoÁ superare.
Le prestazioni energetiche di un edificio sono molto influenzate dal rapporto tra il volume e la superficie esposta: a paritaÁ di volume, minore eÁ la superficie esposta, maggiori sono le prestazioni energetiche. La forma ideale
da dare a un edificio sarebbe quindi quella sferica (vedi un esempio nella
figura a lato), ma eÁ evidente che cioÁ non eÁ possibile; una buona alternativa
eÁ quella di costruzioni a forma di parallelepipedo, anche se si puoÁ intervenire con materiali adatti per poter creare forme piuÁ accattivanti dal punto di
vista estetico.
Anche la natura calcola superfici e volumi. In una cellula i processi metabolici hanno luogo in tutto il suo volume, ma la cellula deve essere in grado
di effettuare scambi con l'esterno attraverso la sua membrana, acquisendo
nutrimento ed espellendo scorie. Quando una cellula aumenta di dimensioni, il suo volume aumenta molto piuÁ rapidamente della superficie (per
esempio, raddoppiando il raggio di una sfera, il volume aumenta di otto volQ ISTITUTO ITALIANO EDIZIONI ATLAS
Padiglione americano all'Expo '67
disegnato da Buckminster Fuller
SUPERFICI E VOLUMI
1
te, mentre la superficie aumenta di quattro volte), quindi insorgerebbero difficoltaÁ negli scambi attraverso la membrana che non garantirebbe piuÁ la
quantitaÁ di nutrimento necessaria alla nuova massa. Esiste un rapporto ottimale superficie/volume oltre il quale la cellula si divide.
I nostri polmoni devono essere contenuti nel volume abbastanza piccolo
della cassa toracica, ma devono avere una grande superficie per poter rendere ottimale lo scambio di ossigeno con anidride carbonica; cosõÁ come anche il nostro intestino occupa un volume piccolo ma eÁ molto lungo, quindi
ha una grande superficie, aumentata anche dai villi intestinali.
Nel dare una dimensione a tutti gli esseri viventi, la natura stabilisce proporzioni ben definite tra volume e superficie perche la struttura del corpo di un
animale deve essere tale da sopportare lo sforzo di vivere in un ambiente
soggetto alla forza di gravitaÁ. Se un uomo diventasse molto, troppo alto,
avrebbe seri problemi a camminare perche le sue ossa e i suoi muscoli, cresciuti molto di piuÁ in lunghezza che in larghezza, non riuscirebbero a reggere il peso e si spezzerebbero. Ne sa qualcosa l'uomo piuÁ alto del mondo,
l'ucraino Leonid Stadnik, che con i suoi 2,57 metri di altezza necessita di
apparecchiature speciali per camminare.
Animali molto grandi, come per esempio la balenottera azzurra, che misura
fino a 33 metri e ha un peso equivalente a quello di 20 elefanti, possono
vivere solo in acqua, dove il loro peso viene attenuato dalla spinta dell'acqua stessa; fuori dal loro ambiente essi verrebbero schiacciati dal loro peso.
Divisione cellulare
Il problema da risolvere
Nei giochi si usano spesso i dadi e la caratteristica indispensabile di questo
oggetto eÁ che ogni faccia deve avere la stessa probabilitaÁ di uscire di tutte le
altre.
Quello che tutti conosciamo eÁ il dado a 6 facce che ha la forma di un cubo,
ma si possono realizzare dadi con meno o piuÁ facce utilizzando i solidi platonici; il dado di questo tipo con il massimo possibile di facce eÁ quello a
forma di icosaedro che ne ha 20.
Esistono peroÁ dadi corretti che hanno 24, 30, 48, 60 e addirittura 120 facce.
Nei giochi di ruolo si usano dadi con 30 facce a forma di rombo (figura 1);
un solido di questo tipo si chiama .
Le sue facce sono rombi che hanno una particolare caratteristica: il rapporto
tra la diagonale maggiore e la diagonale minore eÁ uguale alla sezione aup
1‡ 5
rea, cioeÁ vale
; i diedri formati da due facce consecutive misurano
2
144 .
p
Dimostra che la sua superficie ha area uguale a 12 52 e che il suo volume
q
p
eÁ uguale a 4 5 ‡ 2 53 , dove con si eÁ indicata la misura del lato del
rombo.
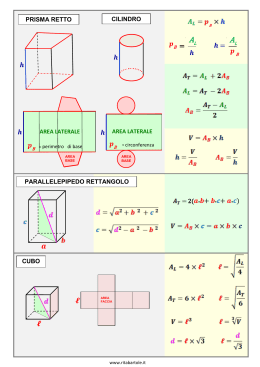
1. MISURE DI SUPERFICI
Figura 1
Gli esercizi di questo
paragrafo sono a pag. 20
1.1 Le superfici dei poliedri
Sappiamo che le facce dei poliedri sono poligoni; se immaginiamo di "aprire"
un poliedro e distendere le sue facce su un piano (osserva come esempio le
2
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
figure 2 e 3), possiamo calcolare l'area della sua superficie sommando le aree
di ciascun poligono.
Un discorso a parte deve essere fatto invece per i solidi di rotazione quali
cilindro, cono e sfera che non hanno delle facce poligonali da poter distendere su un piano. In questo caso dovremo enunciare assiomi appropriati
che, analogamente a quanto fatto nel piano per la determinazione della
lunghezza della circonferenza e dell'area del cerchio, ci porteranno alla
formulazione di regole. Nel seguito, indicheremo con ` l'area della superficie laterale, con quella di base, con quella della superficie totale di
un solido.
Il prisma
La superficie laterale di un prisma retto eÁ costituita da tanti rettangoli quanti sono i lati di base, aventi tutti la stessa altezza (figura 2a); la sua area si ottiene
quindi moltiplicando la misura del perimetro di base, che indicheremo con 2,
per quella dell'altezza ; la superficie totale si ottiene poi sommando a quella
laterale le aree delle due basi
` ˆ 2 ˆ ` ‡ 2
Nel caso particolare del parallelepipedo rettangolo, indicando con e le misure delle dimensioni del rettangolo di base e con quella dell'altezza, si ha
che (figura 2b)
` ˆ 2… ‡ † ˆ 2… ‡ † ‡ 2
Un'altra relazione importante da ricordare relativamente al parallelepipedo rettangolo eÁ quella che permette di calcolare la misura della sua diagonale.
Poiche i triangoli e sono rettangoli, applicando il teorema di Pitagora
si ha che (figura 2c):
q p
2
2
ˆ ‡ ˆ 2 ‡ 2
q p
2
2
e quindi ˆ ‡ ˆ 2 ‡ 2 ‡ 2
Figura 2
a.
b.
c.
La piramide
La superficie laterale di una piramide eÁ costituita da tanti triangoli quanti sono i
lati del poligono di base; se la piramide eÁ retta, sappiamo che le altezze di questi triangoli sono tutte congruenti e costituiscono l'apotema della piramide. In
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
3
questo caso, la superficie laterale si ottiene moltiplicando il semiperimetro del
poligono di base per l'apotema (figura 3); per avere la superficie totale basta
poi aggiungere l'area del poligono di base
` ˆ Figura 3
ˆ ` ‡ Se la piramide non eÁ retta, si dovraÁ calcolare l'area di ciascuna faccia e sommare poi i valori ottenuti.
Il tronco di piramide
Sezionando una piramide di vertice con un piano parallelo alla base otteniamo due solidi (figura 4):
l
l
una piramide piuÁ piccola 0 di vertice la cui base eÁ un poligono simile a
quello della piramide data (in colore rosa)
Figura 4
un secondo solido che chiamiamo tronco di piramide (in azzurro nella
stessa figura).
Le caratteristiche di questo solido sono le seguenti:
n eÁ delimitato da due basi che sono i due poligoni simili costituiti dalla base
della piramide data e dal poligono sezione;
n le sue facce laterali sono dei trapezi, in genere di basi e altezze diverse.
Se la piramide eÁ retta, sappiamo che le altezze delle facce laterali sono tutte
congruenti fra loro e costituiscono l'apotema; di conseguenza, anche le altezze
delle facce laterali del tronco di piramide sono tutte congruenti fra loro percheÂ
sono la differenza fra l'apotema della piramide data e l'apotema della piramide 0 . In questo caso, e a maggior ragione quando la piramide eÁ regolare,
l'area ` della superficie laterale del tronco di cono eÁ data dalla somma delle
aree dei trapezi che sono le facce laterali (figura 5):
` ˆ
ˆ
Figura 5
…1 ‡ 1 † …2 ‡ 2 †
… ‡ †
‡
‡ :::::::: ‡
ˆ
2
2
2
1 …1 ‡ 2 ‡ :::: ‡ † ‡ …1 ‡ 2 ‡ :::: ‡ †
2
dove i simboli indicano le misure delle basi minori di ciascun trapezio e i
simboli indicano le misure delle corrispondenti basi maggiori. In definitiva,
tenendo presente che la somma dei eÁ il perimetro 2 0 della base della piramide 0 e che la somma dei eÁ il perimetro 2 della base della piramide ,
l'area delle superficie laterale di un tronco di piramide retto eÁ uguale a
` ˆ
1
…2 0 ‡ 2 † ˆ … 0 ‡ †
2
dove evidentemente 0 e sono i semiperimetri dei due poligoni di base.
L'area della superficie totale eÁ poi la somma dell'area della superficie laterale con le aree e 0 dei due poligoni di base:
ˆ ` ‡ ‡ 0
I poliedri regolari
Abbiamo visto che tetraedro, ottaedro e icosaedro si ottengono dall'accosta-
4
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
mento di un certo numero di triangoli equilateri, il cubo dall'accostamento di
sei quadrati e il dodecaedro dall'accostamento di dodici pentagoni regolari (figura 6).
Figura 6
Sviluppo del tetraedro
Sviluppo dell'ottaedro
Sviluppo dell'icosaedro
Sviluppo del cubo
Sviluppo del dodecaedro
Per calcolare l'area delle superfici di questi solidi, indichiamo con lo spigolo
di ciascuno di essi e ricordiamo che:
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
5
p
3 2
l'area di un triangolo equilatero di lato eÁ
4
2
l'area del quadrato di lato eÁ l
l
1
l'area del pentagono regolare di lato eÁ uguale a 2
4
l
q
p
25 ‡ 10 5
Infatti congiungendo il centro del poligono con i vertici si ottengono triangoli
isosceli con l'angolo al vertice di 72 (figura 7); si ha cosõÁ che:
q
p
1
1
1
25 ‡ 10 5
ˆ ˆ cotan 36 ˆ
2
2
10
q
q
p 1
p
1
1
25 ‡ 10 5 ˆ 2 25 ‡ 10 5
area ˆ 5 2
10
4
Le superfici dei poliedri regolari sono quindi le seguenti (rivedi la figura 6):
p
3
`
hˆ
2
p
p
1
3
3 2
`ˆ
`
area ˆ ` 2
2
4
Figura 7
n area della superficie di un tetraedro (4 facce triangolari)
p
3 2 p 2
ˆ 3
ˆ4
4
n area della superficie di un ottaedro (8 facce triangolari)
p
p
3 2
ˆ 2 3 2
ˆ8
4
n area della superficie di un icosaedro (20 facce triangolari)
p
p
3 2
ˆ 5 3 2
ˆ 20 4
n area della superficie di un cubo (6 facce quadrate)
. ˆ 6 2
n area della superficie di un dodecaedro (12 facce pentagonali)
q
q
p
p
1 2
2
25 ‡ 10 5 ˆ 3 25 ‡ 10 5
ˆ 12 4
1.2 Le superfici dei solidi di rotazione
Il cilindro ed il cono
Per calcolare le superfici di questi solidi seguiremo un ragionamento analogo a
quello che eÁ stato fatto per arrivare alla determinazione della lunghezza della
circonferenza; in quel caso si era dimostrato che la classe dei poligoni inscritti
e quella dei poligoni circoscritti ad una circonferenza costituiscono una coppia
di classi contigue che ne definiscono la lunghezza. Cominciamo allora col dare alcune definizioni.
Un prisma retto si dice inscritto in un cilindro se le sue basi sono poligoni
inscritti nelle basi del cilindro; si dice circoscritto se le sue basi sono poligoni circoscritti alle basi del cilindro.
E' evidente che, avendo per basi dei poligoni regolari, un prisma regolare eÁ
sempre sia inscrittibile che circoscrittibile ad un cilindro; per questo motivo
considereremo nel seguito prismi regolari anche se cioÁ non eÁ indispensabile.
6
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Assumiamo come assioma la seguente proprietaÁ:
Assioma. La superficie laterale di un cilindro eÁ maggiore di quella di un
qualsiasi prisma inscritto e minore di quella di un qualsiasi prisma circoscritto.
Consideriamo allora l'insieme delle superfici laterali dei prismi regolari inscritti
e quello delle superfici laterali dei prismi regolari circoscritti ad un cilindro,
che indicheremo rispettivamente con e .
Questi insiemi sono:
n separati, percheÂ, essendo il perimetro di un poligono inscritto in una circonferenza minore del perimetro di un poligono ad essa circoscritto, anche la
superficie laterale di un prisma inscritto eÁ minore della superficie laterale
di un prisma circoscritto
n indefinitamente ravvicinati percheÂ, visto che eÁ sempre possibile trovare un
poligono inscritto ed un poligono circoscritto ad una circonferenza i cui perimetri hanno una differenza che puoÁ essere resa minore di un qualsiasi segmento piccolo prefissato, allora eÁ anche possibile trovare un prisma inscritto
ed un prisma circoscritto ad un cilindro tali che la differenza fra le loro superfici laterali possa essere resa piuÁ piccola di una qualsiasi altra superficie
piccola fissata.
Due insiemi A e B di grandezze omogenee sono:
l
l
separati se a < b
8a 2 A e 8b 2 B
indefinitivamente ravvicinati se:
8" > 0
9a 2 A ^ 9b 2 B:
b a<"
Se valgono queste proprietaÁ, la coppia …A, B† eÁ una
coppia di classi contigue.
Le classi e costituiscono quindi una coppia di classi contigue e ammettono percioÁ un unico elemento separatore. Tenendo conto dell'assioma enunciato, possiamo dire che
la superficie laterale di un cilindro eÁ l'elemento separatore della coppia di
classi contigue e .
La superficie laterale di un cilindro puoÁ quindi essere sviluppata in un rettangolo che ha per base la circonferenza rettificata della base e per altezza l'altezza del cilindro (figura 8); si giunge cosõÁ alle seguenti relazioni:
` ˆ 2
Figura 8
ˆ 2
‡ 2
2 ˆ 2
… ‡ †
Un analogo discorso vale per il cono. Diciamo che:
una piramide retta si dice inscritta o circoscritta ad un cono se il suo vertice
coincide con il vertice del cono e se la sua base eÁ rispettivamente inscritta o
circoscritta a quella del cono.
Analogamente a quanto detto per il prisma, una piramide regolare eÁ sempre sia
inscrittibile che circoscrittibile ad un cono; per questo, considereremo in seguito piramidi regolari.
Assumiamo come assioma la seguente proprietaÁ:
Assioma. La superficie laterale di un cono eÁ maggiore di quella di una qualsiasi piramide inscritta e minore di quella di una qualsiasi piramide circoscritta.
Allora, in modo del tutto analogo a quanto osservato per i prismi, possiamo dire
che
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
7
la classe delle superfici laterali delle piramidi regolari inscritte e quella delle
superfici laterali delle piramidi regolari circoscritte ad un cono costituiscono
una coppia di classi contigue che ammette come elemento separatore la superficie laterale di quel cono.
Figura 9
Questo significa che la superficie laterale di un cono eÁ equivalente ad un settore circolare che ha per base la circonferenza della base e per altezza l'apotema del cono (figura 9).
Valgono quindi le relazioni
ˆ ‡ 2 ˆ … ‡ †
` ˆ Figura 10
Il tronco di cono
In modo del tutto analogo a quanto fatto per il tronco di piramide, possiamo
definire un tronco di cono come quel solido che si ottiene togliendo da un cono il cono 0 che si ha sezionando con un piano parallelo alla base; i due
cerchi sono le basi, la differenza fra gli apotemi dei due coni rappresenta l'apotema del tronco (figura 10).
La superficie laterale di un tronco di cono si definisce in modo analogo a quella del cono, come elemento separatore della coppia di classi contigue costituite dai tronchi di piramide inscritti e circoscritti al tronco stesso.
Lo sviluppo della superficie laterale di questo solido eÁ quindi quella in figura
11 e si puoÁ calcolare togliendo dalla superficie laterale del cono completo la superficie laterale del cono 0 . Se indichiamo con e le misure dei raggi
delle due circonferenze di base, si dimostra che la misura ` della sua area eÁ
data dalla formula
` ˆ
1
…2
‡ 2† ˆ …
‡ †
2
Figura 11
L'area della superficie totale di conseguenza eÁ uguale a:
ˆ …
‡ † ‡ 2 ‡ 2
a.
La sfera
La superficie sferica, a differenza di quella del cilindro e di quella del cono,
non si puoÁ sviluppare su un piano; per questo, giungere alla determinazione
della sua area non eÁ cosõÁ immediato.
Sembra che giaÁ Archimede avesse scoperto che l'area di una superficie sferica
fosse quattro volte l'area del cerchio massimo e Galileo trovoÁ poi lo stesso risultato per via sperimentale. Egli costruõÁ una superficie sferica ed il relativo cerchio massimo con una lamiera omogenea, ovunque dello stesso spessore, e pesoÁ poi i due oggetti trovando che il peso della superficie sferica eÁ quattro volte
quello del cerchio massimo.
Noi cercheremo di giungere a questo risultato per via geometrica.
b.
Figura 12
Cominciamo con l'osservare che un arco di circonferenza che ruota di una rotazione completa attorno ad un diametro che non la interseca, come in figura
12, genera una zona sferica, oppure una calotta nel caso limite in cui un estremo dell'arco coincida con uno degli estremi del diametro.
8
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Consideriamo adesso una poligonale inscritta nell'arco considerato che abbia i
lati e gli angoli congruenti fra loro ed una analoga poligonale circoscritta all'arco (figura 13); tali poligonali si dicono regolari e la distanza dei lati della poligonale inscritta dal centro della circonferenza si chiama apotema della poligonale.
Sappiamo che la lunghezza della poligonale inscritta eÁ minore della lunghezza
dell'arco che, a sua volta, eÁ minore della lunghezza della poligonale circoscritta; siamo quindi portati ad accettare il seguente assioma:
Figura 13
Assioma. La superficie di una zona sferica generata dalla rotazione completa
di un arco di circonferenza attorno ad un diametro eÁ sempre minore della
superficie generata dalla rotazione di una poligonale regolare circoscritta all'arco ed eÁ sempre maggiore della superficie generata dalla rotazione di una
poligonale regolare inscritta nell'arco.
Se adesso consideriamo la classe delle superfici ottenute facendo ruotare le
poligonali regolari inscritte con un sempre maggiore numero di lati e la classe
delle superfici ottenute facendo ruotare le poligonali regolari circoscritte,
con ragionamenti simili a quelli fatti nel caso di cilindro e cono, possiamo dimostrare che e sono una coppia di classi contigue; allora possiamo definire la superficie di una zona sferica come l'elemento separatore di tale coppia
di classi.
Se riusciamo a trovare l'area delle superfici e , abbiamo trovato anche l'area di una zona sferica.
Si puoÁ dimostrare che valgono le seguenti proprietaÁ.
n Consideriamo, in uno stesso piano, un segmento ed una retta che non
intersechi se non in uno dei suoi estremi; ruotando intorno a , genera una superficie . Indichiamo con il punto medio del segmento
, con l'intersezione dell'asse di rotazione con la perpendicolare per
ad , e infine con 0 e 0 le proiezioni di e sull'asse di rotazione
(figura 14).
L'area di eÁ uguale al prodotto della misura della circonferenza che ha per
raggio per la misura del segmento 0 0 :
Figura 14
Area… † ˆ 2 0 0
Conseguenza immediata di cioÁ eÁ che:
n l'area della superficie generata da una poligonale regolare che ruota attorno ad un asse passante per il centro della circonferenza e che non la incontra eÁ uguale al prodotto della misura della circonferenza che ha per raggio
l'apotema della poligonale per la misura ` della proiezione della poligonale sull'asse di rotazione. Con riferimento alla figura 15
ˆ 2`
Figura 15
con ` ˆ 0 0
Infatti, per la precedente proprietaÁ, l'area della superficie generata dalla rotazione di eÁ 2 0 0 , l'area generata dalla rotazione di eÁ 2 0 0 e cosõÁ via. Sommando le varie parti e tenendo presente
che i segmenti , , ...., sono congruenti e rappresentano l'apotema
della poligonale, si ottiene l'area cercata:
ˆ 2 … 0 0 ‡ 0 0 ‡ 0 0 ‡ :::† ˆ 2`
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
9
Ragioniamo adesso in questo modo: se aumentiamo il numero dei lati della poligonale, l'apotema tende ad essere uguale al raggio della circonferenza,
quindi l'area della superficie generata dalla poligonale diventa 2
`. Ma ` eÁ
l'altezza della zona, quindi possiamo concludere che
l'area di una zona o di una calotta sferica di una sfera di raggio eÁ uguale al
prodotto della misura della circonferenza massima per la misura della sua
altezza :
ˆ 2
A questo punto, visto che la sfera puoÁ essere considerata come una calotta di
altezza 2
, possiamo concludere che l'area di una superficie sferica eÁ data da
Figura 16
S ˆ 2
r 2r ˆ 4
r 2
cioeÁ l'area di una superficie sferica eÁ uguale a quattro volte l'area del cerchio
massimo.
Si puoÁ inoltre dimostrare che l'area di un fuso sferico di una sfera di raggio ,
delimitato da due piani che definiscono un diedro di ampiezza (figura 16), eÁ
dato dalla formula:
ˆ 2
2
2
ˆ
90
se eÁ espresso in radianti
se eÁ espresso in gradi
VERIFICA DI COMPRENSIONE
1. Scegli fra quelle indicate la formula corretta per calcolare:
a. la superficie laterale di un prisma retto:
¬ b. la superficie laterale di una piramide retta:
c. la superficie di un cubo di spigolo `:
d. la superficie di un tetraedro di spigolo `:
e. la superficie totale di un cilindro:
f. la superficie totale di un cono:
¬
¬
¬
¬
¬
4`2
p
4 3`2
…
‡ †
…
‡ †
­ 2
®
­
­
­
­
­
®
®
®
®
®
2. MISURE DI VOLUMI
Il concetto di area riferito a superfici piane come caratteristica che hanno in
comune tutte le superfici equivalenti, nello spazio si trasforma nel concetto
di volume, inteso come caratteristica che hanno in comune tutti i solidi che occupano la stessa parte di spazio.
In questo paragrafo vogliamo vedere come calcolare il volume dei solidi di cui
ci siamo occupati finora. Cominciamo col dire che, se nel piano abbiamo assunto come unitaÁ di misura delle superfici un quadrato di lato prefissato , nello spazio assumeremo come unitaÁ di misura un cubo di spigolo . Premettiamo
il seguente teorema.
2
`2
p 2
3`
2…
‡ †
… ‡ †
2
3
6`2
3`2
2
…
‡ †
2
…
‡ †
Gli esercizi di questo
paragrafo sono a pag. 25
Teorema. I volumi di parallelepipedi rettangoli aventi basi congruenti sono
proporzionali alle rispettive altezze.
10
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Dimostrazione.
Figura 17
Con riferimento alla figura 17, consideriamo i parallelepipedi 1 , 2 , 3 , .... che
hanno tutti la stessa base. Ricordiamo che il criterio generale di proporzionalitaÁ
afferma che due insiemi di grandezze sono direttamente proporzionali se e solo se si conserva la congruenza e la somma; nel nostro caso, se due parallelepipedi che hanno la stessa base hanno altezze congruenti, allora sono congruenti; inoltre se l'altezza di un parallelepipedo eÁ la somma delle altezze di
altri due, per esempio 3 ˆ 1 ‡ 2 , allora anche il parallelepipedo 3 eÁ la somma dei parallelepipedi 1 e 2 . I due insiemi di grandezze sono quindi proporzionali.
§
Possiamo adesso dimostrare che:
Teorema. Il volume di un parallelepipedo rettangolo eÁ dato dal prodotto delle misure delle sue dimensioni.
Dimostrazione.
Consideriamo il parallelepipedo rettangolo di dimensioni , , e indichiamo
con (, , ) il suo volume; sia poi (!, !, !) il volume del cubo di spigolo
!; consideriamo poi i parallelepipedi rettangoli di dimensioni , , ! il cui volume eÁ (, , !) e , !, ! il cui volume eÁ (, !, !) (figura 18).
Per il teorema precedente possiamo dire che
…, , †
ˆ
…, , !†
!
i due parallelepipedi hanno entrambi le basi di dimensioni e e le altezze sono e !
…, , !†
ˆ
…, !, !†
!
i due parallelepipedi hanno entrambi le basi di dimensioni e ! e le altezze sono e !
…, !, !†
ˆ
…!, !, !†
!
i due parallelepipedi hanno entrambi le basi quadrate
di dimensione ! e le altezze sono e !
Figura 18
Moltiplicando membro a membro queste tre relazioni segue che
…, , †
ˆ
…!, !, !†
! ! !
esprime la misura della dimensione rispetto all'unitaÁ ! ed ana!
logamente gli altri rapporti esprimono le misure delle dimensioni e rispetto
…, , †
alla stessa unitaÁ di misura; il rapporto
esprime la misura del volu …!, !, !†
me del parallelepipedo dato rispetto al cubo preso come unitaÁ di misura. Indicando con il volume del parallelepipedo e con , , le misure delle dimensioni del parallelepipedo, si ha allora che
Il rapporto
ˆ
§
Nel caso particolare in cui il parallelepipedo sia un cubo il cui spigolo misura
, si ha che ˆ 3 .
Abbiamo cosõÁ trovato una regola per calcolare il volume di un parallelepipedo
rettangolo e di un cubo. Vediamo ora come procedere per trovare analoghe
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
11
regole per gli altri solidi. Come nel piano, anche nello spazio diremo che
due figure sono equivalenti se hanno la stessa estensione.
Il confronto fra figure nello spazio per vedere se hanno la stessa estensione,
cioeÁ se sono equivalenti, si serve di un assioma che prende il nome di Principio
di Cavalieri e che si basa sulle seguenti considerazioni.
Consideriamo due solidi che abbiano la base sullo stesso piano e consideriamo tutti i possibili piani paralleli ad (in figura 19 ne abbiamo disegnato
uno); le sezioni dei due solidi con tali piani possono essere poligoni diversi fra
loro, ma se hanno la stessa area, cioeÁ se sono equivalenti a coppie, eÁ logico
pensare che la loro sovrapposizione generi due solidi che hanno la stessa
estensione. Enunciamo allora il seguente assioma.
Figura 19
Principio di Cavalieri. Se due solidi si possono disporre in modo che siano
equivalenti le sezioni con ogni piano parallelo ad un piano fissato, essi
sono equivalenti.
Il principio di Cavalieri ci permette di dimostrare alcuni teoremi di equivalenza
che ci consentiranno di giungere facilmente al calcolo delle misure dei volumi
dei principali solidi.
Due prismi che hanno basi equivalenti ed altezze congruenti sono equivalenti.
Dimostrazione.
Collochiamo i due prismi su uno stesso piano come in figura 20 e sezioniamo i due solidi con un piano parallelo ad . Le sezioni ottenute sono congruenti alle basi dei due solidi e, poiche le due basi sono equivalenti per ipotesi, anche le sezioni lo sono.
Allora, per il principio di Cavalieri i due prismi sono equivalenti.
§
Figura 20
Due piramidi che hanno basi equivalenti ed altezze congruenti sono equivalenti.
Dimostrazione.
Operiamo come nel caso precedente disponendo le due piramidi sullo stesso
piano come in figura 21 e sezioniamo poi i due solidi con un piano parallelo ad . Indichiamo con e le basi delle due piramidi e con 0 e 0 i rispettivi poligoni sezione ottenuti.
Tali poligoni sono simili alla base della propria piramide e, poiche si trovano
alla stessa distanza dal piano della base, il rapporto di similitudine eÁ lo stesso
nelle due piramidi; indichiamo con " tale rapporto.
Sappiamo che se due poligoni sono simili di rapporto ", le loro aree stanno nel
rapporto " 2 , quindi possiamo dire che
area… 0 †
ˆ "2
area…†
cioeÁ, confrontando i due rapporti
12
SUPERFICI E VOLUMI
e
Figura 21
area… 0 †
ˆ "2
area…†
area… 0 †
area… 0 †
ˆ
area…†
area… †
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Questo significa che, se e sono equivalenti, anche 0 e 0 lo sono.
Dunque, per il principio di Cavalieri, le due piramidi sono equivalenti.
§
Una piramide eÁ equivalente alla terza parte di un prisma che ha la base congruente a quella della piramide e la stessa altezza.
Dimostrazione.
Consideriamo dapprima una piramide a base triangolare e operiamo la
seguente costruzione (figura 22):
Figura 22
n tracciamo per il vertice il piano parallelo alla base della piramide
n tracciamo da e da le parallele allo spigolo che incontrano rispettivamente in # e in $ il piano n congiungiamo poi # ed $ con .
Considerando che, per la costruzione fatta, i triangoli e #$ sono congruenti, quello che abbiamo ottenuto eÁ un prisma che ha per base la base della
piramide e per altezza l'altezza della piramide.
Se ora tracciamo anche il piano $, il prisma rimane suddiviso nelle tre piramidi , $# e $.
Osserviamo che le prime due piramidi sono equivalenti perche hanno congruenti le basi e #$ e le rispettive altezze; le piramidi $# e $ sono anch'esse equivalenti perche hanno le basi #$ e $ congruenti e la stessa
altezza. In definitiva le tre piramidi considerate sono equivalenti fra loro.
Allora la piramide a base triangolare considerata eÁ la terza parte di un prisma
che ha la stessa base e la stessa altezza di quella della piramide.
Osserviamo ora che una piramide che ha per base un poligono qualsiasi puoÁ
sempre essere vista come la somma di piuÁ piramidi a base triangolare; basta
infatti tracciare le diagonali del poligono uscenti da un vertice e considerare
i tetraedri che hanno per base i triangoli ottenuti e per vertice il vertice della
piramide (figura 23). Ciascuno di questi tetraedri eÁ equivalente alla terza parte
di un prisma che ha per base quel triangolo e per altezza l'altezza della piramide. La somma dei tetraedri, cioeÁ la piramide, eÁ allora equivalente alla terza
parte della somma dei prismi, ma la somma dei prismi eÁ un prisma che ha per
base la base della piramide e per altezza la stessa altezza. Resta quindi dimostrato l'enunciato del teorema.
§
Figura 23
In modo del tutto analogo, sezionando con dei piani paralleli alla base e controllando l'equivalenza delle figure piane ottenute, si dimostra che valgono anche i seguenti teoremi.
Un cilindro ed un prisma sono equivalenti se hanno le basi equivalenti e la
stessa altezza.
Un cono ed una piramide sono equivalenti se hanno le basi equivalenti e la
stessa altezza.
Le formule per il calcolo dei volumi
I teoremi di equivalenza che abbiamo visto ci permettono di trovare delle formule per esprimere la misura del volume di uno dei solidi che abbiamo studiaQ ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
13
to. Possiamo infatti ricondurci in ogni caso al calcolo della misura del volume
di un parallelepipedo a noi giaÁ nota.
Indicando con la misura dell'area di base e con quella dell'altezza si ha che:
n poiche un prisma eÁ equivalente ad un parallelepipedo avente la base equivalente a quella del prisma e la stessa altezza, la misura del volume di un
prisma si calcola con la formula
prisma ˆ n poiche una piramide eÁ equivalente alla terza parte di un prisma avente la
stessa base e la stessa altezza, la misura del volume di una piramide si calcola con la formula
1
piramide ˆ 3
n poiche un cilindro eÁ equivalente ad un prisma avente la base equivalente a
quella del prisma e la stessa altezza, la misura del volume di un cilindro si
calcola con la formula
cilindro ˆ cioeÁ
cilindro ˆ 2 n poiche un cono eÁ equivalente ad una piramide avente la base equivalente a
quella del cono e la stessa altezza, la misura del volume di un cono si calcola con la formula
cono ˆ
1
3
cioeÁ
cono ˆ
1 2
3
n il volume di un tronco di piramide si puoÁ calcolare sottraendo dal volume
della piramide il volume della piramide 0 (rivedi la figura 4). Supponendo di conoscere le misure e delle aree delle due basi minore e maggiore
del tronco e quella della sua altezza si dimostra che tale volume eÁ uguale
a (vedi a questo proposito l'esercizio guida n. 1 nella parte riservata agli
esercizi sulle competenze)
tronco di piramide ˆ
p
1
‡ ‡ 3
n il volume di un tronco di cono si puoÁ calcolare sottraendo dal volume del
cono il volume del cono 0 (rivedi la figura 10). Supponendo di conoscere le misure e dei raggi dei cerchi che costituiscono le basi del tronco e
quella della sua altezza si dimostra che tale volume eÁ uguale a (vedi a
questo proposito l'esercizio guida n. 2 dello stesso gruppo)
tronco di cono ˆ
Figura 24
1
…
2 ‡ 2 ‡ †
3
Valutiamo adesso il volume della sfera. Consideriamo dunque una sfera di centro e raggio , il cilindro equilatero ad essa circoscritto e i due coni che hanno
per basi le basi del cilindro e per vertice il centro della sfera (figura 24). Il solido
che si ottiene togliendo dal cilindro i due coni prende il nome di anticlessidra.
Dimostriamo che vale il seguente teorema.
14
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Una sfera eÁ equivalente all'anticlessidra.
Dimostrazione.
Come nei casi precedenti, sezioniamo la figura costruita con un piano parallelo
alla base (figura 25). Se tale piano passa per il centro della sfera, allora la sezione della sfera eÁ il cerchio massimo, la sezione dell'anticlessidra eÁ ancora il
cerchio massimo e quindi le due sezioni sono equivalenti.
Se il piano non passa per il centro, la sezione che si ottiene dalla sfera eÁ un
cerchio di raggio , quella che si ottiene dall'anticlessidra eÁ la corona circolare delimitata dai cerchi di raggi e .
L'area del cerchio di raggio eÁ L'area della corona circolare eÁ Figura 25
2
2
2
Osserviamo adesso che eÁ proprio il raggio della sfera (pertanto
ˆ ˆ † e che, visto che il cono ha il raggio di base congruente all'altezza, anche  . Inoltre, se applichiamo il teorema di Pitagora al trian2
golo , si ha che ˆ 2
2
ˆ 2
2
2
. Da tutto cioÁ deriva che:
2
cioeÁ
2
2
ˆ 2
Allora il cerchio sezione del piano con la sfera eÁ equivalente alla corona circolare sezione del piano con l'anticlessidra; per il principio di Cavalieri la sfera e
l'anticlessidra sono quindi equivalenti.
§
Il teorema dimostrato ci indica il modo di calcolare la misura del volume di
una sfera:
sfera ˆ cilindro 2cono
cilindro ˆ 2 2
ˆ 2
3
ed essendo
si ha che
sfera ˆ 2
3
2
cono ˆ
1 2
1
ˆ 3
3
3
1 3 4 3
ˆ 3
3
Figura 26
I volumi delle parti della sfera
Abbiamo detto nel precedente capitolo che un settore sferico eÁ definito dalla
rotazione completa di un settore circolare attorno alla retta di un diametro
che non lo attraversa.
In figura 26a mostriamo il caso in cui il settore ruota attorno alla retta del diametro passante per , mentre in figura 26b eÁ il settore che ruota
attorno alla retta di un diametro qualsiasi (che non lo attraversa).
Si dimostra che il volume di un settore sferico eÁ dato dal prodotto di un terzo
del raggio della sfera per l'area della calotta oppure della zona sferica corrispondenti:
settore sferico ˆ
a.
1
(area della calotta o della zona sferica)
3
Poiche abbiamo visto che l'area della calotta o della zona eÁ uguale a 2
, il
volume si puoÁ esprimere sinteticamente con la formula
settore sferico ˆ
1
2
2
ˆ 2 3
3
Q ISTITUTO ITALIANO EDIZIONI ATLAS
b.
SUPERFICI E VOLUMI
15
Questa formula ci permette di calcolare facilmente il volume di un segmento
sferico.
n Il volume di un segmento sferico a una base si ottiene togliendo (o aggiungendo a seconda dei casi) dal volume del corrispondente settore sferico il
volume del cono che ha per base la base del segmento e vertice nel centro
della sfera (figura 27); sviluppando i calcoli (vedi a questo proposito l'esercizio guida n. 3 nella parte riservata agli esercizi sulle competenze) si giunge alla formula:
segmento sferico a una base ˆ
1 2
…3
3
†
n Il volume di un segmento sferico a due basi si ottiene come differenza di
due segmenti sferici a una base (figura 28); con metodi analoghi al precedente (vedi l'esercizio n. 4 nella parte riservata agli esercizi dello stesso
gruppo) si arriva alla formula:
segmento sferico a due basi ˆ
Figura 27
Figura 28
1
1
12 ‡ 22 ‡ 3
2
6
essendo l'altezza del segmento, 1 e 2 i raggi delle due basi.
Il volume di uno spicchio sferico di ampiezza (rivedi la figura 16) si calcola
con le formule:
2 3
3
ˆ 3
270
spicchio sferico ˆ
se eÁ espresso in radianti
spicchio sferico
se eÁ espresso in gradi
VERIFICA DI COMPRENSIONE
1. Completa:
a.
b.
c.
d.
16
due prismi sono equivalenti se .......................
una piramide e un prisma hanno basi equivalenti; i due solidi sono equivalenti se ....................
un cilindro e un cono hanno basi equivalenti; i due solidi sono equivalenti se ..........................
se da un cilindro equilatero si tolgono i due coni aventi ciascuno per base una base del cilindro e per
altezza un segmento congruente alla metaÁ dell'altezza del cilindro si ottiene .....................
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Per il calcolo della superficie basta calcolare l'area di un rombo; indicando con % la semidiagonale maggiore e con & la semidiagonale minore sappiamo che (figura 29):
p
8
%
1
‡
5
>
< ˆ
per le ipotesi fatte
&
2
>
: 2
% ‡ & 2 ˆ 2
applicando il teorema di Pitagora
s
s
p
p
5‡ 5
5
5
Risolvendo il sistema troviamo che: % ˆ
e &ˆ
.
10
10
L'area di una faccia eÁ:
La risposta al
quesito iniziale
Figura 29
s
p s
p
p
5‡ 5
5
5
2 5 2
2
ˆ
10
10
5
L'area della superficie del solido eÁ quindi:
p
p
2 5 2
ˆ 122 5.
30 5
Figura 30
Il calcolo del volume eÁ un po' piuÁ complesso. Possiamo immaginare che il
triacontaedro sia formato da 30 piramidi che hanno per base una faccia le
cui altezze convergono tutte in un punto che eÁ il centro del poliedro
(figura 30); il volume si puoÁ quindi calcolare sommando i volumi di tutte
queste piramidi.
Per il calcolo dell'altezza ragioniamo cosõÁ (figura 31):
dal centro del rombo di base tracciamo la perpendicolare al lato; la
misura di questo segmento eÁ data dall'espressione
r
p r
p
5‡ 5
5
5
p
5
10
10
ˆ
ˆ
5
, cioeÁ:
Figura 31
poiche due facce consecutive del solido formano un angolo di 144 , la
faccia laterale della piramide forma un angolo di 72 con il piano della
base; questa eÁ quindi l'ampiezza dell'angolo che l'apotema della
piramide forma con il segmento l'altezza della piramide si ottiene quindi applicando il secondo teorema sui triangoli rettangoli al triangolo :
p q
p
5
5‡2 5
ˆ tan 72 ˆ
5
Possiamo adesso calcolare il volume del solido:
p q
p
q
p
p 3
5
1 2 5 2
ˆ |‚‚‚‚30
{z‚‚‚‚} 3 5 5 5 ‡ 2 5 ˆ 4 5 ‡ 2 5
|‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚{z‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚‚}
numero piramidi
volume di una piramide
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
17
I concetti e le regole
Le superfici dei poliedri
Per calcolare la misura della superficie di un poliedro basta sviluppare tale superficie in un piano e calcolare le aree
dei poligoni cosõÁ ottenuti; in questo modo, con lo stesso significato dei simboli usato nel testo, si ottengono le seguenti
formule:
l
prisma:
St ˆ 2Sb ‡ 2ph
l
piramide retta:
St ˆ Sb ‡ pa
l
tronco di piramide retta:
St ˆ a…p 0 ‡ p† ‡ A ‡ A 0
l
cubo:
l
tetraedro regolare:
l
ottaedro regolare:
l
icosaedro regolare:
l
dodecaedro regolare:
St ˆ 6`2
p
St ˆ 3s2
p
St ˆ 2 3s2
p
St ˆ 5 3s2
q
p
2
St ˆ 3s 25 ‡ 10 5
Le superfici dei solidi di rotazione
Per calcolare la misura della superficie di un cilindro, si considerano le successioni dei prismi inscritti e circoscritti al
cilindro con un numero crescente di facce laterali; tali successioni costituiscono una coppia di classi contigue di cui la
superficie laterale del cilindro eÁ l'elemento separatore.
Analogamente:
l
l
per calcolare la misura della superficie di un cono si considerano le successioni delle piramidi inscritte e circoscritte
al cono con un numero crescente di facce laterali
per calcolare la misura della superficie di una sfera si considera la rotazione attorno al diametro delle poligonali
inscritte e circoscritte ad una semicirconferenza con un numero crescente di lati.
In conseguenza di cioÁ si ottengono le seguenti formule:
l
cilindro:
S` ˆ 2rh
l
cono:
S` ˆ ra
l
tronco di cono:
St ˆ a…r ‡ R† ‡ r 2 ‡ R 2
l
sfera:
St ˆ 4r 2
l
fuso sferico:
S ˆ 2r 2 ( in radianti)
Sb ˆ r 2
Sb ˆ r
Sˆ
2
St ˆ 2r …h ‡ r †
St ˆ r …a ‡ r †
r 2 ( in gradi)
90
Volumi ed equivalenza nello spazio
Il volume di un solido eÁ la caratteristica comune a tutti i solidi che hanno la medesima estensione spaziale; l'unitaÁ di
misura dei volumi eÁ il cubo di lato unitario. Si dimostra che:
l
l
i volumi di parallelepipedi rettangoli che hanno basi congruenti sono proporzionali alle rispettive altezze
il volume di un parallelepipedo rettangolo di dimensioni a, b, c eÁ dato dalla formula V ˆ abc.
Due solidi si dicono equivalenti se hanno la stessa estensione. Il principio di Cavalieri enuncia un criterio per stabilire
se due solidi sono equivalenti:
± se due solidi si possono disporre in modo che risultino equivalenti tutte le loro sezioni con piani paralleli al piano
della base, allora essi sono equivalenti.
18
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
In base a questo principio si dimostra che:
l due prismi sono equivalenti se hanno basi equivalenti ed altezze congruenti
l due piramidi sono equivalenti se hanno basi equivalenti ed altezze congruenti
l una piramide e
Á equivalente alla terza parte di un prisma che ha la base equivalente a quella della piramide e la
stessa altezza
l un cilindro e
Á equivalente a un prisma che ha la base equivalente a quella del cilindro e la stessa altezza
l un cono e
Á equivalente a una piramide che ha la base equivalente a quella del cono e la stessa altezza
l una sfera e
Á equivalente all'anticlessidra.
Misure dei volumi
In base ai teoremi di equivalenza si ricavano le seguenti formule per il calcolo dei volumi:
l
prisma:
V ˆ Sb h
l
piramide:
V ˆ
l
cilindro:
V ˆ r 2 h
l
cono:
V ˆ
l
tronco di piramide:
l
tronco di cono:
V ˆ
1
h …r 2 ‡ R 2 ‡ rR †
3
l
sfera:
V ˆ
4 3
r
3
l
settore sferico:
V ˆ
2 2
r h
3
l
segmento sferico a una base:
V ˆ
1 2
h …3r
3
l
segmento sferico a due basi:
V ˆ
1
1
h r12 ‡ r22 ‡ h3
2
6
l
spicchio sferico:
V ˆ
2 3
r ( in radianti)
3
1
Sb h
3
1 2
r h
3
p
1
V ˆ h B ‡ b ‡ bB
3
V ˆ r 3
Q ISTITUTO ITALIANO EDIZIONI ATLAS
h†
( in gradi)
270
SUPERFICI E VOLUMI
19
Superfici e volumi
MISURE DI SUPERFICI
la teoria eÁ a pag. 2
RICORDA
n Con la convenzione usata nella parte di teoria per i simboli, le superfici dei solidi fondamentali si calcolano applicando le seguenti formule:
Prisma
Piramide
Tronco di piramide
Cilindro
Cono
Tronco di cono
Sfera
S` ˆ 2ph
S` ˆ pa
St ˆ 2ph ‡ 2Sb
0
S` ˆ a …p ‡ p †
S` ˆ 2rh
S` ˆ ra
S` ˆ a …r ‡ R †
S ˆ 4r
2
St ˆ pa ‡ Sb
St ˆ S` ‡ A ‡ A 0
St ˆ 2rh ‡ 2r 2 ˆ 2r …h ‡ r †
St ˆ ra ‡ r 2 ˆ r …a ‡ r †
St ˆ a …r ‡ R † ‡ r 2 ‡ R 2
Comprensione
1 Spiega che cos'eÁ lo sviluppo piano di un solido e descrivi gli sviluppi di un prisma e di una piramide.
2 Enuncia le regole per il calcolo della misura della superficie totale di un prisma e di una piramide, distinguendo il caso in cui il prisma e la piramide sono retti. Spiega poi come si calcola la misura della
diagonale di un parallelepipedo.
3 L'area della superficie laterale di una piramide si trova moltiplicando il semiperimetro di base per la misura dell'apotema. Questa regola eÁ vera:
a. per qualsiasi piramide
b. solo per le piramidi rette
c. solo per le piramidi regolari.
4 Dopo aver spiegato quando un prisma retto eÁ inscritto o circoscritto ad un cilindro, indica quali sono le
caratteristiche delle classi Pi e Pc dei prismi inscritti e circoscritti ad un cilindro e definisci quindi la superficie laterale di un cilindro. Esprimi poi la formula per il calcolo dell'area di tale superficie.
5 Spiega quando una piramide retta eÁ inscritta o circoscritta ad un cono, indica quali sono le caratteristiche
delle classi di queste piramidi e definisci quindi la superficie laterale di un cono. Dai infine la formula per
il calcolo della superficie totale.
6 Dato un arco di circonferenza, spiega che cos'eÁ una poligonale regolare e indica le sue caratteristiche.
Enuncia l'assioma relativo alla superficie di una zona sferica.
7 Dato un arco di circonferenza, considera la classe Si delle superfici che si ottengono facendo ruotare
poligonali regolari inscritte nell'arco attorno ad un diametro della circonferenza e la classe Sc delle su-
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
perfici che si ottengono facendo ruotare poligonali regolari circoscritte; quali sono le caratteristiche di
queste classi? Definisci, di conseguenza, la superficie di una zona sferica.
8 Considera un segmento AB che, ruotando attorno ad una retta r del suo piano che lo interseca al piuÁ in
un estremo, genera una superficie S. Spiega come si calcola l'area di S.
9 Facendo ruotare una poligonale regolare attorno alla retta di un diametro della circonferenza cui si riferisce, in modo che l'asse di rotazione non intersechi la poligonale, si ottiene una superficie S. Enuncia la
regola per il calcolo dell'area di S e dimostrala.
10 Lo sviluppo in un piano di una superficie sferica:
a. daÁ origine a un cerchio
b. daÁ origine a un settore circolare
c. daÁ origine a un rettangolo
d. non si puoÁ realizzare.
11 Enuncia il teorema che permette di calcolare l'area di una zona sferica e deduci da esso la formula per il
calcolo dell'area di una superficie sferica.
12 L'area della superficie di una sfera di raggio r eÁ equivalente:
a. alla superficie totale del cilindro ad essa circoscritto
b. alla superficie laterale del cilindro ad essa circoscritto
c. alle due aree di base del cilindro ad essa circoscritto
d. alla superficie totale del cilindro equilatero in essa inscritto.
13 Il fuso sferico di una sfera di raggio r, il cui diedro ha ampiezza
a. 2r 2
b.
2
r
4
c.
2
r
2
, ha superficie uguale a:
4
d. r 2
Applicazione
Problemi sui poliedri
14 La somma delle tre dimensioni di un parallelepipedo rettangolo eÁ 38a, trova la superficie totale del solido
sapendo che una dimensione eÁ doppia di un'altra ed eÁ anche i 5 della terza.
2
‰880a2 Š
15 L'area della superficie totale di un parallelepipedo rettangolo eÁ 352cm2 ; trova le lunghezze delle sue dimensioni sapendo che una delle dimensioni di base eÁ metaÁ dell'altra e che l'altezza eÁ uguale alla somma
di tali dimensioni.
‰4cm, 8cm, 12cmŠ
16 Un prisma retto ha per base un triangolo equilatero e le sue facce laterali sono equivalenti alla base. Tro-
p
p
va le lunghezze degli spigoli sapendo che l'area della superficie totale eÁ 45 3`2 .
6`, 3 3`
2
17
ESERCIZIO GUIDA
In un parallelepipedo rettangolo gli spigoli di base AB e BC e l'altezza BF sono proporzionali ai numeri 3, 4 e 5 e la loro somma eÁ 60cm;
calcola la misura della superficie totale del solido. Condotto il piano
che passa per due spigoli opposti e incontra le basi lungo una diagonale, calcola la superficie totale di ciascuno dei due prismi che si ottengono.
I dati del problema indicano che: AB : 3 ˆ BC : 4 ˆ BF : 5
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
Applicando la proprietaÁ del comporre otteniamo:
…AB ‡ BC ‡ BF † : …3 ‡ 4 ‡ 5† ˆ AB : 3
!
60 : 12 ˆ AB : 3
!
AB ˆ 15
Utilizzando la stessa proporzione puoi trovare le altre due dimensioni del parallelepipedo.
‰2350cm2 ; 1800cm3 Š
18 L'area della superficie totale di un parallelepipedo rettangolo eÁ 888a2 . Calcola la misura delle sue dimensioni sapendo che sono proporzionali ai numeri 4 , 3 , 16 , trova poi anche la lunghezza della diagonale.
5 5 15
p 12a, 9a, 16a, d ˆ
481a
p
19 In un prisma regolare a base esagonale l'area della superficie totale eÁ 648 3cm2 e di esso si sa che la
superficie laterale eÁ uguale alla somma delle sue superfici di base. Dopo aver trovato le lunghezze dello
spigolo s di base e dell'altezza h del prisma, determina a che distanza dalla base si deve condurre un
piano , parallelo alla base, in modo che la superficie totale di uno dei due prismi che si ottengono
3
p
18 cm _ d ˆ 45 cm
sia i dell'altra.
s
ˆ
6
3
cm,
h
ˆ
9cm,
d
ˆ
4
7
7
20 In un prisma quadrangolare regolare l'area della superficie totale eÁ 264`2 mentre la somma di tutti i suoi
spigoli eÁ 80`. Determina le dimensioni del solido.
22
16
6`, 8`;
3
`,
3
`
21 Una piramide quadrangolare regolare ha lo spigolo di base che eÁ lungo 6`, mentre lo spigolo delle facce
laterali eÁ lungo 9`; calcola la lunghezza dello spigolo s di un cubo che ha la stessa superficie della pi
q
q
ramide e la lunghezza della sua diagonale.
p
p
s ˆ ` 6 2 2 ‡ 1 ; d ˆ 3` 4 2 ‡ 2
22 In una piramide triangolare regolare l'altezza ha la stessa lunghezza dello spigolo di base. Se l'area della
p p
sua superficie totale eÁ di 81 3 13 ‡ 1 cm2 , trova la misura dello spigolo di base s, di quello delle fac
p
p ce laterali s 0 e dell'apotema a della piramide.
s ˆ 18cm, s 0 ˆ 12 3cm, a ˆ 3 39cm
3
dell'altra e l'al4
tezza della piramide cade nel centro del rettangolo; si sa poi che il rapporto fra le aree di due facce lap
3 2
terali consecutive eÁ uguale a
. Trova la lunghezza dell'altezza h della piramide ed esprimi una va5
lutazione, eventualmente approssimata, dell'ampiezza degli angoli che le facce laterali formano con il
p
piano di base.
4
0
00
23 Una piramide ha per base un rettangolo di area 96cm2 le cui dimensioni sono una i
h ˆ 4 2cm; 45 ; arctan
3
53 7 48
24 In una piramide quadrangolare regolare le facce laterali formano un angolo con il piano di base. Se
l'area della superficie totale della piramide eÁ k 2 , calcola, in funzione di k, le lunghezze dello spigolo
di base s, dello spigolo delle facce laterali s 0 , dell'apotema a e dell'altezza h nel caso in cui:
2
3
rq
q
p q
p q
a. ˆ 30
p
p
p
p
k 3
3
k
7
0
2 3 3, a ˆ k
2 3 37
2 3 3, h ˆ
6 a: s ˆ k 2 3 3, s ˆ
b. ˆ 45
6
7
2 3
6
3
6
7
c. ˆ 60
q
q
q
6
7
p p
p p
p
6
6 b: s ˆ h ˆ k
2 1, a ˆ k 2
2
2 1, s 0 ˆ k 3
6
2
2
6
6
p
p
p
4
3
15
3
c: s ˆ
k, s 0 ˆ
k, a ˆ
k, h ˆ k
3
6
3
2
1
7
7
7
7
7
5
25 In un triangolo ABC rettangolo in A, il rapporto fra il cateto AB e la sua proiezione sull'ipotenusa eÁ uguap
le a 3 e l'area del triangolo eÁ uguale a 36 2cm2 . Dal vertice A dell'angolo retto traccia la semiretta per-
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
pendicolare al piano di ABC e prendi su di essa un punto V in modo che sia AV ˆ 6cm. Calcola:
a. le lunghezze degli altri spigoli delle facce laterali della piramide ABCV
p
p p
b. la superficie totale della piramide.
a: 18cm, 6 2cm; b. 18 4 2 ‡ 17 ‡ 1 cm2
26 Una piramide quadrangolare regolare di vertice V ha lo spigolo di base di lunghezza 4a e lo spigolo
p
delle facce laterali di lunghezza 2a 3. Dopo aver calcolato l'ampiezza dell'angolo che ciascuna delle
facce laterali forma con il piano di base, determina a che distanza d da V si deve condurre un piano parallelo a quello di base in modo che il tronco di piramide che si ottiene abbia la superficie laterale
p uguale a quella della piramide staccata dal piano .
45 , d ˆ 2a
27 Sezionando una piramide quadrangolare regolare con un piano passante per il suo vertice e per la diap p
gonale di base si ottiene un triangolo di perimetro 2a 2 ‡ 5 nel quale il rapporto fra il lato obliquo e
p
10
Á
la diagonale di base e uguale a
; calcola:
4
a. l'area della superficie totale della piramide
b. l'ampiezza dell'angolo che ciascuna faccia laterale forma con il piano di base.
12a2 ; 60
28 Una piramide retta a base quadrata ha gli angoli diedri formati dalla base con le facce laterali che sono
ampi 60 e di essa si sa che il lato di base eÁ 24a. Determina a quale distanza dal vertice occorre condurre
un piano parallelo alla base in modo che la superficie laterale della piramide che si stacca sia uguale a
p quella del tronco di piramide che si viene a formare.
distanza del vertice dal piano ˆ 6a 6
29 In un tronco di piramide quadrangolare regolare gli spigoli delle due basi sono uno il triplo dell'altro; si
sa inoltre che le facce laterali formano angoli diedri di ampiezza 60 con il piano della base maggiore.
p Qual eÁ l'altezza del tronco se la sua superficie totale eÁ 416`2 ?
4 3`
30 Un solido eÁ formato da un prisma regolare a base triangolare e da due piramidi regolari, aventi ciascuna
la base coincidente con una base del prisma, con il vertice rivolto verso l'interno del prisma. L'altezza di
ciascuna piramide eÁ uguale al lato di base e l'altezza del prisma eÁ quattro volte il lato di base. Determina:
lo spigolo di base del prisma, la sua altezza e l'apotema di ciascuna delle due piramidi sapendo che la
"
p
r #
superficie totale del solido eÁ 8 24 ‡ 39 `2 .
13
4`; 16`, 2
3
`
31 In una piramide quadrangolare regolare di vertice V il diedro che la faccia laterale forma con il piano
della base eÁ di 60 ; si sa inoltre che la distanza del centro della base da ciascuna delle facce laterali misura 12a. Calcola l'area della superficie totale della piramide.
Il piano passante per V e per la diagonale di base e un piano parallelo alla base stessa e posto a distanza
x da V individuano un tronco di piramide; esprimi in funzione di x la sua superficie totale e determina
p
‰S ˆ 2304a2 ; x ˆ 6aŠ
poi il valore di x per il quale tale superficie vale 1128 ‡ 180 6 a2 .
Problemi sui solidi di rotazione
32 Siano O e O 0 i centri delle due circonferenze di base di un cilindro di raggio r e altezza 4r; determina la
posizione di un punto V sul segmento OO 0 in modo che i due coni di vertice V e basi coincidenti con le
p
‰OV ˆ r _ OV ˆ 3r Š
basi del cilindro abbiano le superfici laterali che stanno nel rapporto 5.
33 L'altezza di un cono circolare retto eÁ la metaÁ dell'apotema di lunghezza a; calcola, in funzione di a, la
1
misura della superficie totale del cono e quella del cilindro in esso inscritto che ha altezza pari ad di
3
quella del cono.
h
p 2
pi
2
4
Q ISTITUTO ITALIANO EDIZIONI ATLAS
a 3‡2 3 ;
9
a 6‡
SUPERFICI E VOLUMI
3
3
di quella della superficie di base; trova le lunghezze
2
dell'apotema e dell'altezza in funzione del raggio di base r. Calcola poi il rapporto fra la superficie del
cubo il cui spigolo eÁ uguale all'apotema del cono e la superficie totale del cono stesso.
34 L'area della superficie laterale di un cono retto eÁ i
p
5
3
27
r;
a ˆ r; h ˆ
2
2
5
35 In un tronco di cono, il raggio della base maggiore B eÁ il doppio di quello della base minore B 0 . Il cono
avente per base B 0 e vertice nel centro di B ha superficie laterale di area 30cm2 . Quanto misura l'area
della superficie laterale del tronco? Con questi dati eÁ possibile valutarne la superficie totale?
‰S` ˆ 90cm2 ; noŠ
36 L'apotema di un cono di vertice V eÁ lungo 30cm e la sua altezza eÁ i 4 del raggio di base; determina a
3
quale distanza da V si deve condurre un piano parallelo alla base del cono in modo che il cilindro in
esso inscritto e avente per base il cerchio sezione abbia superficie laterale uguale a 162cm2 .
‰18cm _ 6cmŠ
37 Un piano parallelo alla base di un cono retto individua un tronco di cono di cui si sa che l'area della
superficie laterale eÁ uguale a 14`2 e l'area della superficie totale eÁ 32`2 . Calcola le lunghezze del raggio di base del cono e del suo apotema sapendo che il rapporto fra i raggi delle due basi del tronco eÁ
p
p
3
r ˆ 12 ` 2, a ˆ 20 ` 2
uguale a .
5
3
4
38 Un solido eÁ formato da un cilindro sormontato da un cono di vertice V avente la base coincidente con
quella del cilindro; la generatrice AB del cilindro e quella VB del cono hanno la stessa lunghezza ` e
l'angolo formato dalle due generatrici eÁ di 120 ; calcola:
a. la superficie totale del solido;
b. considerato il triangolo ABV ed il solido S che si ottiene dalla sua rotazione completa attorno alla
retta AB, calcola la superficie totale di S.
p
p
a: `2 3 ‡ 3
4 2
3 ; b: 1 `2
2
3‡3
39 Lo sviluppo su un piano della superficie laterale di un cono retto daÁ luogo ad un semicerchio di raggio
2`; determina il raggio di base r del cono, deduci le sue caratteristiche e trova l'area della sua superficie
totale. Sezionando il cono con un piano parallelo al piano di base si ottiene un cerchio di raggio x; determina il valore di x in modo che la superficie laterale del cono staccato da tale piano sia media pro
porzionale fra le due aree di base del tronco di cono rimanente.
`
r ˆ `; St ˆ 3`2 ; x ˆ
2
40 Un cono retto ha il raggio di base di lunghezza 6` e l'altezza di lunghezza 8`; trova:
a. l'area della superficie della sfera in esso inscritta,
b. il raggio del cerchio individuato dai punti di tangenza della sfera con la superficie laterale del cono
c. la superficie laterale del tronco di cono che ha per basi la base del cono e il cerchio individuato al
punto precedente.
12
252 2
2
a: 36` ; b:
5
`; c:
5
`
41 La sezione di una sfera di raggio r con un piano daÁ origine ad una calotta la cui superficie eÁ uguale alla
superficie laterale del cono retto che ha per base il cerchio sezione e per vertice l'estremo del diametro
perpendicolare al piano secante e situato da parte opposta rispetto alla calotta. Determina la distanza del
p
piano secante dal centro della sfera.
5 2 r
p
42 Un trapezio isoscele ABCD avente la base maggiore AB lunga 26 2cm eÁ circoscritto ad un semicerchio
p
di centro O e raggio r ˆ 12 2cm. Determina la superficie totale del solido che si ottiene facendo ruo‰1392cm2 Š
tare il trapezio di una rotazione completa attorno alla retta del diametro.
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
MISURE DI VOLUMI
la teoria eÁ a pag. 10
RICORDA
n Con la convenzione per i simboli usata nella parte di teoria, i volumi dei solidi fondamentali si calcolano
applicando le seguenti formule:
Prisma
V ˆ Sb h
Piramide
V ˆ
1
Sb h
3
Tronco di piramide
V ˆ
p
1
h B ‡ b ‡ bB
3
Cilindro
V ˆ r 2 h
Cono
V ˆ
1 2
r h
3
Tronco di cono
V ˆ
1
h…r 2 ‡ R 2 ‡ rR †
3
Sfera
V ˆ
4 3
r
3
Comprensione
43 Considera l'insieme dei parallelepipedi rettangoli aventi basi congruenti; che cosa si puoÁ dire di essi?
Giustifica la tua risposta.
44 Enuncia e dimostra il teorema che consente di determinare il volume di un parallelepipedo rettangolo.
45 Dopo aver detto che cosa significa che due solidi sono equivalenti, enuncia il principio di Cavalieri.
46 Un prisma eÁ equivalente a:
a. un parallelepipedo che ha la base equivalente a quella del prisma e la stessa altezza
b. una piramide che ha la stessa base del prisma e altezza tripla
c. un qualsiasi altro prisma che ha la stessa altezza
d. al doppio di una piramide che ha la base equivalente a quella del prisma e la stessa altezza
e. un cilindro che ha la base equivalente a quella del prisma e la stessa altezza
f. alla terza parte di un cono che ha base equivalente a quella del prisma e la stessa altezza.
V
F
V
F
V
F
V
F
V
F
V
F
47 Completa gli enunciati dei seguenti teoremi e dimostrali.
a. Due prismi sono equivalenti se .....................
b. Due piramidi sono equivalenti se ..................
c. Una piramide eÁ equivalente ad un prisma se ........................
48 Completa gli enunciati dei seguenti teoremi e, utilizzando il principio di Cavalieri e sulla falsariga delle
dimostrazioni che hai visto nella parte teorica, dimostra che:
a. un cilindro ed un prisma sono equivalenti se ....................
b. un cono ed una piramide sono equivalenti se ...................
49 Il volume di una sfera eÁ equivalente a quello del solido che si ottiene:
a. togliendo da un cubo con lo spigolo uguale al diametro della sfera due piramidi aventi per basi due
facce opposte e per altezze metaÁ dello spigolo del cubo
b. togliendo da un cilindro con il raggio di base uguale a quello della sfera due coni aventi per basi le
basi del cilindro e per altezza la metaÁ dell'altezza del cilindro
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
c. togliendo da un cilindro equilatero, avente come raggio di base il raggio della sfera, due coni aventi
per basi le basi del cilindro e per altezza un segmento congruente al raggio di base del cilindro
d. togliendo da un cilindro, avente come raggio di base il raggio della sfera, due coni aventi per basi le
basi del cilindro e per altezza un segmento congruente al raggio di base del cilindro.
50 In una sfera di raggio R, VT e VS sono i volumi di due spicchi sferici T ed S i cui diedri hanno ampiezza,
in radianti, e ; il rapporto fra VT e VS eÁ uguale a:
c.
r
d. nessuno dei precedenti valori
a.
b.
Applicazione
Problemi sui poliedri
51 La diagonale di un cubo misura d ; esprimi la misura della superficie totale e del volumedel cubo in
p 3
funzione di d.
3d
2
2d ;
9
52 Un prisma retto ha per base un triangolo rettangolo i cui cateti misurano 5cm e 12cm e la sua altezza eÁ
congruente all'ipotenusa del triangolo di base. Calcola la misura della superficie totale ed il volume del
solido.
‰450cm2 ; 390cm3 Š
53 L'area della superficie totale di un parallelepipedo rettangolo eÁ 5440a2 e le sue dimensioni sono proporzionali ai numeri 10, 5, 8. Calcola la misura del volume e della diagonale.
(Suggerimento: indica con 10x, 5x, 8x le dimensioni del parallelepipedo, calcola l'espressione della su
p perficie totale e imponi che sia uguale al valore dato)
25600a 3 ; 12 21a
2
54 L'area della superficie totale di un parallelepipedo rettangolo eÁ 246dm e la sua altezza eÁ 3dm; le dimen‰216dm3 Š
sioni del rettangolo di base differiscono di 1dm. Calcola il volume del solido.
55 Un parallelepipedo rettangolo ha per base un quadrato di lato ` ; se la diagonale del parallelepipedo mih
p
p 3 i
sura 2`, calcola la superficie totale ed il volume del solido.
2
S ˆ 2` 1 ‡ 2 2 ; V ˆ
2`
3
56 Un prisma retto ha per base un triangolo equilatero e l'altezza del prisma eÁ i del lato di base; se il
4
p
volume del solido eÁ 12 3 cm3 , calcola le misure dei suoi spigoli e quella dell'area della superficie toh
p 2 i
tale.
lato di base ˆ 4cm; altezza ˆ 3cm; S ˆ 36 ‡ 8 3 cm
p
57 Un parallelepipedo retto ha per base un rombo ed ha il volume di 1536 3cm3 ; la diagonale maggiore
del parallelepipedo eÁ lunga 32cm e forma un angolo di 60 con il piano di base. Calcola la superficie
p
totale del solido.
192 ‡ 640 3 cm2
p
58 Un prisma regolare a base esagonale ha la superficie totale pari a 72 3m2 e la sua superficie laterale eÁ
‰72m3 Š
uguale a quella di una base. Calcola il volume del solido.
59 Il volume di un parallelepipedo a base quadrata eÁ 3456cm3 e di esso si sa che l'altezza eÁ doppia dello
spigolo di base. Un piano inclinato di 30 rispetto al piano di base, in modo che il poligono sezione sia
p
4 ‡ p3
 . Calcola le superfici totali dei
un rettangolo, lo divide in due solidi i cui volumi hanno rapporto
i
8
3 h
p
due solidi che si ottengono.
528 ‡ 192 3 cm2 ; 912cm2
60 Una piramide triangolare regolare ha lo spigolo di base che misura 12 cm. Sapendo che l'altezza della
piramide eÁ la metaÁ dell'apotema, calcola l'area della superficie totale ed il volume del solido.
h
i
p
p
S ˆ 72 ‡ 36 3 cm2 ; V ˆ 24 3cm3
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
61 Una piramide triangolare regolare ha l'altezza congruente allo spigolo di base e la sua superficie totale eÁ
p
p
9 3 1 ‡ 13 cm2 . Calcola la misura dello spigolo di base ed il volume della piramide.
p
spigolo ˆ 6cm; V ˆ 18 3cm3
62 Sia ABC un triangolo equilatero di lato ` ; traccia per il vertice B la retta perpendicolare al piano del triangolo e prendi su di essa un punto V in modo che l'angolo VAB sia di 30 . Calcola il volume e l'area della
superficie totale della piramide che si ottiene congiungendo V con i vertici del triangolo.
63
Sˆ
ESERCIZIO GUIDA
p
7 ‡p13 2
` ; V ˆ 1 `3
12
4 3
Una piramide ha altezza h; determina a quale distanza dal vertice deve essere condotto un piano parallelo alla base in modo che le due parti in cui resta divisa la piramide siano equivalenti.
La piramide data P e quella P 0 staccata dal piano si corrispondono in una omotetia di centro V ; indicando con x l'altezza della
x
piramide P 0 , il rapporto di omotetia eÁ . Inoltre le aree delle basi
h
stanno fa loro come i quadrati delle rispettive altezze.
Indicando con b e b 0 le aree delle due basi, puoi quindi scrivere la
proporzione b : b 0 ˆ h2 : x 2 dalla quale ricavi che b 0 ˆ ::::::::::::::
Puoi adesso calcolare la misura del volume della piramide P 0 e del
tronco di piramide restante e imporre che i due solidi siano equi
valenti.
h

xˆ p
3
2
10
dell'apotema e la differenza tra la superficie
13
‰V ˆ 400a3 Š
laterale e quella di base eÁ 160a 2 . Calcola il volume della piramide.
64 In una piramide quadrangolare regolare il lato di base eÁ
65 Un cubo eÁ diviso in due parti da un piano passante per la diagonale di tre facce aventi un vertice in comune. Calcola l'area della superficie totale ed il volume della piramide triangolare cosõÁ ottenuta in fun
p
zione dello spigolo ` del cubo.
1 3
1 2
V ˆ
6
`;Sˆ
2
` 3‡
3
66 Tenendo presente che se in una piramide a base quadrata uno spigolo eÁ perpendicolare al piano della
base le sue facce sono triangoli rettangoli, calcola il volume della piramide sapendo che il lato di base eÁ
p
` e che la sua superficie totale eÁ 3 ‡ 5 ` 2 .
V ˆ 2 `3
3
67 Di un tronco di piramide a base quadrata si sa che la somma delle aree di base misura 500a2 ; un piano
passante per due spigoli laterali opposti taglia il tronco individuando un trapezio isoscele che ha il lato
p
obliquo lungo 20a e l'altezza lunga 10 3a. Calcola la misura del volume del tronco di piramide.
p
6500 3 3
a
3
p
68 In una piramide esagonale regolare la superficie totale eÁ 162 3a2 e ogni faccia forma un angolo di 60
col piano di base. Calcola il volume della piramide. Un piano parallelo alla base e a distanza x dal verp
tice individua un esagono regolare di area 6 3a2 . Calcola il volume del prisma inscritto nella piramide
che ha per basi il poligono sezione e la sua proiezione ortogonale sulla base della piramide.
p
p 162 3a3 ; 36 3a3
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
69 Un oggetto ha la forma di un cubo di lato ` con un foro a forma di piramide avente la base coincidente
con quella del cubo e vertice nel suo centro. Calcola il volume del solido e la sua superficie totale.
p
V ˆ 5 `3 ; St ˆ 5 ‡ 2 `2
6
70 Un parallelogramma ABCD eÁ la base di un parallelepipedo retto; sia P il punto del lato AB tale che
AP  2PB. Sia il piano passante per PC e perpendicolare al piano del parallelogramma. Calcola il rapporto fra i volumi dei due solidi in cui il parallelepipedo resta diviso da .
(Suggerimento: assegna delle lunghezze arbitrarie allo spigolo AB, all'altezza del parallelogramma e all'altezza del prisma)
‰5Š
Problemi sui solidi di rotazione
71 L'angolo di apertura di un cono eÁ 60 ed il suo apotema eÁ lungo 12cm. Calcola la superficie totale del
4
cono e quella del cilindro in esso inscritto che ha volume pari a di quello del cono.
9
h
i
p
St …cono† ˆ 108cm2 ; St …cilindro† ˆ 16 2 ‡
3 cm2
72 La sezione di un cilindro con un piano passante per il suo asse ha area 80cm2 ; si sa inoltre che il rapporto
5
fra l'altezza ed il raggio del cilindro eÁ . Calcola la superficie totale ed il volume del cilindro.
2
2
3
‰S ˆ 112cm ; V ˆ 160cm Š
73 Un cilindro retto ha la superficie laterale che misura 108cm2 e il rapporto fra la sua altezza e il raggio di
base eÁ 6. Un prisma retto eÁ circoscritto al cilindro ed ha per base il triangolo equilatero circoscritto alla
circonferenza di base del cilindro. Trova la misura del volume del prisma svuotato del volume del cilin
p
dro.
162 3 3 cm3
17
e l'area di base eÁ 25cm2 .
74 Il rapporto fra l'area della superficie totale e quella laterale di un cilindro eÁ
12
Calcola il volume del cilindro.
‰V ˆ 300cm3 Š
75 L'altezza di un cono circolare retto eÁ doppia del raggio r di una sfera ed i due solidi sono equivalenti.
Calcola la misura del raggio di base del cono e quella della sua superficie totale.
h
p
pi
raggio ˆ r 2; S ˆ 2r 2 1 ‡ 3
76 Un solido eÁ formato da un cilindro equilatero e da un cono retto, avente la base coincidente con una
delle basi del cilindro, che ne costituisce una cavitaÁ. Se la superficie totale del solido eÁ 400a2 e se l'al3
‰896a3 Š
tezza del cono eÁ i di quella del cilindro, qual eÁ il volume?
8
77 Lo sviluppo piano di un cono circolare retto eÁ un settore circolare di raggio r e ampiezza 60 . Trova il
p
volume del cono.
35 3
r
V ˆ
648
78 Un cono circolare retto ha la superficie laterale che eÁ doppia della superficie di base e la sua altezza
p
misura 6 3cm. Dopo aver dimostrato che il cono eÁ equilatero, calcola la sua superficie totale ed il
p
suo volume.
S ˆ 108cm2 ; V ˆ 72 3cm3
79 Lo sviluppo piano della superficie laterale di un cono circolare retto di vertice V e avente raggio di base r
daÁ origine ad un semicerchio; calcola la misura della superficie totale del cono. Determina poi un punto
P sull'altezza VO del cono in modo che il cilindro di altezza PO e base coincidente con quella del cono
h
i
abbia superficie totale uguale a quella del cono.
St…cono† ˆ 3r 2 ; PO ˆ r
2
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
80 Un tronco di cono ha i raggi delle basi che misurano rispettivamente 40cm e 10cm mentre l'apotema
misura 50cm. Calcola l'area della superficie totale e il volume:
a. del tronco;
b. del cono da cui il tronco proviene.
a: St ˆ 4200cm2 , V ˆ 28000cm3 ; b: St ˆ 12800 cm2 , V ˆ 256 103 cm3
3
9
81 La lunghezza del meridiano terrestre eÁ circa 40000km; trova l'area della superficie ed il volume della
Terra.
16 1014 2
32 1021 3
14 2
21 3
Sˆ
m 5,093 10 m ; V ˆ
3
2
m ˆ 1,081 10 m
64
3
82 La differenza fra i volumi di due sfere eÁ
cm3 ed il rapporto fra i raggi eÁ . Calcola l'area della su3
5
perficie delle due sfere.
400
144
 ; S2 ˆ p
 S1 ˆ p
737
737
83 Un cono circolare retto ha la base coincidente con quella di una semisfera ed eÁ situato nel semispazio
opposto a quello della semisfera; inoltre si sa che le generatrici del cono formano un angolo di 60 con il
piano della base. Un piano passante per l'asse del cono determina una superficie sezione di area
p
‡2 3
rispetto ad una certa unitaÁ di misura u2 . Calcola il volume del solido e quello del cilindro
32
h
p i
2 ‡ p
3 u3 ; 1 ‡ 3 u3
ad esso circoscritto.
192
64
84 Un cono circolare retto eÁ generato dalla rotazione completa di un triangolo rettangolo di area 96cm2
attorno ad un cateto; il volume del cono eÁ 1024cm3 . Calcola l'area della sua superficie laterale.
‰r ˆ 16cm; h ˆ 12cm; S` ˆ 320cm2 Š
85 Un piano taglia una sfera lungo una circonferenza di raggio 3a e
divide il diametro della sfera ad esso perpendicolare in parti proporzionali a 4 e 9. Calcola l'area della superficie delle due calotte e il
loro volume.
117 2
31 3
567 3
2
S1 ˆ 13a ; S2 ˆ
4
a ; V1 ˆ
3
a ; V2 ˆ
16
a
86 Un cono di vertice V eÁ inscritto in una semisfera di raggio r e la sua
base coincide con quella della semisfera. Un piano parallelo alla
base e posto a distanza x da V interseca la sfera ed il cono individuando una corona circolare. Determina il valore di x in modo che
il rapporto fra l'area della corona circolare e quella del cerchio di
p 1
2 2
r
base del cono sia uguale a .
4
4
87 Sono dati una sfera di raggio r, il cilindro equilatero ed il cono equilatero in essa inscritti. Verifica che il
volume del cilindro eÁ medio proporzionale fra il volume del cono e quello della sfera.
88 EÁ dato un cono di raggio r ed altezza 3r ; inscrivi in esso un cilindro che abbia l'area della superficie
totale uguale a 2 volte l'area di base del cono.
1
raggio del cilindro
2
r
89 Un cono ha l'altezza congruente al raggio di base di misura a. Determina la lunghezza del segmento di
cui si deve diminuire l'altezza ed aumentare il raggio di base in modo che il cono ottenuto sia equivalente a quello dato; calcola poi le aree delle superfici totali dei due solidi e stabilisci quale dei due ha
area maggiore.
1 p
2
a
5
1 ; il secondo
90 In un trapezio la base maggiore eÁ il doppio di quella minore. Considera i due solidi che si ottengono
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
facendo ruotare il trapezio prima intorno alla base maggiore e poi intorno alla base minore. Dire se eÁ
possibile calcolare il rapporto fra i volumi dei due solidi e, in caso affermativo, dare una sua valutazione.
4
5
91 Sia P un punto del lato AD ˆ 1 di un quadrato ABCD. Determina la posizione di P in modo che sia
uguale a 17 il rapporto fra le aree delle superfici dei solidi che si ottengono facendo ruotare il quadri11
latero PDCB di una rotazione completa prima attorno alla retta del lato AD e poi attorno alla retta del
lato BC.
3
AP ˆ
4
Problemi da risolvere per via trigonometrica
92 Un parallelepipedo rettangolo ha base quadrata; determina l'ampiezza dell'angolo x che la diagonale
forma con il piano di base sapendo che il rapporto fra il suo volume e quello di un cono circolare retto
p
h
i
9 2 12
.
xˆ
che ha semiapertura x e raggio di base congruente al lato del quadrato eÁ
8
d ˆ 2x, determina
93 Una piramide regolare ha vertice V e per base un esagono di lato AB ˆ 2`, posto AVB
h
i
il valore di x sapendo che l'area totale eÁ doppia di quella laterale.
xˆ
6
94 Sia 2x l'ampiezza dell'angolo al vertice A di un triangolo isoscele ABC di base BC e lato obliquo AB ˆ `;
sia il solido che si ottiene facendo ruotare il triangolo attorno alla retta del lato AC. Dopo aver osservato che eÁ formato da due coni aventi la base in comune, determina l'ampiezza degli angoli del triangolo in modo che il rapporto fra le superfici laterali del cono di vertice A e del cono di vertice C sia
p p
6‡ 2
uguale a
.
‰30 , 75 , 75 Š
2
95 In un triangolo ABC rettangolo in B il cateto AB eÁ lungo 4cm. Determina l'ampiezza dell'angolo di vertice A in modo tale che il volume del solido che si ottiene facendo ruotare il triangolo di una rotazione
completa attorno ad una retta parallela al lato BC e a distanza 3cm da esso sia uguale a
p 3
208
‰15 Š
2
3 cm .
3
96 In un trapezio ABCD, rettangolo in A e B, la diagonale AC eÁ perpendicolare al lato obliquo CD. Determina
d in modo che la superficie laterale del tronco di cono che si ottiene facendo
l'ampiezza dell'angolo CAD
p
5 3 2
` , essendo `
ruotare il trapezio di una rotazione completa attorno alla retta del lato AB sia uguale a
8
la lunghezza della base maggiore AD.
p p
d ˆ 60 _ CAD
d ˆ arcsin
CAD
23
3
4
50
97 Dato un ottaedro regolare di lato ` come in figura, sia P un punto del
lato FC. Considerata la piramide APCB, determina l'ampiezza dell'an
p p
2 3 1 3
d
`.
golo PAC in modo tale che il suo volume sia uguale a
12
h i
6
98 Un parallelepipedo a base rettangolare ABCD eÁ tale che una faccia laterale forma con il piano di base un diedro di ampiezza x e lo spigolo
laterale eÁ lungo quanto la dimensione maggiore del rettangolo. La somma delle dimensioni del rettangolo di base eÁ 16dm e una dimensione eÁ
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
5
dell'altra. Determina l'ampiezza dell'angolo x in modo tale che il volume del parallelepipedo sia
3
p 3
‰45 Š
uguale a 300 2dm .
p
99 In un parallelogramma ABCD di area 36 3`2 , il lato AB eÁ doppio del lato BC e la diagonale BD eÁ perpendicolare al lato AD. Un parallelepipedo retto ha per base il parallelogramma e per altezza un segmento congruente al lato AD; preso un punto P sullo spigolo BF, determina l'ampiezza dell'angolo
p 2
d in modo che sia verificata la relazione PD 2 ‡ AP 2 ‡ AD 2 ˆ 1152 2
‰15 Š
3 `.
PAB
i
100 Una piramide retta ha per base un triangolo isoscele ABC rettangolo in B con l'ipotenusa AC lunga 4cm.
Detto O il centro della circonferenza inscritta nel triangolo e indicato con V il vertice della piramide, sia
d in modo che
P un punto appartenente all'altezza della piramide. Determina l'ampiezza dell'angolo PBO
p

p

‰30 Š
6 cm3 .
la piramide di base ABC e vertice P abbia volume uguale a 8 2 3
9
101 La diagonale BD ˆ 8` di un rettangolo ABCD forma un angolo di 30 con il lato AB; tale rettangolo eÁ la
base di una piramide avente il vertice V sulla retta perpendicolare al piano del rettangolo passante per il
punto medio del lato AD. Determina l'inclinazione del piano VBC rispetto a quello del rettangolo in
modo che il rapporto fra la somma delle aree delle facce opposte VAD e VBC e la somma delle aree
p
hi
15
.
delle altre due facce sia uguale a
6
5
p
102 Nel triangolo acutangolo ABC, i lati AB e BC misurano rispettivamente ` e 2`. Detto H il piede deld in modo tale che la differenza fra
l'altezza relativa al lato AB, determina l'ampiezza dell'angolo ABC
i volumi dei solidi generati dalla rotazione completa dei triangoli BCH e ACH attorno alla retta del lato
AB sia uguale a
hi
1 3
` .
3
4
PROBLEMI RIASSUNTIVI
103 Un triangolo isoscele ABC rettangolo in C ha l'ipotenusa AB lunga 10cm. Determina un punto P sul lato
AC in modo tale che il volume del solido generato dal triangolo ABP in una rotazione completa attorno
p 40
cm2 .
al lato AB sia uguale a
AP ˆ 2 2cm
3
104 Un prisma retto ha per base un triangolo equilatero ABC di lato 2cm e per altezza un segmento lungo
5cm; un piano parallelo alla faccia di lato AB taglia il triangolo di base lungo un segmento PQ. Determina come deve essere condotto il piano in modo che i due prismi in cui rimane diviso quello dato siano
p equivalenti.
PC ˆ 2cm
105 Un trapezio isoscele di area 20cm2 eÁ circoscritto a una circonferenza; facendo ruotare di mezzo giro
entrambe le figure attorno alla retta del diametro perpendicolare alle basi del trapezio si ottiene una sfera
21
, calcola le
inscritta in un tronco di cono. Se il rapporto fra il volume del tronco e quello della sfera eÁ
8
lunghezze dei lati del trapezio e il raggio della circonferenza.
‰2cm, 8cm, 5cm; raggio ˆ 2cmŠ
106 In un trapezio rettangolo ABCD appartenente ad un piano , la base maggiore AB, la base minore CD e
l'altezza AD sono lunghe rispettivamente 10cm, 2cm e 6cm. Sia V un punto della perpendicolare al piano condotta dal punto medio del lato AD del trapezio; considerata la piramide di vertice V e avente
per base il trapezio, sia un piano che dista 6cm dal piano . Indicato con x l'angolo che forma con il
piano a cui appartiene la faccia CBV , determina x affinche la somma delle aree delle due basi del tronco
p
‰30 _ 75 Š
di piramide che si viene a formare sia uguale a 36 5 2 3 cm2 .
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
107 Un rettangolo ABCD ha il perimetro lungo 20`; facendolo ruotare di una rotazione completa prima attorno alla retta del lato AB e poi attorno alla retta del lato BC si ottengono due cilindri la cui somma eÁ
p
5 `; 15 `
equivalente a una sfera di raggio 5 3 9`. Trova le lunghezze dei lati del rettangolo.
2
2
2
108 In una sfera di raggio r eÁ inscritto un cilindro. Determina l'angolo di semiapertura del cono che ha per
base la base del cilindro e per vertice il centro della sfera in modo tale che il cilindro abbia superficie
p
3 2 p
‰60 Š
r
3‡2 .
totale uguale a
2
109 Sia AC una corda di una semicirconferenza di diametro AB ˆ 2r; sia D il punto d'intersezione della semicirconferenza con la retta parallela ad AB condotta da C e siano H e K le proiezioni dei punti D e C
sul diametro AB. Considera i due solidi V1 e V2 che si ottengono facendo ruotare il rettangolo CDHK e il
triangolo ACH di una rotazione completa attorno alla retta del diametro AB; determina l'ampiezza deld in modo che:
l'angolo CAB
a. i due solidi siano equivalenti;
b. il rapporto fra le aree delle superfici laterali di V1 e V2 sia uguale a 2.
"
#
r
3
; b:
a: x ˆ arcsin
7
3
110 Un cono di vertice V ha l'altezza VO congruente al raggio di base AO ed entrambi i segmenti sono
lunghi 8cm; determina a che distanza d da V deve essere condotto un piano parallelo allapbase
in

modo che il tronco di cono che si viene ad individuare abbia superficie laterale uguale a 28 2cm2 .
Verificato che cioÁ si ottiene per d ˆ 6, in tale situazione:
a. trova l'area della superficie della sfera inscritta nel cono piuÁ piccolo che il piano stacca da quello
dato;
b. considerato il trapezio isoscele, sezione del tronco di cono individuato da , con un piano perpendicolare al piano di base e passante per l'asse del cono, determina l'area della superficie del solido
che si ottiene facendo ruotare tale poligono di una rotazione completa attorno alla retta della base
p
p
minore.
a: 144 3 2 2 ; b: 8 8 ‡ 2
111 Un triangolo ABC rettangolo in A ha l'angolo di vertice B che misura 60 e l'ipotenusa BC di lunghezza
2a. Sia r una retta passante per A che non interseca il triangolo e siano H e K rispettivamente le proied in modo che il solido che si ottiene
zioni dei vertici B e C su r; determina l'ampiezza dell'angolo BAH
p
hi
2 3 3
a .
facendo ruotare ABC di una rotazione completa attorno a r abbia volume
6
3
112 Una sfera di centro O e raggio unitario eÁ tagliata da un piano che dista x dal centro O; sia C la maggiore delle due calotte che si vengono a formare e sia C 0 il cono avente per base il cerchio sezione e tale
che le sue generatrici siano tangenti alla sfera. Esprimi in funzione di x l'area della superficie del solido
che si ottiene dall'unione di C e C 0 e determina poi a quale distanza da O deve essere condotto il piano
16
di quella del cerchio massimo della sfera.
in modo che tale area sia uguale ai
xˆ1
3
3
113 Un tronco di cono ha la base minore di raggio HA ˆ 6`, la base maggiore di raggio KB ˆ 2HA e l'altezza
HK congruente al diametro della base minore; siano poi C e C 0 i due coni aventi per basi rispettivamente
la base minore e la base maggiore del tronco e vertice V sul segmento HK . Determina la posizione del
p
5
R,
punto V in modo che il rapporto fra le aree delle superfici laterali dei coni C e C 0 sia uguale a
12
essendo R il rapporto fra l'area della superficie laterale del tronco e la somma delle aree delle sue basi.
‰HV ˆ 4`Š
d ˆ x con x
114 Data una semicirconferenza di diametro AB ˆ 2r e centro O, sia AP l'arco per il quale AOP
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
acuto. Condotta da P la tangente alla semicirconferenza che incontra in Q il prolungamento del diametro AB, considera i due solidi ottenuti da una rotazione completa del triangolo QPB attorno alla retta QB
e attorno alla retta PB. Determina il valore di x in modo tale che il rapporto tra i volumi dei due solidi sia
p
3
‰60 Š
.
uguale a
3
115 E' data una piramide regolare retta a base quadrata ABCD di lato `; determina l'ampiezza dell'angolo x
che lo spigolo AV forma con la diagonale di base AC in modo tale che, detto V1 il volume della piramide
e V2 il volume del solido generato dal triangolo ABC in una rotazione completa attorno alla retta AC, sia
p
2 3…
‰45 Š
` 1 ‡ †.
verificata la relazione V1 ‡ V2 ˆ
6
116 Un parallelepipedo di altezza 9cm ha base quadrata ABCD di lato 4cm; sia P un punto appartenente
1
allo spigolo laterale AE tale che PA ˆ AE e sia Q un punto dello spigolo laterale DH tale che PQ
3
sia parallelo ad AD. Conduci per PQ un piano che interseca il parallelepipedo e che forma un angolo
di 30 con il piano contenente la base ABCD. Determina i volumi dei due solidi in cui il parallelepipedo
d in
resta diviso da tale piano. Preso poi un punto T sul segmento PQ, trova l'ampiezza x dell'angolo TAP
modo tale che la superficie del solido generato dalla rotazione del triangolo PAT attorno alla retta TA sia
p
9 2
16 9 2p
16 18 2p
.
uguale a
3
;
V
3
;
45
ˆ
V
ˆ
2
1
2
3
3
117 Sia l'ampiezza dell'angolo al centro corrispondente ad una corda AB di una circonferenza di centro O e
raggio r e sia S il segmento circolare corrispondente che contiene il centro O. Trova l'ampiezza di in modo che il segmento sferico a una base generato dalla rotazione di S attorno alla retta perpendicolare ad AB e
p
1
r 3 16 9 3 . Per tale valore di ,
passante per il centro della circonferenza abbia volume uguale a
24
determina poi il volume e la superficie totale del solido che si ottiene da una rotazione completa del trian
p 2
golo ABO attorno alla retta del diametro parallelo alla corda AB.
1 3
60 ; V ˆ
2
r ; St ˆ 2 3r
118 Data una semicirconferenza di centro O e diametro AB ˆ 2r, sia t la tangente alla semicirconferenza in
B. Determina un punto P sulla semicirconferenza in modo tale che, detta H la proiezione di P su t, sia
V
4
verificata la relazione 1 ˆ , essendo V1 il volume del solido generato dal trapezio OBHP in una ro5
V2
tazione completa attorno alla retta OB e V2 il volume del solido generato dallo stesso trapezio in una
rotazione completa attorno alla retta PH.
d ˆ 60
ABP
119 In un triangolo ABC i lati AB e AC sono lunghi rispettivamente 5cm e 6cm mentre il coseno dell'angolo
3
di vertice A eÁ uguale a . Dopo aver calcolato il perimetro e l'area del triangolo, traccia da B una se5
d in modo che il rapporto tra i
miretta che incontra in P il lato AC; determina l'ampiezza dell'angolo PBC
volumi dei due solidi generati dai due triangoli ABP e CBP in una rotazione completa attorno alla retta
AC sia uguale a
17
.
25
‰2p ˆ 16cm; area ˆ 12cm2 ; 45 Š
120 Dato un triangolo equilatero ABC di lato `, si considera una retta r passante per A esterna al triangolo e
che forma un angolo di 30 con il lato AB e una retta s anch'essa passante per A ed esterna al triangolo
che forma un angolo di 60 con il lato AB. Calcola il rapporto tra le superfici e tra i volumi dei due solidi
che si ottengono facendo ruotare ABC di una rotazione completa prima attorno a r e poi attorno a s.
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Rsup ˆ
p
p 3
3
; Rvol ˆ
2
2
SUPERFICI E VOLUMI
Per la verifica delle competenze
1
ESERCIZIO GUIDA
Dimostra che il volume di un tronco di piramide regolare eÁ dato dalla formula V ˆ
Considera la piramide completa P di cui il tronco fa parte.
Sia h 0 la misura dell'altezza della piramide P 0 asportata per avere
il tronco; il volume del tronco si ottiene per differenza fra il volume della piramide completa P e quello della piramide P 0 :
V ˆ
1 …
B h ‡ h 0†
3
p
1
h b ‡ B ‡ bB .
3
1 0
bh
3
Ricorda poi che le due piramidi P e P 0 sono simili e che quindi le
basi B e b sono proporzionali ai quadrati delle altezze.
2
ESERCIZIO GUIDA
Dimostra che il volume di un tronco di cono circolare retto avente per basi i due cerchi di raggi R e r e
1
per altezza h eÁ dato da V ˆ h…R2 ‡ Rr ‡ r 2 †.
3
Indica con h 0 l'altezza del cono di vertice O che si ottiene dal completamento del tronco; procedendo
come nell'esercizio precedente, il volume del tronco eÁ dato da .............
V ˆ 1 R2 …h ‡ h 0 †
3
1 r 2 h 0 ˆ ::::::::::
3
Osserva ora la costruzione indicata in figura: i triangoli OAB e
BHD sono simili e percioÁ si puoÁ scrivere la proporzione
OA : BH ˆ AB : HD
Passando alle misure dei segmenti ricavi che h 0 ˆ :::::: e sostituendo nell'espressione del volume ottieni la formula cercata.
3
ESERCIZIO GUIDA
Dimostra che il volume di un segmento sferico a una base di altezza h di
1
una sfera di raggio r eÁ dato dalla formula V ˆ h2 …3r
3
h† .
Con riferimento alla figura a lato nella quale BH ˆ h e OC ˆ r, devi calcolare il volume del settore sferico avente vertice in O e da questo togliere il volume del cono di vertice O e avente per base il cerchio di raggio
HC.
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Applicando il secondo teorema di Euclide al triangolo ABC rettangolo in C trovi che: HC ˆ :::::::::::
L'area di base del cono eÁ quindi: ...............................
Il volume del cono, che ha altezza r
h eÁ: .................................
2
Ricordando che il volume del settore sferico eÁ uguale a r 2 h puoi trovare il volume richiesto.
3
4 Dimostra che il volume di un segmento sferico a due basi eÁ dato dalla formula ˆ 1 h r12 ‡ r22 ‡ 1 h3
2
6
dove h eÁ l'altezza del segmento, r1 e r2 sono i raggi delle due basi.
(Suggerimento: osserva che tale solido si ottiene per differenza dei volumi di segmenti sferici a una base
e segui un ragionamento simile a quello fatto per l'esercizio precedente)
5 Sezionando un cubo con un piano si possono ottenere alcuni poligoni regolari; individuali dando ampia
spiegazione delle tue considerazioni.
6 Dimostra che i volumi di una sfera, del cono equilatero circoscritto e quello del cilindro circoscritto sono, nell'ordine, proporzionali ai numeri 4,9 e 6.
Esame di Stato
(In corsivo le parti che possono essere svolte solo dopo aver completato lo studio dell'analisi nel quinto
anno di corso)
1 Un solido ha per base un cerchio di raggio 1. Ogni sezione del solido ottenuta con un piano perpendi
colare ad un prefissato diametro eÁ un triangolo equilatero. Si calcoli il volume del solido.
1 p
3
3
2 Un solido viene trasformato mediante una similitudine di rapporto 3. Come varia il suo volume? Come
‰V 0 ˆ 27V ; S 0 ˆ 9S Š
varia l'area della sua superficie?
3 Si provi che la superficie totale di un cilindro equilatero sta alla superficie della sfera ad esso circoscritta
come 3 sta a 4.
4 I centri delle facce di un cubo sono i vertici di un ottaedro. E' un ottaedro regolare? Quale eÁ il rapporto tra
‰6Š
i volumi dei due solidi?
5 Una piramide ha base quadrata e l'altezza uguale a 10cm. Quanti piani paralleli alla base dividono la
piramide in due parti i cui volumi sono nel rapporto 7 : 3? Quali sono le distanze di tali piani dal vertice
della piramide?
6 Un gioiello eÁ stato realizzato prevalentemente
in oro (peso specifico ˆ 19,32) e la sua forma geometrica
p
eÁ un tetraedro regolare di altezza 3cm. L'oro impiegato nella realizzazione del gioiello occupa il 75%
del volume del tetraedro. Qual eÁ stato il costo dell'oro se la sua quotazione al momento della realizza‰E 136,12Š
zione era di 8,35 euro per grammo?
7 Una piramide eÁ divisa da un piano parallelo alla base in due parti: una piramide e un tronco di piramide.
Il piano sezione divide l'altezza della piramide in due parti, di cui quella che contiene il vertice della
piramide eÁ doppia dell'altra. Stabilire se i dati sono o no sufficienti per calcolare il rapporto fra il volume
V ˆ
4p
della piramide recisa e quello del tronco di piramide.
V0
5‡
6
8 La capacitaÁ di un serbatoio eÁ pari a quella del cubo inscritto in una sfera di un metro di diametro. Quanto
‰192,45 `Š
sono, approssimativamente, i litri di liquido che puoÁ contenere?
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
9 Nei "Discorsi e dimostrazioni matematiche intorno a due nuove scienze", Galileo Galilei descrive la costruzione di un solido che si chiama
scodella considerando una semisfera di raggio r e il cilindro ad essa circoscritto. La scodella si ottiene togliendo la semisfera dal cilindro. Si
dimostri, utilizzando il principio di Cavalieri, che la scodella ha volume pari al cono di vertice V in figura.
10 Si sechi una sfera con un piano, in modo che il circolo massimo sia medio proporzionale tra le superfici
p
p appianate delle calotte nelle quali rimane divisa la sfera. altezza delle due calotte:
2‡ 3
2
3
r,
r
2
2
11 Un tetraedro e un ottaedro regolari hanno gli spigoli della stessa lunghezza `. Si dimostri che il volume
dell'ottaedro eÁ il quadruplo di quello dell'ottaedro.
12 Si consideri il cubo di spigoli AA 0 , BB 0 , CC 0 , DD 0 , in cui le facce opposte sono i quadrati ABCD e
A 0 B 0 C 0 D 0 . Sia E il punto medio dello spigolo AB. I piani ACC 0 A 0 e D 0 DE dividono il cubo in quattro
parti. Dimostrare che la parte piuÁ estesa eÁ il quintuplo di quella meno estesa.
13
ESERCIZIO GUIDA
Una piramide ha per base il triangolo ABC, isoscele e rettangolo in A, ed ha per altezza il segmento
p
AV. Inoltre la faccia VBC forma un angolo di 45 con il piano della base e lo spigolo VB eÁ lungo 2h 3,
dove h eÁ una lunghezza nota. Calcolare la distanza del vertice A dal piano della faccia VBC e trovare
p
per quale valore di h tale distanza vale 4 2.
Verificato che questo valore di h eÁ 4, con riferimento ad esso, secare la piramide con un piano parallelo alla base ABC e, proiettato ortogonalmente il triangolo sezione sulla base stessa, esprimere il volume del prisma triangolare cosõÁ ottenuto in funzione della sua altezza x.
Studiare, in rapporto alla questione geometrica, la funzione f …x† ricavata
e tracciarne l'andamento in un piano riferito ad un sistema di assi cartesiani
ortogonali Oxy.
Calcolare infine quanti, fra i punti della regione piana compresa fra il grafico di f …x† e l'asse x, escluso il contorno, hanno entrambe le coordinate
intere.
I parte.
Dopo aver costruito la figura come dettato dal problema, tracciamo l'altezza AH relativa all'ipotenusa del triangolo di base. Osserviamo che VA eÁ
perpendicolare al piano di ABC per ipotesi, AH?BC, allora, per il teorema
delle tre perpendicolari, il piano AVH eÁ perpendicolare a BC. Questo signid ˆ 45 .
fica che VHA
Il triangolo AVH quindi eÁ rettangolo e isoscele e la sua altezza AK rapprep
senta la distanza di A dal piano di VBC. Trovi che AK ˆ h 2.
a.
II parte.
Indicata con x l'altezza del prisma (osserva la seconda figura) e posto h ˆ 4 come richiesto dal problema, per avere il suo volume devi calcolare la misura del cateto AC 0 in funzione di x. Trovi che
f …x † ˆ x 3 16x 2 ‡ 64x.
SUPERFICI E VOLUMI
b.
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Non essendo ancora in possesso di strumenti adeguati, non puoi costruire in modo esatto il grafico della funzione; tuttavia, mediante una
costruzione per punti oppure mediante un software tipo Derive, puoi
ottenere un grafico approssimato come quello in figura.
c.
14
ESERCIZIO GUIDA
Considerato il rettangolo ABCD, il cui lato AB eÁ lungo a, condurre per B la perpendicolare alla retta
AC e chiamare H ed E i punti in cui essa taglia le rette AC e AD nell'ordine. Condurre quindi per H la
perpendicolare al piano della figura e su di essa prendere un punto P tale che HP  6AE.
Esprimere il volume della piramide avente per vertice il punto P e
per base il quadrilatero HDEC in funzione della lunghezza x del
segmento BH. Studiare poi la funzione f …x† ottenuta quando
a ˆ 1 e disegnarne il grafico G in un piano cartesiano ortogonale
Oxy.
Calcolare infine l'area di ciascuna delle due regioni piane delimitate da G e dalla retta di equazione 4y 9 ˆ 0.
Il volume della piramide eÁ dato dalla relazione
1
S…HDEC† HP
3
devi quindi calcolare l'area del quadrilatero HDEC e, visto che
HP  6AE, la misura del segmento AE.
L'area del quadrilatero eÁ la somma delle aree dei triangoli DHC e
EDC.
Completa dunque il procedimento che segue:
AH ˆ :::::::::: (teorema di Pitagora applicato al triangolo AHB)
CH ˆ :::::::::: (secondo teorema di Euclide applicato al triangolo ABC)
4
S…DHC† ˆ :::::::::: (base HC e altezza DK)
CB ˆ :::::::::: (primo teorema di Euclide applicato al triangolo ABC)
Osserva ora che i triangoli ABE e AHB sono simili, quindi
AE ˆ ::::::::::
ED ˆ ::::::::::
Hai ora tutto quello che serve per continuare da solo. Se hai svolto correttamente l'esercizio troverai
2
2
.
che f …x† ˆ 1 x
x
15 Sono dati una semicirconferenza
ipotenusa AC incontra
Q ISTITUTO ITALIANO EDIZIONI ATLAS
di diametro AB ˆ 4 ed il triangolo rettangolo ABC tale che la sua
r
2
. Si conduca una retta perpendicolare
in P e tale che la sua misura sia 8
5
SUPERFICI E VOLUMI
ad AB che incontra rispettivamente AB, ed AC in D, E ed F e siano E 0 ed F 0 le proiezioni di E ed F su
BC. Si studi, al variare di AD, la variazione del volume del solido S generato, in un giro completo attorno
ad AB, dal rettangolo EE 0 F 0 F.
Osservato che V ha due massimi relativi, si calcoli, quando V assume il suo valore massimo assoluto,
p 3 p 12
l'area della superficie totale di S.
4
2
V …x † ˆ
5
…4
x †j5x
2x j; S ˆ 2 3 3 ‡
5
15 ‡
5
16 Considerato il triangolo equilatero ABC, chiamare:
0
00
l C , C
i punti che dividono il lato AB in tre parti congruenti …AC 0 < AC 00 †;
0
00
l A , A
i punti che dividono il lato BC in tre parti congruenti …BA 0 < BA 00 †;
0
00
l B , B
i punti che dividono il lato AC in tre parti congruenti …CB 0 < CB 00 †.
Indicare quindi con:
0
00
l L il punto di intersezione dei segmenti AA e BB ;
0
00
l M il punto di intersezione dei segmenti AA e CC ;
0
00
l N il punto di intersezione dei segmenti BB e CC ;
0
00
l P il punto di intersezione dei segmenti BB e AA ;
0
l Q il punto di intersezione dei segmenti CC
e AA 00 ;
0
l R il punto di intersezione dei segmenti CC
e BB 00 .
1
di quella del triangolo ABC.
a. Dimostrare che l'area dell'esagono LMNPQR eÁ
10
9 2 p
b. Ammesso che l'area di tale esagono sia
h 3, dove h eÁ una lunghezza assegnata, calcolare il vo10
lume del solido generato dall'esagono quando ruota di mezzo giro attorno alla retta NR.
Z b
‰ f …x†Š2 dx che fornisce il volume di un solido di rotazione, dic. Supponendo nota la formula V ˆ a
mostrare le formule dei volumi di un cono e di un tronco di cono circolare retti. b: V ˆ
p
27 3 3
h
100
17 Su un piano eÁ assegnata la circonferenza di centro O e diametro AB ˆ 2 e sulla perpendicolare per
O al piano eÁ fissato un punto C tale che OC  AB. Sia il cilindro circolare retto che ha per base la
circonferenza e altezza OC. Si conduca un piano parallelo ad che incontra il segmento OC in un
punto O 0 e si consideri il solido formato dal cilindro circolare retto 0 , di base la circonferenza e altezza OO 0 , sormontato dalla sfera di diametro O 0 C. Si studi come varia il volume di detto solido al variare del raggio della sfera.
Nel caso in cui il volume diventa minimo si conduca un piano parallelo ad OC e tangente alla sfera che
sega il cilindro 0 secondo un rettangolo. Si calcoli il perimetro della proiezione di detto rettangolo dal
#
p
punto C sul piano . "
p
V ˆ
4 x3
3
2x ‡ 2 con x ˆ raggio della sfera; Vmin per x ˆ
2
; perimetro ˆ 3 2
2
18 Nel cubo di vertici A, B, C, D, E, F, G, H le facce ABCD ed EFGH sono opposte ed i segmenti AE, BF, CG
sono spigoli. Inoltre gli spigoli del cubo hanno lunghezza unitaria. Sullo spigolo BF prendere un punto P
tale che BP ˆ x.
a. Verificare che la distanza y di P dalla diagonale AG eÁ espressa dalla seguente funzione
r
2… 2
x
x ‡ 1†
yˆ
3
b. Di essa disegnare il grafico in un sistema di assi cartesiani ortogonali Oxy dopo aver trovato, fra l'altro, i suoi asintoti.
c. Considerato infine il volume del solido generato, in una rotazione completa attorno all'asse x, della
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
regione piana delimitata da tale grafico, dagli assi di riferimento e dalla retta di equazione x ˆ h (con
16
.
h > 0), calcolare per quale valore di h questo volume eÁ
‰c: h ˆ 2Š
9
19
ESERCIZIO GUIDA
Nel parallelepipedo rettangolo di vertici A, B, C, D, E, F, G, H le facce ABCD ed EFGH sono opposte
ed i segmenti AE, BF, CG sono spigoli. Inoltre:
AB ˆ 3x
AD ˆ 4x
AE ˆ 2a
x
essendo a una lunghezza nota e x una lunghezza incognita. Chiamato P il piede della perpendicolare
condotta da A alla retta FH, considerare il poliedro avente per vertici i punti A, B, F, E, P. Calcolare
a. il volume di b. il valore di x che rende massimo il volume di , il valore di a per il quale questo volume massimo eÁ
128
cm 3 e infine, per tale valore di a, l'area della superficie del solido di volume masuguale a
75
simo.
Il poliedro di cui si deve calcolare il volume eÁ una piramide avente
per base il rettangolo AEFB e vertice P; il piede K dell'altezza PK di
questa piramide cade sul segmento EF perche .......................
d eÁ retto perche ..................
L'angolo EPF
Allora i triangoli HEF e KEP sono simili perche .....................
Puoi ora trovare l'altezza PK ed il volume richiesto.
2
3
36 x; V ˆ 36 …2 ax 2 x 3 †;
PK
ˆ
6
7
25
25
6
7
p 2 5
4
4
1
628 ‡ 4 5809 cm
volume massimo per x ˆ a; a ˆ 1; S ˆ
3
75
20 EÁ dato in un piano il triangolo ABC rettangolo in B, con i lati AB ˆ a ed AC ˆ 2a. Si conducano, in
uno dei semispazi individuati da , i segmenti AA 0 , BB 0 e CC 0 perpendicolari ad e tali che
AA 0 ˆ BB 0 ˆ 4a e l'angolo BB 0 C 0 ˆ . Il candidato:
4
a. indicato con P un punto del segmento BB 0 e posto BP ˆ x, studi come varia la somma s ˆ AP ‡ PC 0
al variare di P, determinando in particolare, con metodo analitico o sintetico, il minimo ed il massimo
valore assoluto di s, e tracci in un piano riferito ad un sistema di assi cartesiani ortogonali Oxs la curva
2
3
p q
p p di equazione s ˆ s…x†;
6 s…x† ˆ a2 ‡ x 2 ‡ a2 22 8 3
6
q
4
p
p
smin ˆ a 23 6 3 per x ˆ a 5 3
2
2ax 4
3 ‡ x2;
7
7
5
p p
7 ; smax ˆ a 17 ‡ 6 per x ˆ 4a
b. dimostri che la faccia A 0 B 0 C 0 del solido T di vertici ABCA 0 B 0 C 0 eÁ un triangolo rettangolo;
c. calcoli la superficie totale ed il volume di T.
p
V ˆ 1 a3 4 3
2
p
p
6 ‡ 7 3 ‡ 21 2
1 ;Sˆ
a
2
21 Considerato il rettangolo ABCD, il cui lato AD eÁ lungo 8a, dove a eÁ una lunghezza nota, sia M il punto
medio del lato AB. Sulla perpendicolare al piano del rettangolo condotta per M prendere un punto V in
3
modo che il piano del triangolo VCD formi col piano del rettangolo un angolo tale che tan ˆ .
4
Mostrare che la superficie laterale della piramide di vertice V e base ABCD eÁ costituita da due triangoli
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
rettangoli e da due triangoli isosceli. Sapendo che l'area di tale superficie laterale eÁ 92a2 , calcolare la
lunghezza di AB. Constatato che tale lunghezza eÁ 5a, condurre un piano parallelo alla base della piramide e proiettare ortogonalmente su tale base il poligono sezione di con la piramide stessa, ottenendo in questo modo un prisma retto.
V ˆ 10 …6ax 2
9
a. Calcolare il volume del prisma
x3†
b. Determinare la posizione di per la quale il volume risulta massimo.
[volume massimo quando dista 4a dal vertice della piramideŠ
c. A completamento del problema, dimostrare che se i numeri reali positivi x, y variano in modo che la
loro somma si mantenga costante, allora il prodotto x 2 y eÁ massimo quando x ˆ 2y.
22 Si consideri in un piano un rettangolo ABCD i cui lati BC ed AB misurano rispettivamente a e 2a. Sia
AEF, con E 2 AB e F 2 CD, un triangolo isoscele la cui base AE ha misura 2r. Il candidato:
a. dimostri che una retta s parallela ad AB, a distanza x da essa, interseca i triangoli AEF ed AEC secondo
segmenti congruenti;
b. detta C1 la circonferenza di diametro AE ed appartenente al piano passante per AB e perpendicolare
ad , e detti T1 e T2 i coni di base C1 e vertici rispettivamente nei punti F e C, dimostri che le sezioni
C 01 e C 02 di detti coni con il piano 0 passante per la retta s e parallelo al piano , sono circonferenze;
c. determini i volumi dei coni T1 e T2 ;
d. determini, per via sintetica o analitica, il valore di x per il quale C 01 e C 02 sono tangenti esternamente.
T1 e T2 sono equivalenti e hanno volume ar 2 ; x ˆ 2ar
3
2a ‡ r
23 Considerare i coni circolari retti in cui eÁ uguale ad una lunghezza assegnata 2` la somma del doppio
dell'altezza con il diametro della base. Determinare l'espressione del volume di tali coni.
Calcolare poi il cono di volume massimo e stabilire se ha anche la massima area laterale. Nel cono di
volume massimo inscrivere poi il cilindro circolare retto avente la base sul piano di base del cono e vo3
lume massimo. 2
1
1
… 2 r 3 †; indicato con x il raggio di base del cono, volume massimo per x ˆ `;
6 V ˆ 3 `r
3 7
4
5
non ha area laterale massima; altezza del cilindro di volume massimo 1 `
18
24 Sia S una semisfera di centro O e raggio 1 e
perpendicolare al piano di
la sua circonferenza massima. Sulla semiretta di origine O,
p
e che interseca S in A, si consideri il punto B tale che OB ˆ 3. Il candidato:
a. individui il punto C del segmento OA, centro dell'ulteriore cerchio d'intersezione di S con il cono di base e di vertice B;
b. detto P un punto del segmento OA la cui distanza da O sia x, scriva in funzione di x i volumi dei coni
di vertice O e di base rispettivamente i cerchi 1 e 2 , ottenuti dall'intersezione del piano per P perpendicolare ad OA con S e con ;
c. considerata la corona circolare W delimitata da 1 e 2 , determini il volume V …x † del solido delimitato da W e dalle superfici laterali dei coni anzidetti;
d. disegni, in un piano riferito ad un sistema di assi cartesiani ortogonali Oxy, la curva di equazione
"
#
p
2
V ˆ V …x†.
p
p
a: OC ˆ
3
; b. V1 ˆ x
2
3
3p x
3
, V 2 ˆ x …1
3
x 2 †; c. V …x † ˆ 2 3x 2
9
2x 3 25 In un piano eÁ assegnato il triangolo ABC, retto in B, i cui cateti AB e BC misurano rispettivamente 4 e 3.
Si conduca per il punto A la perpendicolare al piano e sia V un punto di questa per cui VA ˆ AB.
Il candidato:
a. dimostri geometricamente o algebricamente che, come tutte le altre facce del tetraedro VABC, anche
d
la faccia VBC eÁ un triangolo rettangolo il cui angolo retto eÁ VBC;
b. calcoli il volume e la superficie totale del tetraedro;
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
c. detto 2 il punto medio di VA e P un punto dello stesso segmento a distanza x da V, esprima in funzione di x il volume v del tetraedro MPQR, essendo Q ed R le rispettive intersezioni degli spigoli VB e
VC con il piano parallelo ad e passante per P;
d. studi come varia v al variare di P sul segmento VA, determinando in particolare la posizione P di P in
cui il volume v assume valore massimo assoluto;
e. detto D il punto medio di VB ed E il punto di AC tale che AE ˆ AB, determini la posizione P di P
che rende minima la somma DP ‡ PE.
(Suggerimento: si consiglia di far ruotare il triangolo VAB attorno ad AV fino a portarlo nel piano del
triangolo VAE, simmetricamente a quest'ultimo, e considerare la somma D 0 P ‡ PE, essendo D 0 il corrispondente di D nella suddetta rotazione)
p
b: VVABC ˆ 8, St ˆ 24 ‡ 6 2; c. v …x † ˆ 1 x 2 jx
8
2j; d. massimo assoluto per x ˆ 4; e. P V ˆ 8
3
p
26 Il triangolo ABC, rettangolo e non isoscele, eÁ la base di una piramide di altezza 3a 3 2. Le misure dei suoi
cateti sono date da due delle tre radici dell'equazione 4x 3 11ax 2 ‡ 10a2 x 3a3 ˆ 0. Il candidato:
a. determini la distanza k di un piano dal vertice della piramide sapendo che eÁ parallelo al piano del
triangolo ABC e taglia la piramide in due parti equivalenti;
b. determini k nel caso in cui il triangolo ABC ha un cateto che misura a e l'altro cateto eÁuna soluzione,
approssimata con due cifre significative, dell'equazione x 3 ‡ 4a2 x 2a3 ˆ 0;
c. esponga il procedimento utilizzato per il calcolo approssimato della radice dell'equazione proposta.
‰a: 3a; b: 3aŠ
27 La misura, in decimetri, del raggio di una sfera eÁ data dalla soluzione dell'equazione di terzo grado
2
3
…x 1† ‡x 2 ˆ x …x 1† ‡4. Nella sfera sono inscritti due coni circolari retti aventi la base comune e
3
le superfici laterali nel rapporto . Il candidato calcoli:
4
a. il rapporto fra i volumi dei due coni
b. la misura del raggio della base comune dei coni
c. il peso, approssimato ai grammi, del solido costituito dai due coni, supposto che sia realizzato con
legno di noce di peso specifico 0,82.
9
12
a.
16
; b.
5
28 Assegnato il segmento AB di lunghezza 1, si disegni la circonferenza avente il centro C sull'asse di AB e
passante per A e per B. In tale contesto, denotata con P la proiezione ortogonale di B sulla retta AC:
2
2
d ˆ x;
a. si esprima BC ‡ BP in funzione dell'angolo BAC
2
2
b. si stabilisca per quale valore di x si ha BC ‡ BP ˆ 7 ;
4
c. fissato x ˆ 30 , si calcoli il volume del solido che si ottiene dalla rotazione completa del triangolo
p BCP attorno alla retta AC, presa come asse di rotazione.
1
; c. 3 2
x;
b.
‡
sin
a.
2
4 cos x
6
72
Risultati di alcuni esercizi.
3 b.
10 d.
12 b.
13 c.
46 a. V, b. V, c. F, d. F, e. V, f. F
49 c.
50 b.
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
Testfinale di autovalutazione
C ONOSCENZE
1 E' dato un parallelepipedo rettangolo a base quadrata di lato ` e di altezza h; un piano parallelo alle basi lo
divide in due parallelepipedi di volume uno doppio rispetto all'altro; si puoÁ dire che:
a. l'area del poligono sezione misura:
¬
`2
­
1 `2
2
®
2`2
b. il rapporto fra le altezze dei due parallelepipedi eÁ:
c. il rapporto fra le due superfici laterali eÁ:
¬
¬
4
4
­
­
3
3
®
®
2
2
15 punti
2 Un cono e un cilindro hanno lo stesso volume e la stessa altezza; il rapporto fra i loro raggi di base eÁ:
p
p
a. 2
b. 2
c. 3
d. 3
15 punti
3 Le aree A e A 0 delle superfici di due tetraedri regolari sono tali che A0 ˆ 4; il rapporto fra i loro volumi:
A
a. non si puoÁ calcolare
b. eÁ 16
c. eÁ 4
d. eÁ 8
20 punti
4 I centri delle facce di un cubo sono i vertici di un ottaedro regolare. Se lo spigolo del cubo eÁ `, la superficie di
tale solido eÁ:
p
p
3
2
2
a. 3`
b. `
d. 6`2
c. 3 `2
20 punti
2
2
5 Indicato con l'angolo che una diagonale di un cubo forma con una faccia, si ha che:
p
p
p
3
3
b. ˆ arccos
c. ˆ arctan 6
a. ˆ arcsin
3
6
3
Esercizio
1
2
3
4
5
p
d. ˆ arctan 2
20 punti
Totale
Punteggio
Voto: totale ‡ 1 ˆ
10
42
SUPERFICI E VOLUMI
Q ISTITUTO ITALIANO EDIZIONI ATLAS
A BILITÀ
1 In una piramide regolare a base quadrata, l'area della superficie laterale eÁ 60a2 e l'altezza eÁ lunga 4a. Calcola la misura del volume del solido.
15 punti
2 Un cono circolare retto ha come sviluppo laterale un settore circolare di raggio r e di ampiezza 60 ; qual eÁ il
suo volume?
15 punti
3 Una piscina ha la superficie libera a forma di rettangolo con i lati che
misurano 15m e 8m. Il profilo della sua sezione verticale eÁ visibile in
figura. Quanti litri di acqua puoÁ contenere? Per pulirla si usa un robot
che non riesce a superare i 28 di inclinazione; eÁ possibile pulire completamente il fondo della piscina?
15 punti
4 Il rapporto fra la base maggiore e la base minore di un trapezio isoscele eÁ 4. Stabilire se si puoÁ determinare il
rapporto fra i volumi dei solidi ottenuti facendo ruotare il trapezio di un giro completo dapprima attorno alla
base maggiore e poi intorno alla base minore o se i dati a disposizione non sono sufficienti.
(dal questionario dell'esame di Stato 2002)
20 punti
5 Un prisma retto eÁ inscritto in una piramide triangolare regolare; la base del prisma eÁ la sezione della piramide
con il piano equidistante dal suo vertice e dalla sua base. Se il volume della piramide eÁ 120cm3 , qual eÁ il volume del prisma?
25 punti
Esercizio
1
2
3
4
5
Totale
Punteggio
Voto: totale ‡ 1 ˆ
10
Q ISTITUTO ITALIANO EDIZIONI ATLAS
SUPERFICI E VOLUMI
43
Soluzioni
C ONOSCENZE
1 a.
¬, b. ®, c. ®
2 c.
3 d.
4 a.
5 a.
A BILITÀ
p
1 Indicando con 2x la misura del lato di base, l'apotema misura x 2 ‡ 16a2 . Si puoÁ quindi scrivere l'equazione
p
4x x 2 ‡ 16a2 ˆ 60a2 che ha soluzione x ˆ 3a. Il volume della piramide eÁ quindi 48a3 .
2 La lunghezza dell'arco del settore circolare rappresenta la lunghezza della circonferenza di base del cono ed eÁ
r p
r
r
1
1
1 2
35
r.
; il raggio di base del cono eÁ quindi R ˆ
ˆ r; l'altezza del cono eÁ h ˆ r 2
r ˆ
6
3
3 2
6
36
p
p
35 1
35 3
r2
r ˆ
r .
Il volume eÁ dunque V ˆ 6
648
36
3
3 Il volume della piscina eÁ di 352,5m3 ; la sua capacitaÁ in litri eÁ 352 500. L'inclinazione rispetto alla linea orizzontale dei lati obliqui del profilo eÁ di 26,6 circa, quindi il robot riesce a pulire il fondo.
4 Dalla rotazione attorno alla base maggiore: V ˆ 2h2 b. Dalla rotazione attorno alla base minore: V ˆ 3h2 b.
2
Rapporto:
3
I punti D, E, F sono i punti medi degli spigoli della piramide. L'area del trian-
5
4
4
1
golo DEF eÁ quindi dell'area di ABC. Posto area …ABC† ˆ S
4
V…piramide† ˆ
V…prisma† ˆ
Quindi
SUPERFICI E VOLUMI
si ha:
1
S VH
3
1
1
1
S VH ˆ S VH
4
2
8
V…prisma† ˆ
3
3
V
ˆ 120cm3 ˆ 45cm3
8 …piramide† 8
Q ISTITUTO ITALIANO EDIZIONI ATLAS