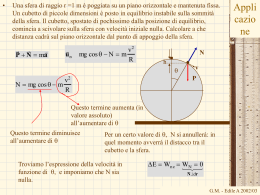
Appli
cazio
ne
Nel momento in cui il semaforo volge al verde , un’auto parte con
accelerazione costante a=2.2 m/s2. Nello stesso istante un autocarro che
sopravviene alla velocità costante di 9.5 m/s sorpassa l’auto.
a) A quale distanza oltre al semaforo l’auto risorpasserà il camion?
b) Quale sarà la velocità dell’auto in quel momento?
a) A quale distanza oltre al semaforo l’auto risorpasserà il camion?
Iniziamo a contare il tempo a partire dal momento in cui il semaforo diventa
verde (t=0s).
Introduciamo un asse di riferimento lungo la strada rettilinea. Fissiamo
l’origine nel punto in cui è ferma l’automobile in attesa del verde.
Orientiamo l’asse nel verso del moto del camion e dell’automobile.
Con queste scelte le condizioni iniziali sono:
Auto
xAo=0 m
vAox=0 m/s
aAox=2.2 m/s2
Camion
xCo=0 m
vCox=9.5 m/s
aCox=0 m/s2
A
C
O
x
Le rispettive leggi orarie
diventano:
x A (t)  12 a A xot 2
v Ax (t)  a Axo t
x C (t)  v Cx ot
v Cx (t)  v Cx o
G.M. - Edile A 2002/03
Ci sarà il risorpasso dell’auto quando le posizioni dell’auto e del camion
saranno nuovamente uguali.
x A (t)  xC (t) 
1
2
a Ax ot 2  vCx ot
Appli
cazio
ne
Calcoliamo l’istante di tempo quando questa situazione si verifica:
1
2
a Axo t 2  vCxo t 
1
2
a Axo t 2  vCxo t  0
2
1
a
t
2 Axo
 vCxo t  0
 t12 a A t  vC  0
xo
xo

2vC xo
t1  0 t 2 
a A xo
t1 corrisponde all’istante in cui il camion sorpassa l’auto ferma, anche in quel
caso infatti le posizioni dei due veicoli coincidevano.
L’istante del risorpasso sarà t2.
2  9.5 m s
t2 
La velocità dell’auto in
quell’istante sarà:
2.2 m
 8.64s
s2
v Ax (t)  aAxot  2.2 ms2  8.64s  19.01ms
G.M. - Edile A 2002/03
La posizione in cui avviene il risorpasso, la possiamo calcolare con una delle
due leggi orarie:
x A (t)  12 a A x ot 2x C (t)
xC (t)  12 2.2 m s2 8.64 2 s2  82.1m
x C (t)  v C x ot
x C (t)  9.5 m s 8.64s  82.1m
La velocità dell’auto in
quell’istante sarà:
v Ax (t)  aAxot  2.2 ms2  8.64s  19.01ms
Appli
cazio
ne
G.M. - Edile A 2002/03
Dall’ugello della doccia sgocciola l’acqua cadendo sul fondo posto 2.00 m
più in basso. Le gocce cadono ad intervalli regolari. La quarta goccia si
stacca nel momento in cui la prima arriva la suolo. Trovare le posizioni della
seconda e terza goccia in quell’istante.
Appli
cazio
ne
• Ogni quanto tempo cade una goccia?
– Nel tempo impiegato da una goccia a percorre i 2 metri di dislivello ne
sono cadute 3 (sono trascorsi 3 intervalli).
– E’ essenziale capire quanto tempo una goccia impiega a percorrere i 2
metri tra l’ugello e il fondo.
• Studiamo il moto di una goccia:
– il moto è uniformemente accelerato, accelerazione di gravità.
– Facciamo partire il cronometro nell’istante in cui la goccia si stacca
dall’ugello.
– Fissiamo un asse di riferimento verticale, orientato verso l’alto, con
l’origine sul fondo.
– Con questa scelte le condizioni iniziali sono:
• xo=2m
• vxo=0m/s
• axo=-g=-9.81m/s2 l’accelerazione di gravità è diretta verso il basso
G.M. - Edile A 2002/03
• La legge oraria della goccia sarà:
x(t)  x o  12 gt 2
v x (t)  gt
x(t f )  x o 
2
1
gt
2
f
L’istante tf in cui la goccia tocca il fondo si può
calcolare imponendo che la posizione in
quell’istante sia nulla:
2x o
 0  tf  

g
Appli
cazio
ne
2  2m
 .63s
m
9.81 s 2
La durata del moto della goccia è dato da
tf -ti
Poiché ti è uguale a zero la durata è tf =.63s
L’intervallo tra una goccia e la successiva è un
terzo di questo valore Dt=.21s
Per sapere dove si trovano le gocce due e tre nel momento in cui la
prima tocca il fondo, basterà calcolare dove si trovava la goccia 1 dopo
un Dt e dopo due Dt.
x(Dt)  xo  12 gDt 2  2m  12 9.81 .212 1.78m
x(2Dt)  x o  12 g2Dt 2  2m  12 9.81 .422  1.13m
G.M. - Edile A 2002/03
Per provare una palla da tennis la si lascia cadere da una altezza di 4.00 m
dal pavimento. Rimbalza fino ad un altezza di 2.00 m. Se è stata in contatto
con il suolo per 12.0 ms, qual è stata la sua accelerazione media durante il
contatto.
Appli
cazio
ne
• La palla da tennis arriva al suolo con una velocità diretta verso il
basso
• Poiché rimbalza verso l’alto, riparte dal suolo con una velocità diretta
verso l’alto.
• C’è stata quindi una variazione di velocità. C’è stata una
accelerazione!
• Fissiamo l’asse y di riferimento diretto l’alto, coincidente con la
verticale passante per il punto di impatto, con l’origine nel punto di
impatto.
a my 
vyf  vyi
Dt
Occorre calcolare la velocità finale e
quella iniziale sull’intervallo di tempo in
cui la palla è a contatto con il suolo.
La velocità iniziale è quella con cui arriva
al suolo dopo la caduta di 4 m
La velocità finale è quella con cui riparte
dal suolo.
G.M. - Edile A 2002/03
• Il moto di caduta è un moto uniformemente accelerato (accelerazione
di gravità)
• Nel sistema di riferimento scelto, supponendo di far partire il
cronometro nel momento del lancio, le condizioni iniziali valgono:
– yo= 4.00m
– voy=0m/s
– aoy=-g=-9.81m/s2
Appli
cazio
ne
y(t)  y o  12 gt 2
v y (t)  gt
• La legge oraria vale:
• L’istante in cui la palla raggiunge il suolo si ottiene imponendo che
y(tf)=0 (va preso l’istante positivo, il suolo viene raggiunto dopo che
la palla è partita)
y(t f )  y o  12 gt 2f  0  t f  
• La velocità in quell’istante sarà:
2yo

g
2  4m
 .903s
m
9.81 s 2
v y (t)  gt f  9.81 ms2 .903s  8.85 ms
• Il valore che abbiamo trovato è il valore della velocità iniziale da
utilizzare nella formula dell’accelerazione media.
G.M. - Edile A 2002/03
Appli
cazio
ne
• Per calcolare la velocità finale da usare nella formula
dell’accelerazione media dobbiamo studiare il moto di risalita.
• Anche il moto di risalita è un moto uniformemente accelerato
(accelerazione di gravità)
• Nel sistema di riferimento scelto, supponendo di far ripartire il
cronometro nel momento in cui la palla lascia il suolo, le condizioni
iniziali valgono:
– yo= 0.00m
– voy=? da determinare
– aoy=-g=-9.81m/s2
y(t)  v oyt  12 gt 2
v y (t)  voy  gt
• La legge oraria vale:
• Ricavando il tempo dalla seconda eq. e sostituendo nella prima: t  
vy  vo y 
v y  vo y 

1 


gt  vo y 
2g 




g
g 
2
y
v o yt   12
y
vo yvy
• Da cui:
g

v y  voy
g
2
v 2o y
g
 12 g
v 2y
g
2
 12 g
v2o y
2
g
g
v o yv y
2
g

1
2
v2o y
g
2
v
1 y
2
g
v 2y  v2oy  2gy
G.M. - Edile A 2002/03
Appli
cazio
ne
• Abbiamo ottenuto l’espressione della velocità in funzione dalla
posizione
v 2y  v2oy  2gy
• Il modulo della velocità a parità di posizione è lo stesso sia nel moto
di risalita che in quello di discesa.
• Quando la coordinata y è 2m, il punto più in alto della traiettoria, la
velocità è nulla:
2
 vo y  2gy max
• Possiamo ricavare voy:
v o y  2gy max  2  9.81m s 2  2m  39.24 m
2
s2
 6.26 m s
• Ciò che abbiamo trovato è la velocità finale relativa all’intervallo di
tempo in cui la palla è a contatto con il suolo.
• L’accelerazione media in questo intervallo di tempo vale dunque:
a my 
v yf  v yi
Dt
6.26 m s  8.85 m s 

 1256 ms 2
3
12  10 s
G.M. - Edile A 2002/03
Accelerazione in funzione della
posizione
• In alcuni casi l’accelerazione è nota in funzione della posizione del
punto materiale ax(x).
– Quindi non si conosce direttamente ax (t), ma la dipendenza dal
tempo è nota solo attraverso la legge oraria x(t), ax (x(t)).
dv x (t)
 a x (x)
dt
• L a definizione di accelerazione ci dice che in ogni intervallo
infinitesimo dt, il rapporto tra la variazione di velocità dvx e l’intervallo
di tempo dt è proprio uguale all’accelerazione.
• Indichiamo con dx lo spostamento infinitesimo subito dal punto
materiale nell’intervallo di tempo dt
– Se il corpo non è fermo, dx sarà in generale piccolo (infinitesimo)
ma diverso da zero.
– Possiamo allora moltiplicare entrambi i membri dell’equazione
precedente per dx
G.M. - Edile A 2002/03
Accelerazione in funzione della
posizione
• Otteniamo che in ogni intervallo infinitesimo dt vale la seguente
uguaglianza:
dv x
dx  a x (x)dx
dt
• Osservando che dx/dt è la velocità vx, si ottiene:
dx
dv x
 v xdv x  a x (x)dx
dt
v xdv x  ax (x)dx
• Sommando su tutti gli intervalli infinitesimi in cui abbiamo suddiviso
l’intervallo di osservazione del moto, otteniamo:
f
f
 v dv   a (x)dx
i
x
• Integriamo il primo membro:
f
 v dv
i
x
x
x
i
x
La variabile di integrazione è vx
La funzione integranda è f(vx)= vx
La primitiva F(vx)= v2x/2
G.M. - Edile A 2002/03
Accelerazione in funzione della
posizione
f
v2x  v 2xf v2xi
v xdv x    

2
2
i
 2 i

• Pertanto:
f
• In conclusione otteniamo:
v 2xf

v 2xi

f
 2 a x (x)dx
i
• Naturalmente per integrare il secondo membro doppiamo conoscere
l’espressione di ax(x).
• Esaminiamo il caso in cui l’accelerazione ax(x) è costante, ax(x)= axo.
v 2xf
 v 2xi

f

f
 2 a xodx  2a xo dx  2a xoxfi  2a xo (xf  x i )
i
i
• Chiamando, come al solito, vxi=vxo, xi=xo, xf=x(t) e vxf=vx(t)
v 2x (t)  v2xo  2a xo(x(t)  x o )
• Che ci da l’espressione di v in funzione di x
•
v 2x  v2xo  2axo (x  xo )
Da confrontare con quanto abbiamo già trovato nel moto di caduta dei gravi.
v 2y  v2oy  2gy
G.M. - Edile A 2002/03