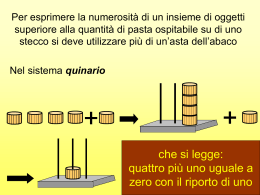
I laboratori del Giardino di Archimede dedicati alla storia della numerazione: un percorso dalla Scuola dell’Infanzia alla Scuola Superiore
Raffaella Petti
Il Giardino di Archimede – Un Museo per la Matematica, Firenze
Sunto
Riferendosi ai laboratori dedicati ai sistemi di numerazione svolti al Giardino di Archimede, se ne presentano alcuni aspetti e si propone qualche riflessione su come i vari temi possano essere oggetto di attività diverse dirette a fasce di età che vanno dalla scuola dell'Infanzia alla Scuola Superiore.
I laboratori al Museo
La parte museale della sede di Firenze del Giardino di Archimede è oggi composta da diverse sezioni che si sono aggiunte al primo nucleo costituito dalla mostra Oltre il Compasso. Un elenco completo con descrizione e materiali si può trovare sul sito del museo: www.archimede.ms.
Per le scuole sono predisposti diversi percorsi di visite guidate attraverso le sezioni della mostra.
Oltre alle visite guidate vengono effettuati al museo laboratori su temi diversi. Anche per questi si rimanda al sito web.
In questo intervento ci occuperemo di un gruppo di laboratori che prendono spunto da diversi momenti della storia della numerazione:
­ Numeri e conti presso gli antichi sumeri (Infanzia, Primaria, Secondaria Inferiore e Superiore)
­ I geroglifici degli antichi egizi (Infanzia, Primaria, Secondaria Inferiore e Superiore)
­ Le tavole di conto (Primaria, Secondaria Inferiore e Superiore)
­ Pallottolieri giapponesi (Primaria, Secondaria Inferiore)
­ Bastoncini cinesi per numeri e conti (Infanzia, Primaria, Secondaria Inferiore)
­ Tecniche varie di moltiplicazione (Primaria secondo ciclo, Secondaria Inferiore e Superiore)
­ Bastoncini per moltiplicare e dividere (Primaria secondo ciclo, Secondaria Inferiore e Superiore)
Ciascuno di questi temi prevede attività differenziate a seconda delle età che possono andare dai 4­5 anni della scuola dell'infanzia fino alle Scuole Superiori. Come premessa vorremmo richiamare l'attenzione sull'aspetto storico che accomuna questi laboratori. Gli esempi che toccheremo intendono infatti fornire degli spunti di riflessione sul ruolo che la storia della matematica può avere nelle attività di comunicazione del museo ed anche nella didattica della matematica. Fra le motivazioni di carattere generale nell'uso della storia vi è quella di poter collocare la matematica in una più ampia prospettiva culturale e sanare la frattura fra discipline umanistiche e scientifiche: il percorso storico evidenzia una matematica in continuo divenire, frutto di contributi diversi, e non scienza preconfezionata e statica.
Ma vi è una motivazione più specifica, con aspetti direttamente spendibili proprio a livello laboratoriale, che ci interessa in questo contesto. Calandosi in un determinato momento storico la storia infatti può fornire contesti e strumenti facilmente acquisibili e direttamente utilizzabili per fare matematica. Non sempre la storia di un'idea matematica è fatta di passi intermedi più semplici del prodotto finale, ma nel caso della storia della numerazione in molti casi accade proprio così. Qui lo sviluppo storico delle idee e lo sviluppo cognitivo di ciascun individuo presentano molte analogie. Il sistema di numerazione che noi utilizziamo è, per così dire, un sistema adulto, sicuramente molto efficace, ma che nasconde diverse difficoltà. Si tratta di difficoltà di tipo epistemologico, difficoltà tecniche, difficoltà riconducibili all'astrazione del linguaggio e all'aspetto formale. Alcune di queste possono venire affrontate gradualmente o indagate in aspetti meno evidenti ricorrendo appunto ad altri sistemi di numerazione.
Un altro aspetto didatticamente significativo da citare riguarda il coinvolgimento nelle varie attività. Nel momento in cui si mette in mano ai bambini uno strumento nuovo ma che si collochi in un momento precedente, che sia strumento concreto o conoscenza da utilizzare, si offre la possibilità di partire da un passo indietro, pareggiando il livello di partenza e recuperando la partecipazione di tutti. In questo intervento daremo per noto il funzionamento dei sistemi di numerazione citati di cui forniremo solo qualche richiamo, dove necessario. Eventuali informazioni si possono trovare su vari testi di storia della matematica. Tra i più completi ricordiamo ad esempio Ifrah, Storia universale dei numeri. Vorremo invece guardare ai laboratori del Giardino di Archimede offrendo non tanto una presentazione sommaria delle attività di ciascuno dei diversi laboratori, quanto un'idea delle diverse sfaccettature che si possono cogliere nelle varie attività, anche quando riferite agli stessi argomenti fondanti. Per fare ciò abbiamo scelto semplici esempi, come la rappresentazione di una quantità, la tecnica di calcolo, le operazioni inverse, che ritrovandosi in diversi laboratori permettono di attraversali trasversalmente.
La rappresentazione di una quantità
La rappresentazione delle quantità sta in qualche modo proprio alle origini della matematica sia nel senso storico che in quello dello sviluppo cognitivo. In questo secondo senso ci offre modo di gettare un'occhiata al lavoro che si può fare con i piccoli nei laboratori.
Rappresentare la quantità di un gruppo di oggetti significa esprimere quella caratteristica che non dipende dalle specificità degli oggetti ma solo dal loro numero. Una caratteristica che per alcuni limitati (poco numerosi) insiemi si percepisce immediatamente, in altri casi si ottiene tramite un'operazione di conteggio. L'operazione di conteggio usuale presenta molti aspetti delicati. Si appoggia a uno “strumento”, che è il cosiddetto “registro di conteggio”, cioè la successione dei nomi dei numeri “uno, due, tre, ...”. Fra le difficoltà del suo utilizzo segnaliamo che è formato da elementi astratti, non ha limite, gli elementi sono rigidamente ordinati. Inoltre il risultato che si ottiene attraverso il conteggio è un'etichetta verbale (o un simbolo numerico) che non tiene conto del percorso compiuto per raggiungerlo. Insomma, il nostro modo di contare è piuttosto tortuoso e si serve di abilità già piuttosto avanzate.
Volendo semplificare, per rappresentare una quantità basterebbe spogliare un insieme di oggetti delle loro caratteristiche specifiche per lasciare solo quelle che riguardano la numerosità. Si potrebbe allora contare in un modo più semplice?
Vediamo cosa ci offrono gli antichi sumeri che, all'origine della storia, con lo sviluppo di società sempre più complesse, si trovano nella necessità di registrare e operare con le quantità delle merci prodotte e scambiate. Ancora prima della nascita della civiltà sumera, nell'area mesopotamica si hanno delle prime attestazioni in questo senso: gli scavi hanno portato alla luce piccoli oggetti in terracotta che rappresentano i diversi prodotti. Così ad esempio un disco con una croce rappresenta una pecora, tre dischi tre pecore, dodici dischi dodici pecore. Per rappresentare capre, misure di orzo, giare di olio, ..., si ricorreva a oggetti diversi. Questo può rappresentare un primo passo verso l'astrazione: l'oggetto vero si sostituisce con un oggetto simbolico, ma non è ancora una vera e propria rappresentazione della quantità perché l'oggetto che “conta” le pecore è diverso da quello che conta le capre o le giare di olio. Presto si compie però un passo decisivo: in una fase successiva si passa a utilizzare sassolini generici, tutti uguali e appositamente costruiti allo scopo. Questi oggetti sono noti come “calculi”, sassolini. Nei laboratori ispirati al sistema di numerazione degli antichi sumeri al livello più elementare, a partire dai quattro anni della Scuola dell'Infanzia, si lavora usando i coni di argilla. Nel sistema sumero il cono rappresenta l'unità. Dove è possibile (cioè quando il laboratorio è articolato in più incontri) ogni bambino costruisce i suoi conetti, che diventano sostituti delle dita delle mani: si costruiscono “le dita” prima di una e poi dell'altra mano, per un totale di dieci coni. Quando nei laboratori si conta con i conetti, non si richiede che si sappia “contare” inteso come il nostro contare da adulti: con i conetti si può contare nel senso che ogni oggetto dell'insieme da contare viene sostituito da uno dei “calculi”, uno ad uno, senza richiedere la “filastrocca dei numeri”, uno, due, tre ..., che verrà eventualmente in seguito.
In un secondo momento, quando le varie situazioni lo richiedano, si può aumentare il numero dei coni, staccandosi dalla stretta corrispondenza con le dita.
Quando poi si inizia ad avere a che fare con quantità sempre più grandi ci si scontra con nuove difficoltà: un mucchio troppo numeroso di sassolini perde la sua efficacia nella rappresentazione della quantità. Come si può aver ragione di un grande numero di sassolini tutti uguali tra loro? Si apre la necessità di organizzarli, riconducendoli a quantità familiari, ad esempio raccogliendo tanti gruppetti tutti uguali tra loro. In altre parole si sta creando una base per la numerazione.
Nella numerazione sumera il primo livello di raggruppamento è costituito da dieci conetti. Questi vengono sostituiti da un unico nuovo sassolino: il sassolino sferico che rappresenta la decina. Si tratta un altro piccolo passo verso l'astrazione, piccolo ma importante e significativo perché ora un oggetto simbolico ne sostituisce altri. Nel conteggio non si ha più una corrispondenza uno a uno con gli oggetti da contare. Nel sassolino sferico si deve poter cogliere il duplice aspetto di uno e dieci.
Nelle varie attività con i piccoli per questi passi e alcuni dei successivi ci si appoggia a una cornice narrativa fornita da un racconto che narra le vicende di un bambino (Uri, il piccolo sumero, S. Frasca ­ R. Petti) e che ripercorre in forma romanzata le tappe fondamentali della storia della numerazione sumera.
Gettando uno sguardo oltre, la strada ormai è aperta per affrontare quantità sempre maggiori. Nella numerazione sumera i raggruppamenti non procedono di dieci in dieci, come nella nostra, ma alternano il dieci con il sei, così i sassolini che hanno le forme di cono, sfera, grande cono, grande cono con il buco, grande sfera, grande sfera con il buco, rappresentano i valori uno, dieci, sessanta, seicento, tremilaseicento, trentaseimila. Ma per poterli usare basterà saper riconoscere gruppi di dieci o di sei. figura1
Parallelamente si percorre il tema del passaggio da una rappresentazione per mezzo di oggetti simbolici a una rappresentazione scritta con simboli astratti. Seguendo quello che è stato l'effettivo sviluppo storico, si propongono graduali passi successivi in questa direzione. Così dalle impronte lasciate dai singoli “calculi” su panetti di argilla si passa alla riproduzione di tali impronte con bastoncini a sezione rotonda, si arriva alla scrittura cuneiforme sumera in cui i simboli numerici sono il disegno delle originarie forme dei sassolini fatte a mezzo di cunei, per arrivare infine alla semplificazione dei segni che si riducono a due nella cuneiforme posizionale babilonese. Questa si è ormai ben allontanata dagli originari “calculi” dei quali ripropongono l'alternanza dei gruppi di dieci e di sei che li caratterizza per estendere questa struttura a piacere, anche oltre le prime potenze del sessanta da una parte e, dall'altra, alle frazioni.
figura2
La scrittura posizionale babilonese permette di toccare con i più grandi (Scuole Secondarie) vari aspetti di matematica più avanzata. Ad esempio si possono esplorare i caratteri della posizionalità, confrontando il nostro sistema con quello babilonese e scoprendo i motivi dei limiti e delle ambiguità che questo ultimo presenta. L'estensione della rappresentazione posizionale alle frazioni dell'unità (praticata nei testi babilonesi) porta a riflessioni sulla conseguenza della diversa base (decimale o sessagesimale) sulla limitatezza delle rappresentazioni dei numeri frazionari in notazione posizionale, e dunque sulla caratterizzazione dei razionali.
Alcune delle considerazioni che abbiamo presentato a proposito della numerazione sumera possono ripetersi per gli altri sistemi di numerazione oggetto di laboratori. D'altra parte le caratteristiche specifiche di ciascuno degli altri sistemi permettono di mettere in evidenza altri aspetti. Consideriamo ad esempio quello degli antichi egizi. Questi si servivano di diversi segni geroglifici, corrispondenti ai nostri valori 1, 10, 100, 1000, 10000, 100000, 1000000. Tali segni possono essere ripetuti un certo numero di volte e il valore numerico di una scrittura è dato dalla somma dei singoli valori che vi compaiono. Nella forma in cui la conosciamo la rappresentazione egizia è una forma scritta (scritta su papiri o dipinta o scolpita su pietra), ma il geroglifico di valore unitario, il bastoncino, ci suggerisce che probabilmente anche questa rappresentazione nasce da una pratica di registrazione per mezzo di oggetti concreti: qui bastoncini, come per i sumeri i sassolini. La base strettamente decimale offre lo spunto per lavorare con la crescente complessità degli ordini decimali. In una delle attività proposte ai più piccoli (ultimo anno della Scuola dell'Infanzia) si lavora con successivi “impacchettamenti”, seguendo anche qui un percorso narrativo il cui protagonista è un piccolo egiziano che per catalogare il suo tesoro scopre i vari simboli numerici e il loro significato (Ahmose e i 999.999 lapislazzuli, S. Frasca ­ R. Petti ).
figura3
Un mucchio di piccoli oggetti (lapislazzuli nella storia, sassolini raccolti dai bambini o altre cose come chicchi, semi, pastina, piccole palline ... nei laboratori) vengono impacchettati dieci a dieci. Su ogni pacchetto si segna il simbolo geroglifico del dieci. Dieci pacchetti vengono raccolti in un piccolo sacchetto, contraddistinto da un nuovo simbolo, dieci sacchettini in un sacchetto grande, e così via. Lavorando con sacchetti e simboli numeri molto grandi diventano gestibili e facilmente confrontabili.
Anche nel sistema degli antichi cinesi si trova la forte presenza dell'oggetto materiale nella rappresentazione numerica. Qui si tratta di bastoncini che originariamente erano di bambù. Anche qui per la rappresentazione dei primi numeri si ne usano uno, due, tre, quattro o cinque messi vicini. Dal sei al nove invece un unico bastoncino, che si differenzia dagli altri perché diversamente orientato, prende il posto di cinque bastoncini “semplici”, e dunque i numeri si compongono come in figura (nelle due varianti, orizzontale o verticale). figura4
Rispetto ai sassolini sumeri, la disposizione nello spazio è qui molto più importante. Oltre ad avere un orientamento ben preciso, i bastoncini si vengono a disporre su tavole quadrettate. Alle unità è riservata la colonna più a destra. Se si vogliono rappresentare le decine si occupa la seconda colonna, subito a sinistra. E così si procede per centinaia, migliaia, ... .
Un aspetto interessante è che a questa rappresentazione materiale corrisponde una rappresentazione scritta. Su carta i segni dei numeri da uno a nove sono composti da aste che riproducono la disposizione dei bastoncini. La quadrettatura della tavola però sparisce e dunque è solo la posizione reciproca dei gruppi di bastoncini ad indicare a quale ordine decimale si debbano riferire. Si tratta dunque di una scrittura posizionale. Nel passaggio su carta c'è bisogno di indicare in qualche modo la presenza di una o più colonne che nella tavola fossero eventualmente vuote. Si introduce dunque un ulteriore segno, un tondo: ecco che si scopre una delle funzioni del nostro zero. I nove segni cinesi per i numeri da uno a nove, conservando uno stretto legame con i bastoncini, conservano un carattere operativo, che è assente dai nostri simboli. Se nella nostra notazione scriviamo ad esempio 7+2, la risposta, 9, è comprensibile solo a chi sia familiare con i simboli stessi e per essere trovata comporta più passaggi: dai simboli al loro significato, il calcolo, il ritorno dal significato al simbolo. L'addizione in sé è, in certo senso, nascosta dietro i simboli.
La stessa addizione espressa con i simboli cinesi risulta più immediata e comprensibile anche a chi per la prima volta veda questi simboli; il calcolo può avvenire direttamente in modo grafico. L'addizione in sé è subito visibile.
figura 5
I sassolini nelle tavole di conto ci riportano al “calculus” sumero. Come nel caso dei bastoncini cinesi la differenziazione dei valori viene determinata dalla posizione nello spazio artificiale della tavola che è suddiviso da righe verticali o orizzontali, a seconda del tipo. Nei laboratori utilizziamo generalmente il tipo a righe orizzontali, molto diffuso fino al tardo Medioevo nella contabilità. Per rendere più chiaro il confronto con altri strumenti, nelle considerazioni che seguono faremo però riferimento a tavole con righe verticali. Ad ogni colonna corrisponde un ordine decimale: i sassolini sulla colonna più a destra hanno valore unitario, quelli sulla seconda colonna valgono ciascuno una decina, quelli sulla terza un centinaio, e così via. Nel mondo classico e fino al Medioevo alla rappresentazione su tavola si affianca la rappresentazione scritta con, ad esempio, i numeri romani. A differenza di quanto accade con i bastoncini cinesi, il passaggio su carta non dà qui luogo a una scrittura posizionale. A ben vedere il fatto che strumenti analoghi come le tavole cinesi e le tavole di conto diano luogo a numerazioni di natura diversa, l'una posizionale e l'altra no, si riconduce al fatto che nella lettura delle tavole e nell'interpretazione della disposizione degli oggetti, sassolini o bastoncini, si privilegiano aspetti diversi. Nelle tavole di conto è la differente natura delle colonne a prevale, mentre nel sistema cinese è l'analogia. Nell'uso della tavola di conto infatti ogni sassolino viene trascritto con un diverso simbolo a seconda della colonna su cui trova; così due sassolini sulla colonna delle centinaia, uno su quella delle decine e due su quella delle unità, vengono trascritti come CCXII. Nella storia delle tavole di conto occidentali compare un tentativo anche nell'altra direzione ed è costituito dall'abaco di Gerberto; qui si contano i sassolini su ciascuna colonna e si sostituiscono con un solo gettone recante simboli (una variante delle cifre arabe occidentali) che corrispondono alle nostre cifre da 1 a 9. Questi simboli trascritti su carta condurrebbero proprio al nostro sistema posizionale, ma nella storia questa pratica rimane poco diffusa e non si svincola dall'uso della tavola. Bisognerà attendere ancora un paio di secoli perché la notazione posizionale con le cifre indo­arabiche si diffonda.
Il calcolo aritmetico
Proponiamo ora qualche osservazione su come i diversi modi di eseguire le operazioni mettano in evidenza diversi aspetti e difficoltà. Ci limitiamo a considerare come esempio qualche procedimento relativo alla moltiplicazione. I modi che richiamiamo vengono nei laboratori ovviamente proposti con modalità diverse a seconda che ci stia rivolgendo a bambini che stanno scoprendo la moltiplicazione o l'hanno da poco scoperta, o a ragazzi che magari hanno avuto modo di incontrare anche in contesti più ampi e più astratti diverse leggi di composizione. Un primo modo di moltiplicazione che si può considerare utilizzando i sassolini dei sumeri è quello di eseguire un'addizione ripetuta. Se ad esempio volessi moltiplicare un cono grande e due palline, cioè ottanta, per quattro dovrei prendere per quattro volte un cono grande e due palline. Il mucchietto di sassolini che ho ottenuto è il risultato cercato. Posso aver bisogno, come in questo caso, di aggiustarlo eseguendo dei cambi, in modo da rappresentarlo nella forma migliore. Qui dovrò sostituire sei palline con un cono grande, ottenendo cinque coni grandi e due palline.
Osserviamo che posso prendere per quattro volte un­cono­grande­e­due­palline oppure prendere per quattro volte un­cono­grande e prendere per quattro volte due­palline.
Quando moltiplico per numeri sempre più grandi il primo metodo diventa sempre meno praticabile. Se con pazienza riesco a ripetere il primo numero tante e tante volte senza perdere il conto mi trovo poi a gestire un enorme mucchio di sassolini su cui effettuare tanti cambi. Ecco allora delinearsi un secondo modo. La pratica del cambio mi suggerisce delle scorciatoie: se, ad esempio, devo moltiplicare per dieci, invece che ripetere sei coni dieci volte e solo poi sostituirli con una pallina, posso pensare di compiere un salto e sostituire direttamente con un cono piccolo con una pallina; posso formalmente dire che un cono piccolo per una pallina (che mi tiene il conto delle dieci volte per cui devo moltiplicare) vale una pallina; in modo analogo posso ad esempio formalmente dire che un cono grande per una pallina (dieci) vale un cono grande bucato. In questo modo se devo moltiplicare sessantadue per dieci, cioè un­cono­grande­e­due­coni­piccoli per una pallina, ottengo un­cono­grande­col­buco­e­due­palline. Una volta trovate relazioni analoghe tra tutti i diversi calculi (cioè costruendo una tabella di moltiplicazioni tra i simboli sumeri) posso eseguire una moltiplicazione aiutandomi con una tabella a doppia entrata dove pongo i sassolini dei due numeri da moltiplicare che e riempio secondo i prodotti semplici che ho trovato. Per l'additività della notazione, sto usando la proprietà distributiva sui simboli sumeri. Figura6
didascalia: due­coni­grandi­bucati­un­cono­grande­quattro­coni­piccoli moltiplicati per centoventuno, cioè due­coni­grandi­e­un­cono­piccolo
La matematica degli antichi egizi permette di sperimentare un altro modo per accorciare l'addizione ripetuta. Invece di sommare secondo il numero di volte dato, si calcolano i raddoppi successivi di uno dei due numeri da moltiplicare; se ne sommano poi alcuni, scegliendoli in base al secondo dei due fattori. In definitiva sto usando ancora la proprietà distributiva, ma questa volta il secondo fattore, che rimane nascosto, viene scomposto in somma di potenze di due. figura7
Il fatto che addizione e sottrazione, moltiplicazione e divisione, siano operazioni inverse una dell'altra traspare in modo più o meno evidente nei diversi metodi di calcolo.
La somma con i calculi sumeri si esegue unendo un mucchietto di sassolini all'altro. La sottrazione togliendo un mucchietto di sassolini da uno dato. Se immaginiamo di vedere un filmato dell'addizione e poi di proiettarlo al contrario vederemo una sottrazione. Lo stesso vale per addizione e sottrazione sulle tavole di conto o con i bastoncini cinesi. Nel nostro calcolo scritto non si ha questa immediata corrispondenza, anche se nell'eseguire una sottrazione e l'addizione sua inversa si percepisce bene che si sta in qualche modo tornando indietro.
Più nascosto ancora è il caso moltiplicazione­divisione. Il nostro algoritmo della divisione è a prima vista piuttosto lontano da quello della moltiplicazione. Nel procedimento egizio invece il legame appare in modo evidente. Per eseguire la divisione si usa infatti lo stesso schema della moltiplicazione ma letto ora da destra a sinistra, cioè nella colonna di destra, con i raddoppi del divisore (primo fattore), si cerca il dividendo (prodotto) e poi a sinistra, tra i raddoppi dell'unità, si forma corrispondentemente il risultato (secondo fattore).
figura8
Da qui ancora qualche spunto per riflettere sulla moltiplicazione. Il metodo egizio si può riformulare considerando le potenze del dieci invece di quelle del due. Nello schema allora compaiono i multipli secondo dieci del primo fattore; ognuno si dovrà ora prendere una, due, ..., nove o zero volte, in base a quanto indica il secondo fattore. Nello schema allora si ritrovano i passaggi del nostro algoritmo. Nello stesso schema si ritrovano i passaggi della divisione.
Il tentativo di rendere sempre più semplice il calcolo porta all'ideazione di strumenti che riducano l'intervento di chi deve trovare il risultato. Alcuni esempi si possono sperimentare nel laboratorio dedicato ai regoli per eseguire moltiplicazioni, divisioni e estrazione di radici. Si tratta dei bastoncini di Nepero e di alcune loro varianti con cui, riducendo o eliminando, del tutto i conteggi si trovano immediatamente i risultati. Il loro utilizzo è semplice, tanto più semplice quanto più lo strumento si fa sofisticato. La difficoltà si sposta allora adesso nella costruzione dello strumento e nel tirare fuori la matematica che vi si nasconde. Biblio/sitografia
Il Giardino di Archimede – Un Museo per la Matematica
­ pagina principale www.archimede.ms
­ le mostre: http://php.math.unifi.it/archimede/archimede/esposizioni.php
­ i laboratori: http://php.math.unifi.it/archimede/archimede/laboratori/offertadidattica.php
Ifrah Georges, 1983, Storia universale dei numeri, Mondadori
Frasca Simone, Petti Raffaella, 2008, Uri, il piccolo sumero, Il Giardino di Archimede – Un Museo per la Matematica
Frasca Simone, Petti Raffaella, 2008, Ahmose e i 999.999 lapislazzuli, Il Giardino di Archimede – Un Museo per la Matematica
Torino, 27 gennaio 2011