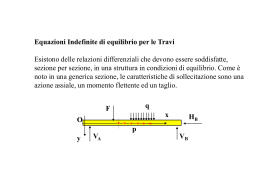
Lezione n. 2
Le lastre piane inflesse
La soluzione del problema elastico
Lastra illimitata in una direzione
Come prima applicazione delle equazioni scritte in precedenza, si consideri il caso di una lastra illimitata in una direzione (supposta coincidente con la direzione X), vincolata uniformemente lungo
i lati lunghi (ad esempio, con un vincolo di appoggio fisso) e sottoposta all’azione di un carico distribuito uniforme p.
X
b
Y
f
p
1
Dato il particolare problema affrontato, si può osservare che ogni linea parallela all’asse Y rappresenta un asse di simmetria del problema; di conseguenza, la soluzione della lastra, in termini di spostamenti, dovrà risultare indipendente dalla coordinata x. Si ha cioè
w  x, y   w  y 
Questo fatto risulta vero anche se il carico non è uniforme ma dipendente solo da y.
Come conseguenza diretta si ottengono le seguenti espressioni per i momenti flettenti e torcenti
lungo la lastra:
 2w
2w 
d2w
m X  B   2    2   m X   B    2    m Y
y 
dy
 x
 2w
2w 
d2w
m Y  B   2    2   m Y   B  2
x 
dy
 y
 2w 
m XY  B  1     
  m XY  0

x

y


quindi non nascono momenti torcenti (come è ovvio, visto che tutte le fibre in direzione Y ruotano
in misura indipendente da X) mentre i momenti in direzione longitudinale (X) sono semplicemente
una frazione (attraverso il coefficiente di Poisson ν) dei momenti nell’altra direzione. La particolare
conformazione della deformata della lastra viene definita come “deformata cilindrica” in quanto le
rette lungo X (che si mantengono rettilinee anche a seguito della deformazione) corrispondono, in
configurazione deformata, alle generatrici di un cilindro retto.
I momenti flettenti che nascono in direzione trasversale, sono gli stessi che nascerebbero in una
trave di uguale lunghezza b, sottoposta ad un carico uniformemente distribuito e vincolata come i
lati lunghi della piastra. L’equazione di Germain-Lagrange diviene infatti, in questo caso,
4w
4w
4w p
d4w p

2




x 4
x 2 y 2 y 4 B
dy 4 B
Gianni Bartoli/Claudio Mannini/Carlo Guastini – Appunti di Tecnica delle Costruzioni (2)
Revisione – 28/05/12
Lezione n. 2 – pag. II.2
che corrisponde alla usuale equazione della linea elastica, dove si sostituisca al termine EJ il termine B. Quindi i momenti flettenti sono gli stessi di una trave di larghezza unitaria (dal momento che
non dipendono da EJ, o da B, se tali caratteristiche sono uniformi in direzione trasversale), mentre
le deformazioni sono ridotte, in quanto la trave equivalente risulta leggermente più rigida a causa
della presenza in B del termine E/(1-ν2) anziché del solo modulo di Young E.
Si può quindi procedere al calcolo isolando una striscia di larghezza unitaria, ottenendo, nel caso in
esame
p  b2
m Y,max 
8
5 p  b4
5
p  b4
f  w max 

384 B
384  E  s3


2 
 1    12
Occorre infine ricordarsi di considerare la presenza dell’ulteriore momento flettente in direzione X,
pari a ν volte il momento in direzione Y e costante lungo linee parallele all’asse X.
La presenza di tale momento flettente ed il suo valore sono facilmente intuibili se si pensa alla deformazione che una trave inflessa subisce trasversalmente alle fibre longitudinali; infatti la sezione
di larghezza 1 ed altezza s, oltre ad abbassarsi della quantità w, subisce la deformazione mostrata in
figura a causa della presenza di un valore diverso da zero del coefficiente di contrazione laterale ν.
Pensando ad un momento con segno positivo, le fibre di estradosso (compresse in direzione Y) tendono a deformarsi in direzione X (la deformazione vale ν·ε Y), mentre nelle fibre di intradosso avviene lo stesso fenomeno con segno opposto. Dal momento che tale deformazione è impedita dalle
strisce adiacenti (che dovrebbero a loro volta deformarsi secondo la stessa modalità), è evidente che
devono nascere delle tensioni trasversali σX (= ν·σY) che annullano tale deformazione; la distribuzione di tensioni necessaria a ripristinare la congruenza deformativa tra strisce adiacenti è quella
causata da un momento flettente trasversale, di entità appunto pari a m X = ν·mY. È altresì evidente
che tale momento flettente ha lo stesso segno del momento m Y che lo ha provocato, e quindi tende
le stesse fibre tese a causa del momento mY.
1
s
w
1+εY
σX
X
mX
Z
mX mX
mX
Alla luce delle considerazioni riportate, nel caso in cui un elemento in c.a. a comportamento bidimensionale venga progettato con riferimento ad una striscia isolata di larghezza arbitraria (come è il
caso, ad esempio, di un solaio o di un muro di sostegno), è opportuno che in direzione ortogonale a
quella del calcolo venga sempre prevista un’armatura trasversale di entità pari almeno a ν volte
quella disposta nella direzione principale, al fine di assorbire il momento trasversale che il comportamento a piastra fa insorgere1.
1
Tale prescrizione era esplicitamente riportata in alcune delle normative precedenti a quella attuale. A titolo di esempio, nel DM 9.1.1996, nel capitolo riguardante i solai, era espressamente riportato che “per i solai con nervatura gettata o completata in opera (…) quando sia sensibile il comportamento a piastra (…)” si deve prevedere un’adeguata
armatura nelle solette almeno pari “al 20% di quella longitudinale nell’intradosso del solaio”; è evidente che tale
indicazione discende dall’osservazione effettuata in precedenza, se si riconosce alla percentuale del 20% il ruolo offerto da un coefficiente di Poisson pari a 0.2.
Gianni Bartoli/Claudio Mannini/Carlo Guastini – Appunti di Tecnica delle Costruzioni (2)
Revisione – 28/05/12
Lezione n. 2 – pag. II.3
Alla luce delle considerazioni appena fatte, è facile capire perché il comportamento bidimensionale
comporti una rigidezza flessionale maggiore (di un fattore 1/(1-ν2)) rispetto al caso monodimensionale, come visto nella lezione precedente. Infatti, presa la stessa striscia di larghezza unitaria, spessore s e lunghezza b, pensandola isolata dalle altre, la sua curvatura è data da:
M
Y  3Y
Es 1
Il momento mX = ν·mY, necessario per ristabilire la congruenza trasversale fra le strisce, sempre per
effetto Poisson, produce in direzione Y una curvatura pari a:
M
Y   3 X
Es 1
Il segno negativo dipende dal fatto che le fibre compresse trasversalmente da m X si allungano in
direzione longitudinale, mentre si accorciano quelle tese. La curvatura complessiva risulterà pari a:
1  2   MY  MY
M
M
 Y   Y   Y  3Y  3 X 
E 3
Es 1 Es 1
Es3 1
s 1
1  2
Come verrà mostrato nel seguito, una lastra molto allungata (con un rapporto fra i lati superiore a
cinque o anche meno, se si accetta un’approssimazione un po’ maggiore) si comporta sostanzialmente come quella illimitata, fatta eccezione per la zona in prossimità dei lati minori, dove la soluzione dipende dal tipo di vincolo effettivamente presente. Tale soluzione è disponibile in letteratura
ma è tuttavia interessante fare alcune semplici osservazioni. Nel caso di lato minore incastrato, il
momento flettente mX assume un valore negativo pari in modulo a quello massimo mY nella zona a
deformata cilindrica. Se il bordo minore è appoggiato, le reazioni vincolari verticali raggiungono in
mezzeria un valore massimo appena superiore a quello che si ha sui lati maggiori. Se il bordo è libero, gli abbassamenti risultano leggermente superiori rispetto alla zona corrente, tanto più quanto
maggiore è il coefficiente di Poisson. Inoltre, nei casi di bordo libero e appoggiato, nasceranno delle
reazioni concentrate in corrispondenza degli spigoli (cfr. sezione successiva). Infine, in prossimità
dei lati minori non saranno più nulli i momenti torcenti.
Le condizioni al contorno: il taglio di Kirchhoff (taglio di sostituzione)
L’integrazione dell’equazione di Germain-Lagrange richiede la definizione delle condizioni al contorno. Le condizioni di vincolo per le lastre inflesse sono normalmente costanti lungo lo sviluppo di
ciascun bordo e sono costituite da condizioni di bordo incastrato, appoggiato o libero (assenza di
vincoli).
La prima condizione impone lungo lo sviluppo di tale bordo l’assenza di spostamenti verticali e
rotazioni con asse parallelo al bordo. Considerando, a titolo di esempio, che il bordo in esame si
sviluppi lungo X (quindi abbia equazione del tipo y = c), le condizioni al contorno possono quindi
essere scritte come
 w y c  0


w
0
X yc   x
y c

È da notare che, implicitamente, si è anche affermato che, lungo tale bordo, non si abbiano rotazioni
in direzione Y, in quanto la prima condizione porta ovviamente a
Nell’EC2 le raccomandazione è ancora presente, in quanto si indica che “nelle piastre a portanza unidirezionale si
raccomanda di prevedere una armatura trasversale secondaria in quantità non minore del 20% dell’armatura principale” (UNI-ENV 1992-1-1:2005 “Eurocode 2: Design of concrete structures – Part 1-1: General – Common rules for
building and civil engineering structures”, p.to 9.3.1.1).
Gianni Bartoli/Claudio Mannini/Carlo Guastini – Appunti di Tecnica delle Costruzioni (2)
Revisione – 28/05/12
Lezione n. 2 – pag. II.4
Y
y c

w
y
0
y c
Nel caso di bordo appoggiato, le condizioni da imporre riguardano l’assenza di spostamenti verticale e l’uguaglianza del valore del momento flettente all’eventuale momento m f applicato. Di conseguenza occorre scrivere (considerando sempre il vincolo lungo il bordo y = c)

 w y c  0


 2w

2w 
m


B




 mf

 X y c
2 
 x 2


y



y c
Il valore identicamente nullo dello spostamento w lungo y = c consente di affermare che risulta nulla la derivata ∂2w/∂y2 e quindi di riscrivere le condizioni precedenti come

 w y c  0


 2w 

m


B

 mf
 2 
 X y c

x


y c

Ovviamente, nel caso in cui non ci siano coppie applicate lungo il bordo, occorrerà porre uguale a
zero il valore della corrispondente caratteristica di sollecitazione.
Infine, nel caso di bordo libero, occorrerà imporre lungo lo sviluppo di tale bordo l’uguaglianza dei
valori delle forze e delle coppie applicate ai corrispondenti valori delle caratteristiche di sollecitazione

 3w
3w 
q X


B


t
 3
2 

 y c

x

x

y

 y c


 2w
2w 

 mf
m X yc  B   2    2 
y  yc
 x


 2w 

m


B

1



 mt




 XY yc

x

y



y c
Emerge quindi un’anomalia nelle condizioni scritte in quest’ultimo caso: mentre per i bordi incastrato ed appoggiato si sono imposte due sole condizioni, per il bordo libero sembrerebbe necessario
imporre tre diverse condizioni al contorno lungo il lato in esame.
In realtà, si deve a Kirchhoff la dimostrazione di come la prima e la terza equazione possano essere
inglobate in un’unica condizione al contorno, in quanto, in luogo di tali due condizioni, occorre
imporre che

m t
m XY 
 t X 
  t 
y  yc
y

e quindi
 3w
  3 w 
m t

 B   3  2     
t
2 
y
 x y  yc
 x
In pratica, nell’equazione precedente si è introdotto sul bordo libero una distribuzione di azioni taglianti equivalenti del tipo
Gianni Bartoli/Claudio Mannini/Carlo Guastini – Appunti di Tecnica delle Costruzioni (2)
Revisione – 28/05/12
Lezione n. 2 – pag. II.5
m XY
y
che rappresenta la variazione del momento torcente. Tale grandezza, che prende il nome di “taglio
di sostituzione”, è stata introdotta da Kirchhoff (1850), dimostrando la validità dell’uguaglianza
attraverso una procedura di tipo variazionale; da un punto di vista fisico, essa corrisponde al fatto di
avere imposto la conservazione della sezione piana, di fatto riducendo il numero di gradi di libertà
della piastra2.
Alla dimostrazione di Kirchhoff se ne può aggiungere un’altra, dovuta a Thomspon e Tait (1867).
Al momento torcente applicato sul bordo
della lastra, per il principio di De Saint Venant, si può sostituire una distribuzione di
tante forze verticali, uguali ed opposte, che
danno luogo a coppie; considerando ad
esempio un tratto di bordo di larghezza dy
Y
X
(corrispondente alla porzione terminale di
mYX·dy
mXY·dx
una fibra disposta lungo Y), uguagliando il
Z
valore del momento torcente a quello prody
dx
vocato dalle due forze VX, anch’esse a diX
stanza dy, si avrebbe
dy
dx
Y
dx
VX  dy  mXY  dy
dy
dy
dx
e quindi
t *X 
VX  mXY
Y
VY = mYX
Nella striscia adiacente, dove il momento
risulta
incrementato
della
quantità
(∂mXY/∂y)·dy, la forza VX aumenta della
quantità dVX, per cui si ottiene
X
VX = mXY

Z
dy
dx
dy
2
X
Y
dy
dy

 VX  dVX   dy   mXY 
dx
dx
VX 

mXY
 dy   dy
y

dVX
mXY
 dy  mXY 
 dy
dy
y
In corrispondenza del confine tra le due
strisce, i due contributi VX si annullano, per
cui rimane il solo contributo
dx
R = 2·mXY
La circostanza è simile a quella che si verifica in una trave inflessa sottoposta ad una distribuzione uniforme di coppie
flettenti. L’equilibrio fornisce:
m
R L  mL  R  m
e quindi il taglio ed il momento flettente lungo la trave valgono
V z  R
L
R
R
M  z   R  z  m  z  0
quindi la trave è soggetta ad un momento flettente nullo e ad un taglio costante pari al valore del momento applicato.
Se si trascurano le deformazioni per taglio, la trave rimane indeformata. Soltanto eventuali distribuzioni non uniformi
di coppie flettenti lungo lo sviluppo della trave producono un momento flettente, anch’esso variabile lungo l’asse della trave, in funzione del valore di dm/dz.
Gianni Bartoli/Claudio Mannini/Carlo Guastini – Appunti di Tecnica delle Costruzioni (2)
Revisione – 28/05/12
Lezione n. 2 – pag. II.6
mXY
 dy
y
relativo ad una larghezza dy; quindi, l’azione tagliante unitaria si ottiene dividendo l’espressione
precedente per dy, ossia
dV
mXY
t *X  X 
dy
y
dVX 
che rappresenta un’azione di taglio che va ad aggiungersi all’eventuale forza per unità di lunghezza
t applicata sul contorno. Tale azione, sostituendosi al momento torcente, viene indicata con la denominazione di “taglio di sostituzione”. In corrispondenza degli spigoli della lastra, in cui si ha un
cambio di direzione della normale al contorno, i due contributi provenienti dalle strisce di diversa
orientazione non si annullano a vicenda; se l’angolo è retto, nasce quindi un’azione concentrata di
entità pari al doppio del valore del momento torcente
R  2  mXY
I momenti principali
Come si è notato, nelle lastre inflesse esiste un collegamento diretto e biunivoco tra tensioni e caratteristiche di sollecitazione.
Di conseguenza, limitando l’attenzione ai soli momenti m X, mY e mXY = mYX, si può costruire, in
ogni porzione della lastra, un tensore che è direttamente derivato dalla parte del tensore delle tensioni con risultante nulla sullo spessore:
mXY 
 X XY 
m
  X



 YX Y 
 mYX mY 
Il legame precedente va interpretato nel senso che alla presenza delle componenti del tensore delle
tensioni di sinistra corrispondono necessariamente i valori dei momenti contenuti nella matrice di
destra.
Se in un punto, e per una particolare giacitura, il tensore delle tensioni assume una forma diagonale
(si annullano cioè gli elementi extra-diagonali del tensore), anche la matrice che individua localmente il tensore dei momenti dovrà assumere la stessa forma
I 0 
mI 0 
0     0 m 

II 

II 
Ai due valori dei momenti mI e mII (analogament
α
te a quanto fatto per le tensioni) si dà il nome di
n
X
momenti principali; quindi, lungo le direzioni
principali, in cui si hanno soltanto tensioni normali, sono presenti soltanto sollecitazioni flesn
Y
sionali (e non sollecitazioni torcenti).
α
mnt
Valgono inoltre, per i momenti flettenti principamn
s
li, le stesse proprietà delle tensioni principali; in
t
particolare, i momenti mI e mII rappresentano i
X
valori estremi (massimo e minimo) dei momenti
mXY mX
flettenti tra tutte le possibili giaciture in un punto.
Y
mY
mXY
Ricordando le espressioni valide per le tensioni principali, si possono ricavare i valori dei momenti
principali e dell’angolo ϑ di inclinazione delle direzioni principali rispetto all’asse X attraverso le
usuali relazioni. Ricavando i valori del momento flettente e torcente rispetto ad una generica giacitura inclinata di un angolo α rispetto all’asse X, si ottiene
Gianni Bartoli/Claudio Mannini/Carlo Guastini – Appunti di Tecnica delle Costruzioni (2)
Revisione – 28/05/12
Lezione n. 2 – pag. II.7
m n  m X  cos 2   m Y  sin 2   m XY  sin  2 


1
m nt    m X  m Y   sin  2   m XY  cos  2 

2
e quindi, ricercando la direzione ϑ lungo la quale il valore del momento torcente m nt è nullo, si ottengono le relazioni
mI  mX  mY 1
 

mII 
2
2
 mX  mY 
2
tg  2 
 4  m2XY
2  m XY
mX  mY
È interessante osservare un’altra proprietà dei momenti torcenti lungo la lastra: essi forniscono localmente una misura di quanto le direzioni principali si discostano dalle direzioni X ed Y. Tanto
maggiore (in valore assoluto) è il valore del momento torcente, quanto più le direzioni principali
non coincidono con X ed Y. Questa osservazione è particolarmente rilevante nel caso di lastre inflesse in c.a.: dal momento che le armature dovrebbero assorbire le trazioni provocate dai momenti
flettenti agenti sulla lastra, le direzioni principali rappresentano le direzioni “privilegiate” lungo le
quali tali armature andrebbero possibilmente disposte.
La soluzione della lastra quadrata uniformemente caricata
La soluzione per la lastra inflessa quadrata soggetta a carico uniforme è stata ricavata da Navier
(1820) sotto forma di serie trigonometriche doppie, e successivamente da Lévy (1899) e Nadai
(1915) in forma di serie trigonometriche semplici.
A parte alcuni valori della soluzione in punti specifici della lastra, che verranno introdotti successivamente, alcune caratteristiche di questa si prestano a considerazioni di carattere generale, per cui
vale la pena soffermarcisi.
X
0, 46  p  a
qY
p  a 2  1   
27,14
mII
C
a
mY
mI
mX
mXY
p  a 2  1   
21, 6
p  a 2  1   
27,14
II
A
mYX
d
d
C
a
p  a 2  1   
21, 6
I
X
Y
a
p  a 2  1   
21, 6
Y
A
a
Simmetrie: sotto l’azione di un carico uniforme, la lastra possiede diversi assi di simmetria, offerti
dalle due rette passanti per il centro C e parallele ai lati e dalle diagonali. Tali assi sono principali
per i momenti flettenti, dovendo essere nullo, lungo tali direzioni, il valore del momento torcente
per considerazioni di simmetria. Ovviamente, sempre a causa delle simmetrie, l’andamento dei
momenti flettenti mX lungo la striscia parallela all’asse X e passante per C è uguale
all’andamento dei momenti flettenti m Y lungo la striscia parallela ad Y ed ancora passante per il
centro C (la doppia simmetria della struttura implica che i due assi X ed Y possano essere scambiati tra loro senza modificare la soluzione della struttura).
Punto C: come già osservato, siamo in una condizione caratterizzata dalla presenza di momenti flettenti uguali nelle due direzioni X e Y e dall’assenza di momenti torcenti. Tale circostanza fa degenerare il circolo di Mohr (attraverso il quale sarebbe possibile individuare le direzioni principali) ad un punto; di conseguenza, tutti gli assi passanti per C sono in C direzioni principali ed i
Gianni Bartoli/Claudio Mannini/Carlo Guastini – Appunti di Tecnica delle Costruzioni (2)
Revisione – 28/05/12
Lezione n. 2 – pag. II.8
momenti flettenti assumono quindi lo stesso valore lungo qualunque giacitura. Il valore del momento flettente in C, ricavato attraverso sviluppi in serie della soluzione, è pari a
p  a 2  1   
16  0, 224
2
mC  mX,C  mY,C 
 p  a  1    
4
27,14
mentre il valore fC della freccia nel punto C è pari a
16  0, 244 p  a 4
1 p  a4
fC 



6
B
246 B
È interessante notare che, considerando ν = 0, tali valori coincidono, a meno di un fattore pari
circa a π, con quelli di una trave appoggiata di sezione s·1, sottoposta allo stesso carico p:
1 5 p a4
1 p  a2
fC  

mC  
s3
 384
 8
E
12
Andamento del momento torcente lungo i bordi appoggiati: analizzando il bordo che parte dallo
spigolo A e si sviluppa in direzione X, è facilmente intuibile che le strisce che si sviluppano verso Y avranno rotazioni φY via via sempre maggiori, a causa del diverso sostentamento offerto
dalle strisce in direzione ortogonale. La rotazione φ Y tende ad assumere il suo valore massimo in
corrispondenza della mezzeria del lato, per poi decrescere fino ad un valore nullo in corrispondenza dello spigolo opposto (allo spigolo la rotazione è nulla per la presenza del vincolo di appoggio in direzione Y). Collegando il valore del momento torcente alla variazione lungo X della
rotazione φY
 2w 
  w 

mYX  B  1     
  B  1      
  B  1      Y 
x  y 
x
 x y 
è evidente quindi che lo stesso avrà un andamento antisimmetrico, essendo positivo nella prima
parte (fino alla metà del lato), annullandosi in corrispondenza della mezzeria del lato (dove, come già evidenziato, è presente un asse di simmetria) e negativo nella restante parte. L’andamento
effettivo è riportato in figura, dove si nota che il massimo del momento torcente si raggiunge in
corrispondenza dello spigolo, dove assume il valore
p  a 2  1   
mXY,A  mYX,A 
21, 6
Come già osservato in precedenza, tale distribuzione dei momenti torcenti lungo il lato corrisponde alla presenza di ulteriori reazioni verticali di appoggio causate dalla variazione del momento torcente lungo lo sviluppo X del lato, di valore pari a
m YX
t *Y 
x
Infine, le stesse osservazioni appena fatte per il lato lungo X valgono anche per gli altri lati appoggiati, stante la simmetria del sistema analizzato.
Spigolo A: nello spigolo A i momenti flettenti m X e mY sono nulli (il vincolo di appoggio per le
strisce che si sviluppano lungo X consente la rotazione φX e quindi rende nullo il momento m X;
analogamente per le strisce lungo Y, la rotazione φ Y, consentita, corrisponde ad annullare il momento mY)3; sono invece presenti momenti torcenti di valore pari a quello indicato in precedenza. Se si ricercano le direzioni principali, si può quindi osservare (sia attraverso le espressioni
analitiche, sia attraverso i circoli di Mohr, che delle espressioni analitiche sono la rappresenta-
3
Di fatto, lo spigolo offre un incastro alla piastra, in quanto la presenza contemporanea di vincoli di appoggio in entrambe le direzioni impedisce sia le rotazioni φ X che le rotazioni φY. In ogni altra direzione diversa da X e Y, la rotazione è ancora nulla, potendo evidentemente essere sempre scomposta in una componente lungo X ed una lungo Y,
entrambe necessariamente nulle.
Gianni Bartoli/Claudio Mannini/Carlo Guastini – Appunti di Tecnica delle Costruzioni (2)
Revisione – 28/05/12
Lezione n. 2 – pag. II.9
zione grafica) che queste sono orientate a ±45° rispetto all’asse X e che i momenti corrispondenti
assumono i valori
mI  mII  mXY 
p  a 2  1   
21, 6
In particolare, lungo la diagonale u, il momento flettente m u assume il valore mII (negativo),
mentre in direzione ortogonale (v) il momento flettente è positivo. Analizzando l’andamento del
momento flettente lungo la diagonale u, si nota quindi che questo parte da un valore negativo,
assume un valore positivo in mezzeria (dove anche u è direzione principale, per cui il momento
vale mC), per poi tornare ad un valore negativo allo spigolo opposto. L’andamento del momento
flettente non è quindi dissimile da quello di una trave incastrata agli estremi, anche se con valori
ridotti a causa del comportamento bidimensionale della lastra. È infine utile notare come il momento flettente in corrispondenza dello spigolo è, per gli usuali valori di ν, maggiore, in valore
assoluto, del valore che si ottiene in mezzeria.
Nel caso di lastre inflesse in c.a., quindi, la disposizione ottimale dei ferri richiederebbe, in corrispondenza degli spigoli, un’armatura superiore disposta lungo la diagonale (dove il momento,
come già detto, assume valori negativi) e un’armatura inferiore disposta in direzione ortogonale
alla diagonale.
Un’ultima osservazione, che discende dall’interpretazione delle variazioni di momento torcente
come tagli di sostituzione, riguarda la presenza di una reazione concentrata presente nello spigolo della lastra. I momenti torcenti derivanti dalle due direzioni ortogonali X e Y comportano, nello spigolo, la presenza di un’azione rivolta verso l’alto di valore pari a
p  a 2  1   
VA  2  m XY,A 
10,8
che richiede quindi la realizzazione di un vincolo bilatero per impedirne il sollevamento.
Soluzione nel caso di lastra rettangolare: nel caso di lastra rettangolare (di lati a e b), ancora appoggiata sul contorno e sottoposta all’azione di un carico uniforme, è possibile ricorrere a soluzioni
tabulate che esprimono, per diversi valori di ν e del rapporto b/a, i valori dei momenti flettenti in
alcune posizioni di interesse. A titolo di esempio, nel grafico successivo sono riportati i valori
dei momenti flettenti al centro della lastra relativamente al caso ν = 0,3; è interessante notare
che, già per valori del rapporto b/a poco superiori a 2, la soluzione si discosta in misura molto
limitata dalla soluzione che si avrebbe per rapporto dei lati b/a →∞, ossia dalla soluzione per lastra illimitata in una direzione.
a
X
mY
b
mX
Y
p  a2

p  a2


m X,C 
m Y,C
Valori dei momenti flettenti al centro della lastra (ν = 0,3) al variare del rapporto tra i lati
(i valori asintotici sono rappresentati da α = 8, β = 8/ν = 26.67)
Gianni Bartoli/Claudio Mannini/Carlo Guastini – Appunti di Tecnica delle Costruzioni (2)
Revisione – 28/05/12