CRITTOLOGIA CLASSICA e CRITTOLOGIA
MODERNA
a confronto
di
Caterina Urban
Udine, Liceo Scientifico “G. Marinelli”
a.s. 2005/2006
CHE COS’E’ LA CRITTOLOGIA?
• dal greco kryptos, “nascosto”, e logos, “discorso, parola”
• disciplina nata come branca della matematica e dell’informatica
• racchiude CRITTOGRAFIA e CRITTOANALISI
•
CHE COS’E’ LA CRITTOGRAFIA?
• dal greco kryptos, “nascosto” e graphein, “scrivere”
• si occupa dell’ideazione di metodi (sistemi cifranti) sempre più sicuri
per occultare un messaggio e renderlo incomprensibile a persone non
autorizzate
•
CHE COS’E’ LA CRITTOANALISI?
• si occupa dello studio e della comprensione delle informazioni
crittografate attraverso la rottura non autorizzata dei sistemi cifranti
• si distinguono crittoanalisi STATISTICA e crittoanalisi DIFFERENZIALE
CRITTOANALISI STATISTICA
analisi della frequenza
delle varie lettere del
primo capitolo de “I
Promessi Sposi” di
Alessandro Manzoni
analisi della frequenza delle varie lettere
del primo capitolo del “Frankenstein” di
Mary Shelley
analisi della frequenza delle varie
lettere dei primi 19 paragrafi del
terzo capitolo del “De Bello Gallico”
di Giulio Cesare
PRINCIPIO DI KERCKHOFFS
1883, La Criptographie Militaire
“la sicurezza di un crittosistema non deve
dipendere dalla segretezza dell’algoritmo usato,
ma solo dalla segretezza della chiave”
(principio o legge di Kerckhoffs)
Auguste Kerckhoffs
1949, Communication Theory of Secrecy
Systems
“il nemico conosce il sistema”
(massima di Shannon)
Claude Shannon
CRITTOGRAFIA SIMMETRICA
• crittografia CLASSICA (dall’antichità fino al 1975)
• chiave unica per le operazioni di cifratura e decifratura
PREGI:
• velocità
DIFETTI:
• problema della comunicazione della chiave
IL CIFRARIO DI CESARE
(cifrario MONOALFABETICO)
ESEMPIO:
Giulio Cesare
Svetonio (70/75-126 d.C.) in Le Vite dei Dodici Cesari (circa 120 d.C.):
..”..extant et ad Ciceronem, item ad familiares domesticis de rebus, in quibud, si qua occultius
preferenda erant, per notas scripsit, id est sic structo litterarum ordine, ut nullum verbum effici
posset: quae si qui investigare et persequi velit, quartam elementorum litteram, id est D pro A
et perinde reliquas commutet..”..
..”..restano quelle [le lettere] a Cicerone, così come quelle ai familiari sugli affari domestici,
nelle quali, se doveva fare delle comunicazioni segrete, le scriveva in codice, cioè con l’ordine
delle lettere così disposto che nessuna parola potesse essere ricostruita: se qualcuno avesse
voluto capire il senso e decifrare, avrebbe dovuto cambiare la quarta lettera degli elementi,
cioè D per A e così via per le rimanenti..”..
CIFRARIO DI VIGENERE
(cifrario POLIALFABETICO, XVI secolo)
Blaise de Vigenere
ESEMPIO:
..la singola lettera del testo
in chiaro non è sempre
cifrata con la stessa lettere
e questo rende più difficile
la crittoanalisi statistica del
testo cifrato!
tavola di Vigenere
DISCO CIFRANTE di ALBERTI
(cifrario POLIALFABETICO, 1400)
Leon Battista Alberti
• disco esterno stabile con 24
caselle contenenti 20 lettere
latine maiuscole in ordine
alfabetico (escluse H,K,W e Y
con U=VI=J) ed i numeri 1,2,3,4
per il testo in chiaro
• disco interno mobile con le 24
lettere latine minuscole messe
in disordine per il testo cifrato
La MACCHINA ENIGMA
•
VERSIONE DI BASE:
34 x 28 x 15 cm
12 Kg di peso
Arthur Scherbius
ELEMENTI PRINCIPALI:
•
ROTORI (o SCAMBIATORI): ognuno dei tre dischi rotanti
poteva orientarsi in 26 modi nel piano perpendicolare al
suo asse di rotazione (erano ammesse perciò
26*26*26=17.576 combinazioni di orientamenti)
•
UNITA’ CIFRATRICE: i tre rotori (1,2,3) potevano essere
inseriti nell’unità centrale in diverse posizioni
reciproche (erano quindi ammesse 6 diverse posizioni)
•
PANNELLO A PRESE MULTIPLE: 6 cavi muniti di
spinotti permettevano ognuno di scambiare due lettere
prima della loro immissione nel rotore (per un totale di
100.391.791.500 possibili abbinamenti!!)
•
RIFLESSORE
 il numero totale di chiavi possibili risulta essere circa 10 milioni di miliardi!
MARIAN REJEWSKI
8 Novembre 1931, Hans-Thilo Schmidt (Asche)
incontra un agente francese (Rex) e gli permette di
fotografare due manuali di istruzioni per la
cifratrice che rendevano possibile la costruzione
di una copia della macchina Enigma
Hans-Thilo Schmidt
Marian Rejewski
• sfrutta la ripetizione della chiave di messaggio a partire dalla quale individua
particolari relazioni tra le lettere
•a partire dalle relazioni individuate riesce a costruire particolari concatenazioni e
relativi collegamenti
• concatenazioni e collegamenti costituiscono le “impronte digitali” (grazie al
tradimento di Asche) dell’assetto degli scambiatori della chiave giornaliera di Enigma
• costruisce delle particolari macchine in grado di controllare meccanicamente gli
assetti (bombe di Rejewski)
ALAN TURING
Nasce a Londra, il 23 Giugno 1912.
Nel 1931 viene ammesso al King’s College dell’Università di Cambridge. Vi
giunge in un periodo di vivace dibattito sulla natura della matematica e
della logica; l’argomento più discusso era quello dell’ “indecidibilità”, una
nozione sviluppata dal logico Kurt Gödel.
Alan Turing
Nel 1937, pubblica l’articolo On Computable Numbers dove descrive per la
prima volta quella che poi verrà definita come la macchina di Turing.
Il 4 Settembre 1939, la Scuola Governativa di Codici e Cifre lo invitò a Bletchley Park come
crittanalista. Era necessario escogitare un nuovo procedimento per decifrare Enigma che non
dipendesse dalla ripetizione della chiave di messaggio.
Alan Turing sfrutta l’esperienza di Rejewski
separando il problema della disposizione e
dell’orientamento degli scambiatori, dal
problema dei collegamenti del pannello a prese
multiple. Individua, successivamente, nei crib
(e nelle relative concatenazioni derivanti) la
soluzione al problema. Fa, quindi, costruire le
bombe di Turing (così chiamate perché
discendenti delle bombe di Reiewski).
Muore a Manchester, il 7 Giugno 1954,
mangiando una mela avvelenata con
cianuro di potassio. Si dice che il famoso
simbolo “Apple” dei computer Macintosh
sia un omaggio ad Alan Turing.
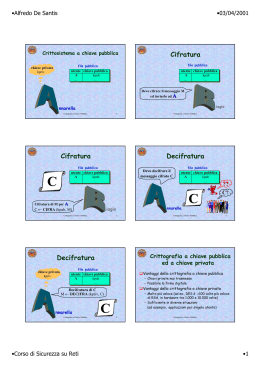
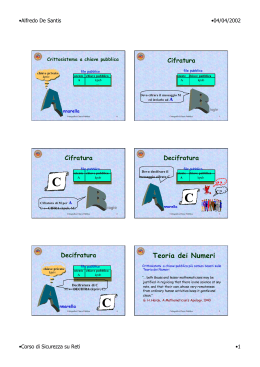
CRITTOGRAFIA ASIMMETRICA
• crittografia MODERNA, A CHIAVE PUBBLICA (1976, Diffie-Hellman)
• doppia chiave per le operazioni di cifratura e decifratura
• la chiave pubblica serve solo per cifrare
• la chiave privata serve solo per decifrare
• è complesso risalire alla chiave privata a partire dalla chiave
pubblica (funzioni unidirezionali)
PREGI:
• non sussiste più il problema della comunicazione della chiave
DIFETTI:
• lentezza
SISTEMA a
“DOPPIA CHIAVE”
Martin Hellman
Withfield Diffie
• la persona A invia il messaggio a B
in una scatola chiusa con lucchetto
tenendosi la chiave
• B riceve la scatola e mette un altro
lucchetto tenendosi a sua volta la
chiave e la rispedisce ad A
• A riceve la scatola, toglie il proprio
lucchetto e la rinvia a B
• B riceve la scatola chiusa e apre il
suo lucchetto con la sua chiave
ALGORITMO RSA
Ron Rivest, Adi Shamir e Leonard Adleman
1977, Massachussets Institute of Technology (MIT), Cambridge
FUNZIONE DI EULERO
associa ad un numero intero n il numero dei numeri interi primi con n e
minori di n (compreso l’uno)
Ф(n)=n(1-1/n1)(1-1/n2).. (1-1/nm)
n1, n2.. nm :fattori primi distinti di n
• se n è primo, allora Ф(n)=n-1
• se n è il prodotto di due numeri primi p e q, allora è facile verificare che
Ф(n)=(p-1)(q-1)
ESEMPIO:
n=18=32*2
Ф(18)=18(1-1/2)(1-1/3)=18(1/2)(2/3)=6
effettivamente, i numeri primi con 18, sono 6 e sono: 1,5,7,11,13,17
ARTIMETICHE FINITE
• si definisce artimetica finita, un’aritmetica che opera su un insieme
limitato di numeri; è detta anche aritmetica modulare o circolare, in quanto
una volta raggiunto l’ultimo numero si ricomincia dal primo (esempi
comunissimi: l’orologio, il contachilometri, i giorni della settimana..)
• in generale un’artimetica finita modulo m si basa sull’insieme {0,1,2..m-1}
i cui numeri possono vedersi anche come i possibili resti di una divisione
per m
• regola di calcolo:
somma e prodotto vengono prima
eseguite nell’aritmetica ordinaria,
non circolare; il risultato viene
diviso per m e si conserva solo il
resto
somma modulo 6
ESEMPIO:
6 + 4 = 2 mod 8
3 + 4 = 1 mod 6
TEOREMA DI FERMAT-EULERO
dati due qualsiasi numeri m ed N primi tra loro, allora
mФ(N) = 1 (mod N)
ESEMPIO:
aritmetica modulo 6
Ф(6)=2
12 = 1
22 = 4
32 = 3
42 = 4
52 = 1
il risultato vale 1 solo per i numeri primi rispetto ad N
• il teorema permette di calcolare l’inverso di un numero in un aritmetica
finita (o modulare)
CALCOLO DELL’INVERSO
NELLE ARITMETICHE FINITE
• l’inverso di un numero a in un aritmetica finita di modulo N è quel numero b per
il quale risulta a*b=1 mod N
• quando a ed N sono numeri primi tra loro, un metodo di calcolo è fornito dal
teorema di Fermat – Eulero
mФ(N) = 1 (mod N)
dove Ф(N) è la funzione di Eulero
• allora l’inverso è semplicemente il numero
b=x Ф(N)-1 mod N
• spesso, per numeri grandi la complessità dell’operazione è proibitiva, pertanto
risulta più efficiente ricorrere all’algoritmo di Euclide per il calcolo dell’MCD
CIFRARIO RSA: IL METODO
(GENERAZIONE DELLE CHIAVI)
• Aldo genera due numeri primi distinti p e q (segreti) e li moltiplica tra loro
ottenendo il numero N (pubblico):
p=5; q=11
N=p*q=55
• Aldo calcola b (segreto) che è la funzione di Eulero di N:
b=Ф(N)=(p-1)(q-1)
b=40
• Aldo calcola il primo numero intero e (pubblico) tale che MCD(e,b)=1:
e=2  MCD(2,40) = 2 NO
e=3  MCD(3,40)=1 SI
e=3
• Aldo calcola il numero d (segreto) inverso di e nell’aritmetica finita di ordine b
che è il più piccolo per cui si ha e*d mod b=1:
d=eb-1 mod N
d=27
CIFRARIO RSA: IL METODO
(CIFRATURA e DECIFRATURA)
• CIFRATURA
• Biagio scompone il messaggio in una sequenza di numeri m (potrebbero
essere, per esempio, i codici ASCII dei singoli caratteri)
• Biagio legge le chiavi pubbliche e ed N di Aldo e trasmette i numeri m uno
alla volta cifrandoli con la formula
c=me mod N
m=7
c=73 mod 55=343 mod 55=13
• DECIFRATURA
• Aldo usa la sua chiave privata d che permette di recuperare m grazie alla
formula
m=cd mod N
m=1327 mod 55=7
LA FIRMA DIGITALE
• Bob cifra il messaggio con la sua chiave privata (operazione di firma) e
successivamente con la chiave pubblica di Alice (operazione di cifratura)
• Alice riceve il messaggio, lo decifra con la sua chiave privata (è, quindi
garantita la confidenzialità) e, da ultimo, decifra il messaggio con la chiave
pubblica di Bob (è, pertanto garantita l’autenticità)
VALORE GIURIDICO
della FIRMA DIGITALE in ITALIA
Decreto Legislativo 4 aprile 2006, n. 159
Articolo 20, comma 1
Il documento informatico da chiunque formato, la registrazione su supporto informatico e la
trasmissione con strumenti telematici conformi […] sono validi e rilevanti agli effetti di legge.
Articolo 21, comma 2
Il documento informatico, sottoscritto con firma digitale o con un altro tipo di firma elettronica
qualificata, ha l’efficacia prevista dall’articolo 2702 del Codice Civile.
Articolo 24, comma 2
L’apposizione di firma digitale integra e sostituisce l’apposizione di sigilli, punzoni, timbri,
contrassegni e marchi di qualsiasi genere ad ogni fine previsto dalla normativa vigente.
Articolo 2702 del Codice Civile
La scrittura privata fa piena prova, fino a querela di falso, della provenienza delle dichiarazioni di
chi l’ha sottoscritta, se […] questa è legalmente considerata come riconosciuta
La validità della firma digitale è garantita dai “certificatori” (disciplinati dagli articoli
26-32) che tengono i registri delle chiavi pubbliche
L’acquisizione di una chiave privata è a pagamento ed ha una scadenza
Bibliografia
[1] Sgarro Andrea, Crittografia, Padova, 1993
[2] P.Ferragina - F.Luccio, Crittografia - Principi, Algoritmi, Applicazioni, Torino,
2001
[3] Singh Simon, Codici e Segreti, Milano, 2002
[4] Stallings William, Crittografia e Sicurezza delle Reti, Milano, 2004
[5] Hodges Andrew, Storia di un Enigma, traduzione di David Mezzacapa, Torino,
1991
Film
[1] Michael Apted, Enigma, 2001
Webografia
[1] http://it.wikipedia.org
[2] http://www.liceofoscarini.it
[3] http://www.zimuel.it/conferenze/iclc2001.pdf
[4] http://www.cs.unibo.it/babaoglu/courses/security/lucidi/critto-1.pdf
Testi
Caterina Urban
Grafica
Caterina Urban
Animazioni
Caterina Urban
..”.. mi piacciono i numeri.. nei numeri verità e bellezza sono un
tutt’uno.. un’equazione può anche darti un sentimento di pura bellezza
e darti la sensazione di essere vicino all’essenza segreta della vita..”..
(Tom Jericho in ENIGMA, film di Michael Apted)