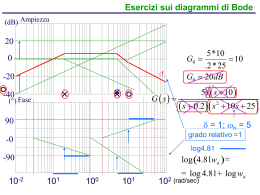
Strumenti per lo studio dei sistemi
continui nel dominio della
frequenza
Strumenti per lo studio dei sistemi continui nel
dominio del tempo e nel dominio della frequenza
Gli argomenti di questa lezione sono:

Le rappresentazioni grafiche
– I diagrammi di Bode
– La rappresentazione nel piano complesso
– Il diagramma polare (o di Nyquist)
Le rappresentazioni grafiche


Non si entra, per ora, nel merito dell’uso delle
rappresentazioni grafiche nello studio dei sistemi
Si cercherà, invece, di stabilire alcune regole di
facile apprendimento per tracciare, nel più
immediato dei modi ed almeno in prima
approssimazione, due tipiche rappresentazioni
grafiche per le funzioni di trasferimento:
– i diagammi di Bode
– il diagramma polare (o di Nyquist)
I diagrammi di Bode
Le rappresentazioni grafiche
I diagrammi di Bode




I diagrammi di Bode sono due diagrammi
semilogaritmici
Nel primo diagramma di Bode si rappresenta il
valore, in dB, del modulo (o ampiezza) di una
funzione G(s) al variare di w, posto s=jw
Nel secondo diagramma di Bode si rappresenta la
fase della funzione G(s)
Si ricorda che la funzione G(s) è una funzione
complessa con parte reale Re[G(s)] e coefficiente
della parte immaginaria Im[G(s)]



Le rappresentazioni grafiche
I diagrammi di Bode
Cosa si intende per diagrammi semilogaritmici?
Sono diagrammi con assi ortogonali, come quelli
cartesiani, nei quali, però, l’asse delle ascisse è
graduato secondo il logaritmo (in base 10) della
variabile indipendente (che qui è w)
Ricordando che
Precisazione: si noti che la funzione logaritmo
log100 = -
non è, in effetti, definita per l’argomento 0;
log101 = 0
-, dunque, è in realtà il limite di tale
log1010 = 1
funzione quando l’argomento tende a 0
log10100 = 2
e così via, si ha il diagramma che segue
Le rappresentazioni grafiche
I diagrammi di Bode
L’intervallo La
fra variabile
una “tacca”
e l’altra,
sull’asse
delle
cioè ogni volta
che èlog
aumenta w
ascisse
la w
pulsazione
di 1, si dice decade
0
1
2
3
10
10
10
101
100
102
1.000
103
4
5
10.000
104 100.000
105
log
w [rad/s]
decade decade decade decade decade

w
Poiché, come si è detto nella slide precedente, il logaritmo di 0 tende a - ,
naturalmente lo 0 in questo diagramma non può essere rappresentato!
Le rappresentazioni grafiche
I diagrammi di Bode : diagramma del modulo
 È noto che il modulo di G(s) può essere calcolato
come:
|G(s)| =

Re[G(s)]2+Im[G(s)]2
Il suo valore in dB è, naturalmente:
|G(s)|dB = 20 log |G(s)|

Si noti che
– se |G(s)|=1  |G(s)|dB=0
– se |G(s)|>1  |G(s)|dB>0
– se |G(s)|<1  |G(s)|dB<0
Le rappresentazioni grafiche
I diagrammi di Bode: diagramma del modulo
|G(s)|dB
80
60
40
20
-20
-40
-60
-80
La variabile sull’asse delle ordinate è il
modulo, espresso in dB, |G(s)|dB
100
101
102
103
104
105
w
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode : diagramma della fase

La fase di G(s) può essere calcolata come:
j = tan-1
Im[G(s)]
Re[G(s)]

La fase può essere espressa in gradi o in radianti

Si ricordi che
0° = 0 [rad]
90° = p/2 [rad]
180° = p [rad]
Le rappresentazioni grafiche
I diagrammi di Bode: diagramma della fase
[°]
j [rad]
180°
p
135°
3p/4
90°
p/2
45°
p/4
-45
-p/4
-90
-p/2
-135°
-3p/4
-180
-p
La variabile sull’asse delle
ordinate è la fase j
100
101
102
103
104
105
w
[rad/s]


Le rappresentazioni grafiche
I diagrammi di Bode
Per imparare le regole per la costruzione di un
diagramma di Bode si partirà dall’illustrazione di
alcuni esempi classici dai quali dedurre le regole
fondamentali
Illustreremo di seguito la rappresentazione delle
seguenti funzioni:
–
–
–
–
–
–
G(s)
G(s)
G(s)
G(s)
G(s)
G(s)
=
=
=
=
=
=
k
(k=costante reale positiva)
s
k•s
1/s
1+t•s
1/(1+t•s)
La funzione G(s)=k
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=k

Posto s=jw, possiamo senz’altro dire che il valore in
dB del modulo della funzione G(jw) è
|G(jw)|dB = 20•log|k|

Tale valore è
– 0 se k=1
– positivo se k>1
– negativo se k<1

La G(s) ha in questo caso parte reale Re[G(s)]=k e
coefficiente della parte immaginaria nulla per cui
j = tan-1 0 = 0
Le rappresentazioni grafiche
La funzione G(s)=k: diagramma del modulo
|G(jw)|dB
80
60
40
20
-20
-40
-60
-80
k=1  |G(jw)|dB = 0
per ogni valore di w
k<1  |G(jw)|dB < 0
per ogni valore di w
100
101
102
103
104
k>1  |G(jw)|dB > 0
per ogni valore di w
105
w
[rad/s]
Le rappresentazioni grafiche
La funzione G(s)=k: diagramma della fase
j [rad]
p
3p/4
p/2
p/4
-p/4
-p/2
-3p/4
-p
100
101
j = 0° per ogni valore di w
102
103
104
105
w
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=k
Riepilogando


La funzione G(s)=k (costante reale positiva) ha un
modulo in dB costante e pari a 20•logk
Tale funzione non introduce alcuno sfasamento,
cioè la sua fase è costantemente nulla al variare
della pulsazione w
La funzione G(s)=s
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=s

Posto s=jw, si calcola facilmente che il valore in dB
del modulo della funzione G(jw) è
|G(jw)|dB = 20 logw

Tale valore è
– 0 quando w=1
– cresce linearmente di 20 dB ogni volta che log w
aumenta di 1, cioè per ogni decade

La G(s) ha in questo caso parte reale nulla e coefficiente della parte immaginaria Im[G(s)]=w per cui
j = arctg (w/0) = 90° = p/2
Le rappresentazioni grafiche
La funzione G(s)=s: diagramma del modulo
|G(jw)|dB
80
60
40
20
-20
-40
-60
-80
ed aumenta di 20 dB
100
101
102
103
104
105
per ogni decade
|G(jw)|dB vale 0
quando w = 1
w
[rad/s]
Le rappresentazioni grafiche
La funzione G(s)=s: diagramma della fase
j [rad]
j = 90° per ogni valore di w
p
3p/4
p/2
p/4
-p/4
-p/2
-3p/4
-p
100
101
102
103
104
105
w
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=s
Riepilogando



La funzione G(s)=s ha uno zero nell’origine (cioè
per s=0 si ha G(s)=0)
Tale funzione G(s)=s ha un modulo in dB che si
annulla per w=1 e che cresce di 20 dB per decade
Inoltre essa introduce uno sfasamento, costante al
variare di w, di 90°
La funzione G(s)=k•s



Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=k•s
Posto s=jw, il valore in dB del modulo della
funzione G(jw), per le proprietà dei logaritmi, si
calcola facendo la somma dei logaritmi di k ed w
|G(jw)|dB = 20•log(|k|•w) = 20•log|k| + 20•logw
Come si vede, è la somma delle funzioni viste in
precedenza; il grafico del modulo risulta quindi
uguale al grafico della funzione G(s)=s traslato
verticalmente del valore di 20•log|k|
Il diagramma della fase è identico a quello della
G(s)=s in quanto la parte reale di G(s)=k•s è nulla
j = arctg (kw/0) = 90° = p/2
Le rappresentazioni grafiche
La funzione G(s)=k•s: diagramma del modulo
|G(jw)|dB
80
60
40
20
-20
-40
-60
-80
= diagramma di G(s)=k•s
Diagramma di G(s)=s
100
101
102
103
104
+ diagramma di G(s)=k
105
w
[rad/s]
Le rappresentazioni grafiche
La funzione G(s)=k•s: diagramma della fase
j [rad]
j = 90° per ogni valore di w
p
3p/4
p/2
p/4
-p/4
-p/2
-3p/4
-p
100
101
102
103
104
105
w
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=k•s

Da quanto visto sulle rappresentazioni di tale
funzione è possibile ricavare una regola generale
Il prodotto di una costante k (reale e
positiva) su una funzione G(s) incide sui
diagrammi di Bode nel seguente modo:
 Il diagramma del modulo risulta traslato
verticalmente del valore 20•log|k|
 Il diagramma della fase rimane invariato

Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=k•s




Annotazione:
la regola enunciata corrisponde al fatto che il
modulo del prodotto di due numeri complessi è pari
al prodotto dei moduli, mentre la fase di tale
prodotto è pari alla somma delle fasi
Il numero reale k ha modulo |k| ed ha fase nulla
Quindi, nel modulo in dB, per la proprietà dei
logaritmi, il valore 20•log|k| si somma a 20•logw
Inoltre, visto che k ha fase nulla, la fase di
G(s)=k•s è uguale a quella di s, cioè sempre 90°
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=k•s


Sul diagramma del modulo si deve fare un’altra
fondamentale considerazione
Il modulo in dB, assume valore 0 quando
|G(s)|dB=20•(log|k|+logw)=0
e quindi, con qualche passaggio algebrico, quando
logw=-log|k|  logw=log|k|-1  w=|k|-1  w=1/|k|

Il numero reale 1/|k| è dunque l’intersezione con
l’asse delle ascisse della curva del modulo in dB
della funzione G(s)=k•s
Le rappresentazioni grafiche
La funzione G(s)=k•s: diagramma del modulo
|G(jw)|dB
80
60
40
20
-20
-40
-60
-80
Diagramma di G(s)=k•s
1/|k|
100
101
102
103
104
Intersezione = 1/|k|
105
w
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=k•s
Riepilogando




La funzione G(s)=k•s ha uno zero nell’origine (cioè
per s=0 si ha G(s)=0)
Tale funzione ha un modulo in dB che si annulla
per w=1/|k| e che cresce di 20 dB per decade
Il suo modulo in dB può comunque essere sempre
calcolato come somma del modulo in dB della
funzione k e del modulo in dB della funzione s
Inoltre la funzione G(s)=k•s introduce uno
sfasamento, costante al variare di w, di 90°
La funzione G(s)=1/s
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1/s



Posto s=jw, il valore in dB del modulo della funzione
G(jw), per le proprietà dei logaritmi, si calcola mediante
la differenza
|G(jw)|dB=20•log(1/w)=20•(log1-logw)=-20•logw
Poiché la funzione G(s)=1/s ha un modulo in dB che è
pari a quello della funzione G(s)=s col segno cambiato,
il suo diagramma del modulo risulta ribaltato
verticalmente rispetto a quello di G(s)=s
Quanto alla fase, ricordando che la divisione di due
numeri complessi ha fase pari alla differenza delle fasi,
essa sarà
j = j(1)-j(s) = 0°-90° = -90° = -p/2
Le rappresentazioni grafiche
La funzione G(s)=1/s: diagramma del modulo
|G(jw)|dB
80
60
40
20
-20
-40
-60
-80
Diagramma di G(s)=1/s
100
101
102
Diagramma di G(s)=s
w [rad/s]
103
104
105
Le rappresentazioni grafiche
La funzione G(s)=1/s: diagramma della fase
j [rad]
p
3p/4
p/2
p/4
-p/4
-p/2
-3p/4
-p
j = -90° per ogni valore di w
100
101
102
103
104
105
w
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1/s
Esercizio
Tracciare i diagrammi di Bode della
funzione G(s)=k/s
Suggerimento: si noti che tale funzione è il
prodotto di k e di 1/s
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1/s
Riepilogando




La funzione G(s)=1/s ha un polo nell’origine (cioè
per s=0, G(s) ha una singolarità)
Tale funzione ha un modulo in dB che si annulla
per w=1 e che decresce di 20 dB per decade
Il suo modulo in dB può comunque essere calcolato
sempre come differenza del modulo in dB della
funzione 1 (che è pari a 0) e del modulo in dB della
funzione s
Inoltre la funzione G(s)=1/s introduce uno
sfasamento, costante al variare di w, di -90°
La funzione G(s)=1+ts
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1+ts
 Posto s=jw, il modulo di G(s) è dato da
|G(jw)| =

12+(tw)2
Tale valore è
– praticamente pari ad 1 quando tw << 1
– praticamente pari a tw quando tw>>1

Il diagramma del modulo, quindi, assume
– l’andamento della funzione G(s)=1 per valori di w
prossimi a 0
– l’andamento della funzione G(s)=ts per valori di w
molto grandi

Questi andamenti sono asintotici per G(s)=1+ts
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1+ts
 Inoltre, come si è già visto, il diagramma del
modulo della funzione G(s)=ts interseca l’asse
delle ascisse nel punto w=1/|t|
 Ma si può notare anche che il valore s=-1/t annulla
la funzione G(s); esso è quindi uno zero della
funzione G(s)
 Si può allora trarre la conclusione che l’asintoto di
G(s)=1+ts, quando w è molto grande, è proprio la
retta che passa per il punto w=1/|t|, valore che è
proprio il valore assoluto dello zero di G(s), e
cresce di 20 dB per decade
Le rappresentazioni grafiche
La funzione G(s)=1+ts: diagramma del modulo
80
60
40
20
-20
-40
-60
-80
Diagrammaasintotico
di G(s)=ts
|G(jw)|dB Diagramma
asintoto per
w molto grande
risultante
di G(s)=1+ts
1/|t|
100
101
102
103
104
Diagramma di G(s)=1
asintoto per w molto piccolo
105
w
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1+ts


Annotazione:
più volte è stata usata l’espressione
diagramma asintotico;
tale espressione significa che il diagramma
costruito è solo un’approssimazione
dell’andamento effettivo della funzione
G(s)=1+ts
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1+ts
Esercizio
 Calcolare
lo scostamento del
diagramma reale della funzione
G(s)=1+t•s rispetto al diagramma
asintotico nel punto w=1/|t|
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1+ts
Soluzione




Per w=1/|t|, G(jw)=1+jt•w=1±j
In tal caso, il modulo di G(jw)=1±j è pari alla
radice di 2 cioè
|G(jw)|=1,4142
Il valore in dB è dunque
|G(jw)|dB= 20•log1,4142 = 3 dB
Poiché nel punto w=1/|t| il modulo rappresentato
nel diagramma asintotico assume il valore 0 dB, lo
scostamento richiesto è proprio pari a 3 dB
Le rappresentazioni grafiche
La funzione G(s)=1+ts: soluzione esercizio
Diagramma asintotico
|G(jw)|dB
G(s)=1+ts
80
60
40
20
-20
-40
-60
-80
Andamento
effettivo di G(s)
100
101
1/|t|
102
3 dB
103
104
105
w
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1+ts


Per quanto riguarda la fase, si nota che quando w è
molto piccolo, il rapporto Im[G(s)]/Re[G(s)] diventa
praticamente nullo
La fase, per w molto piccolo, è quindi
j = arctg {Im[G(s)]/Re[G(s)]}  0

Per un valore molto grande di w, viceversa, il
rapporto Im[G(s)]/Re[G(s)] diventa praticamente
+ e quindi
j = arctg {Im[G(s)]/Re[G(s)]}  90° = p/2
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1+ts



I diagrammi di fase visti per G(s)=1 e per G(s)=ts
sono quindi gli asintoti del diagramma della fase
della funzione G(s)=1+ts, rispettivamente per w
molto piccolo e per w molto grande
Si può notare inoltre che quando w=1/|t|, come si
è visto dal precedente esercizio, G(s)=1+j e quindi
la fase risulta j = arctg 1 = 45° = p/4
Il diagramma della fase della funzione G(s)=1+ts
passa quindi per il punto individuato dalle
coordinate w=1/t e j=p/4
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1+ts

Per completare il diagramma asintotico della fase,
senza aggiungere ulteriori spiegazioni, che sono un
po’ più complesse, si deve chiarire che il passaggio
da un asintoto all’altro avviene quasi totalmente
nell’arco di due decadi, la decade a sinistra dello
zero e la decade a destra dello zero
Le rappresentazioni grafiche
Il diagramma passa
La funzione G(s)=1+ts: diagramma della fase
per questo punto
j [rad]
p
3p/4
p/2
p/4
-p/4
-p/2
-3p/4
decade
dopo
Asintoto per w
molto grande
1/|t|
100
101
102
decade
prima
-p
Asintoto
per w
molto piccolo
103
104
105
w
Diagramma
asintotico
della
Asintoto
obliquo
fase completo
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1+ts
Riepilogando



La funzione G(s)=1+ts ha uno zero per s=-1/t
Tale funzione ha un modulo in dB sempre
crescente con w
Si può tracciare un diagramma asintotico del
modulo che è:
– pari a 0 per w<1/|t|
– aumenta di 20 dB per decade per w>1/|t|
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1+ts
Riepilogando


Inoltre la funzione G(s)=1+ts introduce uno
sfasamento cresente al variare di w
Si può tracciare un diagramma asintotico della fase
che è:
– pari a 0° per w<1/|t| - una decade
– aumenta di 45° per ciascuna delle due decadi
successive (w compreso fra 1/|t| - una decade e
1/|t| + una decade)
– pari a 90° per w>1/|t| + una decade
La funzione G(s)=1/(1+ts)
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1/(1+ts)




Questa funzione si comporta nei confronti della
funzione G(s)=1+ts come la funzione G(s)=1/s si
comportava nei confronti della funzione G(s)=s
Il diagramma asintotico del modulo è quindi come
quello della funzione G(s)=1+ts ribaltato in senso
verticale
Il valore s=-1/t annulla il denominatore della
funzione G(s) ed è quindi un polo (non uno zero)
Anche in questo caso, il punto w=1/|t| è
l’intersezione fra l’asse delle ascisse e l’asintoto per
w molto grande
Le rappresentazioni grafiche
La funzione G(s)=1/(1+ts): diagramma del
modulo
|G(jw)|dB
80
60
40
20
-20
-40
-60
-80
Diagramma asintotico
di G(s)=1/(1+ts)
1/t
100
101
102
103
104
105
Diagramma asintotico
di G(s)=1+ts
w
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1/(1+ts)


Per quanto riguarda la fase, notiamo che per la
proprietà già ricordata sulla fase del quoziente di
due numeri complessi, la fase di G(s) è pari alla
fase di 1, che vale 0, meno la fase di (1+ts), di cui
è già noto il diagramma asintotico di fase
Il diagramma asintotico di fase di G(s) risulta quindi
dal ribaltamento in verticale del diagramma
asintotico di fase visto prima per la funzione
(1+ts)
Le rappresentazioni grafiche
La funzione G(s)=1/(1+ts): diagramma della
fase
j [rad]
p
3p/4
p/2
p/4
-p/4
-p/2
-3p/4
-p
Diagramma asintotico
di fase di G(s)
1/t
100
101
102
103
104
105
Diagramma asintotico
di fase di (1+ts)
w
[rad/s]
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1/(1+ts)
Esercizio
 Tracciare
i diagrammi di Bode della
funzione G(s)=k/(1+ts)
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)=1/(1+ts)
Riepilogando



La funzione G(s)=1/(1+ts) ha un polo per s=-1/t
Tale funzione ha un modulo in dB sempre
decrescente con w
Si può tracciare un diagramma asintotico del
modulo che è:
– pari a 0 per w<1/|t|
– diminuisce di 20 dB per decade per w>1/|t|
Le rappresentazioni grafiche
I diagrammi di Bode: la funzione G(s)= 1/(1+ts)
Riepilogando


Inoltre la funzione G(s)=1/(1+ts) introduce uno
sfasamento decresente al variare di w
Si può tracciare un diagramma asintotico della fase
che è:
– pari a 0° per w<1/|t| - una decade
– diminuisce di 45° per ciascuna delle due decadi
successive (w compreso fra 1/|t| - una decade e
1/|t| + una decade)
– pari a -90° per w>1/|t| + una decade
Il prodotto di funzioni




Le rappresentazioni grafiche
I diagrammi di Bode: il prodotto di funzioni
Si consideri il caso di una funzione di trasferimento
F(s) che sia genericamente il prodotto di due o più
funzioni come quelle degli esempi visti
Per semplicità si fissi F(s)=A(s)•B(s) con A(s)=1+t1s
e B(s)= 1+t2s e t1>t2
I valori s=-1/t1 ed s=-1/t2 annullano la F(s) e sono
quindi zeri di F(s)
Per le solite proprietà dei logaritmi, il modulo in dB,
di F(s), posto s=jw, è
|F(s)|dB = 20•log(|1+jwt1|•|1+jwt2|) =
=20•log|1+jwt1|+20•log|1+jwt2|=|A(s)|dB+|B(s)|dB
Le rappresentazioni grafiche
I diagrammi di Bode: il prodotto di funzioni



Si conoscono già gli andamenti dei diagrammi
asintotici del modulo di A(s) e B(s), per cui basta
fare una somma grafica dei due diagrammi
Nel fare questa somma si vede che i tratti in
pendenza danno luogo ad un assommarsi delle
pendenze
Succede allora che il diagramma asintotico del
modulo di F(s) è
– nullo per w<1/|t1|
– ha una pendenza di +20 dB per decade fino a 1/|t2|
– ha una pendenza di +40 dB per decade per w>1/|t2|
Le rappresentazioni grafiche
Il prodotto di funzioni: diagramma del modulo
Diagramma asintotico
|F(jw)|dB
di A(s)=(1+t1s)
80 Diagramma asintotico
60
di F(s)=A(s)•B(s)
Pendenza 40 dB
40
per decade
20
1/t1
1/t2
-20
-40
-60
-80
100
101
102
|F(s)|dB=0
103
104
105
w
[rad/s]
Pendenza 20 dB
Diagramma asintotico
per decade
di B(s)=1+t2s
Le rappresentazioni grafiche
I diagrammi di Bode: il prodotto di funzioni
Per quanto riguarda la fase, si ricordi che la
fase di un prodotto complesso è uguale alla
somma delle fasi dei fattori; quindi, anche in
questo caso, si può fare una somma grafica
dei diagrammi asintotici della fase di A(s) e
di B(s)
 Valgono le considerazioni già dette sui tratti
in pendenza

Le rappresentazioni grafiche
I diagrammi di Bode: il prodotto di funzioni
Esercizio
 Tracciare
il diagramma di Bode della
fase della funzione
F(s) = A(s)•B(s) = (1+t1s)•(1+t2s)
Le rappresentazioni grafiche
I diagrammi di Bode: il prodotto di funzioni
Riepilogando


Nel fare un prodotto di due funzioni il diagramma
asintotico del modulo si può ricavare facendo una
somma grafica dei diagrammi asintotici dei moduli
delle singole funzioni
Anche il diagramma asintotico della fase può
ottenersi come somma grafica dei diagrammi
asintotici delle fasi delle singole funzioni
Il rapporto di funzioni





Le rappresentazioni grafiche
I diagrammi di Bode: il rapporto di funzioni
Si consideri, infine, il caso di una F(s) che sia il
rapporto di due funzioni come quelle viste finora
Per semplicità si fissi F(s)=A(s)/B(s) con
A(s)=1+t1s e B(s)= 1+t2s e t1>t2
s=-1/t1 annulla la A(s) ed è quindi uno zero di F(s)
s=-1/t2 annulla la B(s) ed è quindi un polo di F(s)
Per le solite proprietà dei logaritmi, il modulo in dB,
di F(s), posto s=jw, è
|F(s)|dB = 20•log(|1+jwt1|/|1+jwt2|) =
=20•log|1+jwt1|-20•log|1+jwt2|=|A(s)|dB-|B(s)|dB
Le rappresentazioni grafiche
I diagrammi di Bode: il rapporto di funzioni



Si conoscono già gli andamenti dei diagrammi
asintotici del modulo di A(s) e B(s), per cui basta
fare una differenza grafica dei due diagrammi
Nel fare questa differenza si vede che i tratti in
pendenza danno luogo ad una compensazione
delle pendenze
Succede allora che il diagramma asintotico del
modulo di F(s) è
– nullo per w<1/|t1|
– ha una pendenza di 20 dB per decade fino a 1/|t2|
– ha una pendenza nulla per w>1/|t2|
Le rappresentazioni grafiche
Il rapporto di funzioni: diagramma del modulo
Diagramma asintotico
|F(jw)|dB
di A(s)=(1+t1s) Pendenza di
80 Diagramma asintotico
nuovo nulla
60
di F(s)=A(s)/B(s)
40
20
-20
-40
-60
-80
1/t1
100
101
1/t2
102
|F(s)|dB=0
103
104
105
w
[rad/s]
Pendenza 20 dB
Diagramma asintotico
per decade
di B(s)=1+t2s
Le rappresentazioni grafiche
I diagrammi di Bode: il rapporto di funzioni
Esercizio
 Cosa
succederebbe nel diagramma
di Bode appena visto nel caso
in cui t2>t1 ?
Le rappresentazioni grafiche
I diagrammi di Bode: il rapporto di funzioni


Per quanto riguarda la fase, si ricordi che la fase di
un rapporto complesso è uguale alla differenza
delle fasi del numeratore e del denominatore;
quindi, anche in questo caso, si può fare una
differenza grafica dei diagrammi asintotici della fase
di A(s) e di B(s)
Valgono le considerazioni già dette sui tratti in
pendenza
Le rappresentazioni grafiche
I diagrammi di Bode: il rapporto di funzioni
Esercizio
 Tracciare
il diagramma di Bode della
fase della funzione
F(s) = A(s)/B(s) = (1+t1s)/(1+t2s)
nel caso t1>t2 e nel caso opposto t2>t1
Le rappresentazioni grafiche
I diagrammi di Bode: il rapporto di funzioni
Riepilogando


Nel fare un rapporto di due funzioni il diagramma
asintotico del modulo si può ricavare facendo una
differenza grafica dei diagrammi asintotici dei
moduli delle singole funzioni
Anche il diagramma asintotico della fase può
ottenersi come differenza grafica dei diagrammi
asintotici delle fasi delle singole funzioni
Le rappresentazioni grafiche
I diagrammi di Bode: conclusioni

Concludendo è possibile fare le seguenti
considerazioni:
– grazie alle proprietà dei logaritmi nei diagrammi di
Bode del modulo si può operare con somme e
differenze grafiche;
– da ciò consegue che ogni volta che si raggiunge uno
zero la pendenza del diagramma asintotico aumenta
di 20 dB per decade
– ed ogni volta che si raggiunge un polo la pendenza
decresce di 20 dB per decade
Le rappresentazioni grafiche
I diagrammi di Bode: conclusioni




Il valore iniziale del modulo in dB è il cosiddetto
guadagno statico della G(s) e si può calcolare
imponendo w=0
La rappresentazione del guadagno statico nel
diagramma di Bode del modulo è impossibile in
quanto se w=0, logw non è definito ( -)
Tale valore è però utilissimo in quanto ci permette
di individuare l’andamento asintotico del modulo
per w tendente a 0
Le stesse considerazioni valgono per w  +
Le rappresentazioni grafiche
I diagrammi di Bode: conclusioni

Considerazioni del tutto simili a quelle fatte per il
diagramma di Bode del modulo, possono essere
fatte per il diagramma di Bode della fase grazie al
fatto che in un prodotto di numeri complessi le fasi
si sommano mentre in un rapporto di numeri
complessi si fa la differenza delle fasi del
numeratore e del denominatore