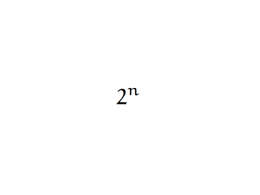ITERAZIONE e RICORSIONE
(eseguire uno stesso calcolo ripetutamente)
ITERAZIONE: ripetere piu’ volte una sequenza di operazioni
istruzioni: for, while, do while.
Es. somma i primi n interi: ( ( ( (1)+ 2) +3)+…+ n)
for (i=1, i<=n, i++) somma=somma +i
ITERAZIONE e RICORSIONE
(eseguire uno stesso calcolo ripetutamente)
ITERAZIONE: ripetere piu’ volte una sequenza di operazioni
istruzioni: for, while, do while.
Es. somma i primi n interi: ( ( ( (1)+ 2) +3)+…+ n)
for (i=1, i<=n, i++) somma=somma +i
Es. Cerca il minimo tra A[0],…,A[n-1]
{min=A[0];
for (i=1, i<n, i++) if (A[i]<min) min=A[i]}
SORTING (Ordinamento)
Ordinare una lista significa permutare gli elementi in
modo da averli in ordine non decrescente da sinistra a
destra
lista iniziale
(3,1,4,1,5,9,2,6,3)
SORTING (Ordinamento)
Ordinare una lista significa permutare gli elementi in
modo da averli in ordine non decrescente da sinistra a
destra
lista iniziale
(3,1,4,1,5,9,2,6,3)
lista ordinata (1,1,2,3,3,4,5,6,9)
La lista ordinata contiene gli stessi elementi e conserva
il numero di occorrenze di ogni valore
LISTA ORDINATA
Date le variabili a e b, ab
se e solo se il valore di a è minore di quello di b
oppure a e b hanno lo stesso valore
Una lista (a0,a1,…,an-1) è ordinata (sorted) se a0 a1 …  an-1
LISTA ORDINATA
Date le variabili a e b, ab
sse il valore di a è minore di quello di b
oppure a e b hanno lo stesso valore
Una lista (a0,a1,…,an-1) è ordinata (sorted) se a0 a1 …  an-1
SORTING (Ordinamento)
Input: lista (a0,a1,…,an-1)
output: lista (b0,b1,…,bn-1) tale che
1. è una lista ordinata
2. è una permutazione della lista input, ogni
elemento appare con la stessa molteplicità
nelle due liste
SELECTION SORT (algoritmo iterativo)
La lista da ordinare è contenuta in un array A di n interi.
METODO.
Iteriamo il seguente passo: l’array A è diviso in 2 parti
Parte iniziale ordinata | parte da ordinare
cerchiamo l’elemento minimo nella parte non ordinata
e lo scambiamo con il primo della parte non ordinata
SELECTION SORT (algoritmo iterativo)
La lista da ordinare è contenuta in un array A di n interi.
METODO. Iteriamo il passo: l’array A è diviso in 2 parti
Parte iniziale ordinata | parte da ordinare
cerchiamo l’elemento minimo nella parte non ordinata
e lo scambiamo con il primo della parte non ordinata
I iterazione: A[0..n-1] non ordinato, cerca minimo di
A[0..n-1] e scambialo con A[0]. Quindi: A[0] |A[1..n-1]
SELECTION SORT (algoritmo iterativo)
La lista da ordinare è contenuta in un array A di n interi.
METODO. Iteriamo il passo: l’array A è diviso in 2 parti
Parte iniziale ordinata | parte da ordinare
cerchiamo l’elemento minimo nella parte non ordinata
e lo scambiamo con il primo della parte non ordinata
I iterazione: A[0..n-1] non ordinato, cerca minimo di
A[0..n-1] e scambialo con A[0]. Quindi: A[0] |A[1..n-1]
II iterazione: A[0] ordinato, A[1..n-1] non ordinato,
cerca minimo di A[1..n-1] e scambialo con A[1]. Quindi:
A[0]A[1] A[2..n-1]
SELECTION SORT (algoritmo iterativo)
Parte iniziale ordinata | parte da ordinare
I iterazione: A[0..n-1] non ordinato, cerca minimo di
A[0..n-1] e scambialo con A[0]. Quindi: A[0] |A[1..n-1]
II iterazione: A[0] ordinato, A[1..n-1] non ordinato,
cerca minimo di A[1..n-1] e scambialo con A[1]. Quindi:
A[0]A[1] A[2..n-1]
generica iterazione:
A[0..i-1] ordinato, A[i..n-1] non ordinato,
cerca minimo di A[i..n-1] e scambialo con A[i].
Quindi: A[0..i] A[i+1..n-1]
SELECTION SORT (algoritmo iterativo)
Parte iniziale ordinata | parte finale da ordinare
I iterazione: A[0..n-1] non ordinato, cerca minimo di
A[0..n-1] e scambialo con A[0]. Quindi: A[0] |A[1..n-1]
II iterazione: A[0] ordinato, A[1..n-1] non ordinato,
cerca minimo di A[1..n-1] e scambialo con A[1]. Quindi:
A[0]A[1] A[2..n-1]
generica iterazione:
A[0..i-1] ordinato, A[i..n-1] non ordinato,
cerca minimo di A[i..n-1] e scambialo con A[i].
Quindi: A[0..i] A[i+1..n-1]
Per i=n-2: A[0..n-2] A[n-1]. ARRAY ORDINATO
SELECTION SORT (algoritmo iterativo)
(1) for (i=0,i<n-1,i++)
{
(2)
small=i /* variabile small rappresenta la prima occorrenza
del minimo di A[i..n-1]*/
(3)
for (j=i+1, j<n,j++) if (A[j]<A[small]) small=j;
/* trova indice del minimo e mettilo in small */
(4)
temp=A[small];
(5)
A[small]=A[i];
(6)
A[i]=temp; /* scambia valori di A[i] ed A[small]*/
}
SELECTION SORT (algoritmo iterativo)
(1) for (i=0,i<n-1,i++)
{
(2)
small=i /* variabile small rappresenta la prima occorrenza
del minimo di A[i..n-1]*/
(3)
for (j=i+1, j<n,j++) if (A[j]<A[small]) small=j;
/* trova indice del minimo e mettilo in small */
(4)
temp=A[small];
(5)
A[small]=A[i];
(6)
A[i]=temp; /* scambia valori di A[i] ed A[small]*/
}
Es. A=[5|7]
i=0, small=0
j=1, A[1]>A[small]
Scambia A[0] e A[0]
Risultato A[5|7]
SELECTION SORT (algoritmo iterativo)
(1) for (i=0,i<n-1,i++)
{
(2)
small=i /* variabile small rappresenta la prima occorrenza
del minimo di A[i..n-1]*/
(3)
for (j=i+1, j<n,j++) if (A[j]<A[small]) small=j;
/* trova indice del minimo e mettilo in small */
(4)
temp=A[small];
(5)
A[small]=A[i];
(6)
A[i]=temp; /* scambia valori di A[i] ed A[small]*/
}
Es. A=[5|7]
i=0, small=0
j=1, A[1]>A[small]
Scambia A[0] e A[0]
Risultato A[5|7]
Es. A=[7|5]
i=0, small=0
j=1, A[1]<A[small], small=1
Scambia A[0] e A[1]
Risultato A[5|7]
Es. A=[40|30|20|10]
i=0, small=0
j=1, A[1]=30<A[small]=40, small=1
j=2, A[2]=20<A[small]=A[1]=30, small=2
j=3, A[3]=10<A[small]=A[2]=20, small=3
Scambia A[0] e A[3]
Risultato Parziale A=[10|30|20|40]
Es. A=[40|30|20|10]
i=0, small=0
j=1, A[1]=30<A[small]=40, small=1
j=2, A[2]=20<A[small]=A[1]=30, small=2
j=3, A[3]=10<A[small]=A[2]=20, small=3
Scambia A[0] e A[3]
Risultato Parziale A=[10|30|20|40]
i=1, small=1
j=2, A[2]=20<A[small]=A[1]=30, small=2
j=3, A[3]=40>A[small]=A[2]=20
Scambia A[1] e A[2]
Risultato Parziale A=[10|20|30|40]
Es. A=[40|30|20|10]
i=0, small=0
j=1, A[1]=30<A[small]=40, small=1
j=2, A[2]=20<A[small]=A[1]=30, small=2
j=3, A[3]=10<A[small]=A[2]=20, small=3
Scambia A[0] e A[3]
Risultato Parziale A=[10|30|20|40]
i=1, small=1
j=2, A[2]=20<A[small]=A[1]=30, small=2
j=3, A[3]=40>A[small]=A[2]=20
Scambia A[1] e A[2]
Risultato Parziale A=[10|20|30|40]
i=2, small=2
j=3, A[3]=40>A[small]=A[2]=30
Scambia A[2] e A[2]
Risultato A=[10|20|30|40] =[10|20|30|40] ordinato
Esercizi. Simulare l’esecuzione del selection sort per i
seguenti array:
• A=[6|8|14|17|23]
• A=[17|23|14|6|8]
• A=[23|17|14|6|6]
ORDINE LESSICOGRAFICO
Possiamo ordinare ogni volta che esiste una relazione
di “minore” ( < ).
Ordina lessicografico: Dato un alfabeto A con un ordine
sulle lettere (es. a<b<c<…<z) ed una coppia di sequenze
c1c2 …ck, d1d2…dm risulta
c1c2 …ck < d1d2…dm
1) se k<m e c1=d1,…,ck=dk
2) oppure c1=d1,..,ci-1=di-1, ci<di per qualche i.
Es. 1)
ala < alato
Es. 2)
alano < alati
(n < t)
albero < foglia (a<f)
SORTING ON KEYS
A volte vogliamo ordinare usando solo una parte specifica
dei valori (KEY).
Se abbiamo delle strutture possiamo ordinare su di un
solo campo
Es. type struct studente {
int matricola;
chararray nome
int voto}
possiamo ordinare secondo uno dei 3 campi.
Se ordiniamo per matricola allora dobbiamo confrontare i
campi matricola.Nel SelectionSort, A è un array di
strutture e si hanno i confronti
A[j].matricola < A[small].matricola
INDUZIONE
Data una affermazione S(n), vogliamo dimostrare che
essa vale per ogni intero n>a.
Es.
S(n): risulta
n(n  1)
i  (1  2  ...  n) 

2
i 1
n
Si vuole dimostrare che S(n) vale per ogni n > 1.
INDUZIONE
Vogliamo dimostrare che S(n) vale per ogni intero n>a.
INDUZIONE
Vogliamo dimostrare che S(n) vale per ogni intero n>a.
Una dimostrazione per induzione consiste di 2 fasi
1. BASE INDUTTIVA. Si dimostra che l’affermazione è
vera per il primo valore, cioè S(a) è vera.
2. PASSO INDUTTIVO. Assumiamo che S(n-1) è vera e
dimostriamo che allora anche S(n) è vera.
INDUZIONE
1. BASE INDUTTIVA. S(a) è vera.
2. PASSO INDUTTIVO. S(n-1) implica S(n) vera.
Es.
S(n):
n(n  1)
i  (1  2  ...  n) 

2
i 1
n
Si vuole dimostrare che S(n) vale per ogni n > 1.
INDUZIONE
1. BASE INDUTTIVA. S(a) è vera.
2. PASSO INDUTTIVO. S(n-1) implica S(n) vera.
Es.
S(n):
n(n  1)
i  (1  2  ...  n) 

2
i 1
n
Si vuole dimostrare che S(n) vale per ogni n > 1.
1
Base. S(1) è vera perché
 i  1  1(1  1) / 2
i 1
INDUZIONE
1. BASE INDUTTIVA. S(a) è vera.
2. PASSO INDUTTIVO. S(n-1) implica S(n) vera.
Es.
S(n):
n(n  1)
i  (1  2  ...  n) 

2
i 1
n
Si vuole dimostrare che S(n) vale per ogni n > 1.
1
Base. S(1) è vera perché
 i  1  1(1  1) / 2
i 1
Passo. Ipotesi induttiva S(n-1):
n 1
 i  (n  1)n / 2
i 1
INDUZIONE
1. BASE INDUTTIVA. S(a) è vera.
2. PASSO INDUTTIVO. S(n-1) implica S(n) vera.
Es.
S(n):
n(n  1)
i  (1  2  ...  n) 

2
i 1
n
Si vuole dimostrare che S(n) vale per ogni n > 1.
1
Base. S(1) è vera perché
 i  1  1(1  1) / 2
i 1
Passo. Ipotesi induttiva S(n-1):
n 1
 i  (n  1)n / 2
i 1
Si ha
(n  1)n
(n  1)n  2n n(n  1)
i  i  n 
n


2
2
2
i 1
i 1
n
n 1
Quindi S(n) è vera.
INDUZIONE
Esercizio.
Dimostrare per induzione che la seguente affermazione
S(n) è vera per ogni intero n>0.
S(n):
n
i
n 1
2

2
1

i 0
VALIDITA’ delle dimostrazioni per INDUZIONE
Dim. per induzione
Base: S(a) vera
S(n) vera, ogni n>a
Passo induttivo
Minimo controesempio. Supponiamo S(n) falsa per qualche n.
Sia b il più piccolo intero tale che S(b) falsa.
Se b=a contraddiciamo la base. Quindi b>a.
Essendo b-1>a ed avendo scelto b come il minimo intero
per cui l’affermazione è falsa, risulta S(b-1) vera
Per il Passo Induttivo, se S(b-1) è vera allora anche
S(b) è vera.
Abbiamo una contraddizione con l’ipotesi che S(b) è falsa.
Quindi non può esistere un intero per cui l’affermazione
è falsa.
CORRETTEZZA DI PROGRAMMI
Dato un programma (o frammento di programma) si vuole
mostrare che il risultato è quello desiderato.
CORRETTEZZA DI PROGRAMMI
Invariante di ciclo: proprietà vera ad
ogni iterazione; al termine del ciclo
fornisce il risultato desiderato.
CORRETTEZZA DI PROGRAMMI
Invariante di ciclo: proprietà vera ad
ogni iterazione; al termine del ciclo
fornisce il risultato desiderato.
(1) small=i;
(2) for(j=i+1, j<n, j++)
(3)
if (A[j]<A[small]) small=j;
Si vuole mostrare che al termine del
ciclo for la variabile small è tale che
A[small] contiene il min A[i..n-1]
small=i
j=i+1
j<n
Falso, ESCI
vero
(3)
j++
CORRETTEZZA DI PROGRAMMI
Invariante di ciclo: proprietà vera ad
ogni iterazione; al termine del ciclo
fornisce il risultato desiderato.
(1) small=i;
(2) for(j=i+1, j<n, j++)
(3)
if (A[j]<A[small]) small=j;
Si vuole mostrare che al termine del
ciclo for la variabile small è tale che
A[small] contiene il min A[i..n-1]
Invariante di ciclo.
S(k): Se si raggiunge il test “j<n” con
valore di j pari a k allora A[small]
contiene il valore minimo in A[i..k-1].
small=i
j=i+1
j<n
Falso, ESCI
vero
(3)
j++
CORRETTEZZA DI PROGRAMMI
Invariante di ciclo: proprietà vera ad
ogni iterazione; al termine del ciclo
fornisce il risultato desiderato.
(1) small=i;
(2) for(j=i+1, j<n, j++)
(3)
if (A[j]<A[small]) small=j;
Si vuole mostrare che al termine del
ciclo for la variabile small è tale che
A[small] contiene il min A[i..n-1]
Invariante di ciclo.
S(k): Se si raggiunge il test “j<n” con
valore di j pari a k,1<k<n, allora
A[small] contiene il valore minimo in
A[i..k-1].
small=i
j=i+1
j<n
Falso, ESCI
vero
(3)
j++
Si esce dal for con
k=n. => S(n)
CORRETTEZZA DI PROGRAMMI
(1) small=i;
(2) for(j=i+1, j<n, j++)
(3)
if (A[j]<A[small]) small=j;
/* small: indice min A[i..n-1]*/
Invariante di ciclo. S(k): Se si raggiunge il
test “j<n” con valore di j pari a k, 1<k<n,
allora A[small] contiene il min di A[i..k-1].
DIMOSTRAZIONE (per induzione su k).
BASE. k=i+1.
Abbiamo small=i; min A[i..k-1]=min A[i]=A[i].
A[small]=A[i]= min A[i..k-1]. Ok!
small=i
j=i+1
j<n
Falso
vero
(3)
j++
CORRETTEZZA DI PROGRAMMI
(1) small=i;
(2) for(j=i+1, j<n, j++)
(3)
if (A[j]<A[small]) small=j;
/* small: indice min A[i..n-1]*/
Invariante di ciclo. S(k): Se si raggiunge il
test “j<n” con valore di j pari a k, 1<k<n,
allora A[small] contiene il min di A[i..k-1].
PASSO Induttivo. Sia S(k-1) vera.
S(k-1): Se si raggiunge il test “j<n” con
valore di j pari a k-1 allora A[small]
contiene il minimo in A[i..k-2].
Eseguiamo il ciclo con j pari a k-1.
small=i
j=i+1
j<n
Falso
vero
(3)
j++
CORRETTEZZA DI PROGRAMMI
(1) small=i;
(2) for(j=i+1, j<n, j++)
(3)
if (A[j]<A[small]) small=j;
/* small: indice min A[i..n-1]*/
Invariante di ciclo. S(k): Se si raggiunge il
test “j<n” con valore di j pari a k, 1<k<n,
allora A[small] contiene il min A[i..k-1].
PASSO Induttivo. Sia S(k-1) vera.
Eseguiamo il ciclo con j pari a k-1.
Distinguiamo 2 casi:
1) Se A[k-1] > A[small], small invariata
A[small]=min A[i..k-2]=min A[i..k-1]
ok!
small=i
j=i+1
j<n
Falso
vero
(3)
j++
CORRETTEZZA DI PROGRAMMI
(1) small=i;
(2) for(j=i+1, j<n, j++)
(3)
if (A[j]<A[small]) small=j;
/* small: indice min A[i..n-1]*/
2) Se A[k-1] < A[small],
Per ipotesi ind. A[small]=min A[i..k-2]
Quindi A[k-1]< min A[i..k-2]
Otteniamo
A[k-1]=min{A[k-1], min A[i..k-2] }
= min A[i..k-1]
Quando small è posto a k-1,
A[small]=min A[i..k-1].
A questo punto j è incrementato a k
e si ritorna al test con valore di j pari a k e
A[small]=min A[i..k-1].
Quindi S(k) è vera.
OK!
small=i
j=i+1
j<n
Falso
vero
(3)
j++
CORRETTEZZA DI PROGRAMMI
(1) small=i;
(2) for(j=i+1, j<n, j++)
(3)
if (A[j]<A[small]) small=j;
Invariante di ciclo.
S(k): Se si raggiunge il test “j<n” con
valore di j pari a k, i+1<k<n, allora
A[small] contiene il min. di A[i..k-1].
BASE + PASSO Ind.

S(k) vera per ogni k=i+1,…, n.
small=i
j=i+1
j<n
Falso, ESCI
vero
(3)
j++
Correttezza ciclo: si esce dal ciclo quando si raggiunge
il test “j<n” con valore di j pari a n.
L’invariante S(n) per k=n ci dice che
A[small] contiene il min. di A[i..n-1].
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++){
(2) “small=indice min A[i..n-1];
(3)
scambia A[i] ed A[small]; }
i=0
i<n-1
Falso
vero
(2), (3)
i++
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++){
(2) “small=indice min A[i..n-1];
(3)
scambia A[i] ed A[small;}
Si vuole mostrare la Correttezza del ciclo,
cioè che quando si esce dal ciclo l’array
A[0..n-1] è ordinato.
i=0
i<n-1
Falso
vero
(2), (3)
i++
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++){
(2) “small=indice min A[i..n-1];
(3)
scambia A[i] ed A[small;}
Si vuole mostrare la Correttezza del ciclo,
cioè che quando si esce dal ciclo l’array
A[0..n-1] è ordinato.
i=0
i<n-1
vero
(2), (3)
i++
Invariante di ciclo.
T(m): Se si raggiunge il test “i<n-1” con
valore di i pari a m, 0<m<n-1, allora
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
Falso
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++){
(2) “small=indice min A[i..n-1];
(3)
scambia A[i] ed A[small;}
Si vuole mostrare la Correttezza del ciclo,
cioè che quando si esce dal ciclo l’array
A[0..n-1] è ordinato.
i=0
i<n-1
vero
(2), (3)
i++
Invariante di ciclo.
T(m): Se si raggiunge il test “i<n-1” con
valore di i pari a m, 0<m<n-1, allora
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
Falso
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++)
{
(1) “small=indice min A[i..n-1];
(2) scambia A[i] ed A[small;ù
}
Invariante. T(m): Se si raggiunge il
test “i<n-1” con i pari a m, 0<m<n-1,
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
T(n-1) vera  CORRETTEZZA DEL CICLO
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++)
{
(1) “small=indice min A[i..n-1];
(2) scambia A[i] ed A[small;ù
}
Invariante. T(m): Se si raggiunge il
test “i<n-1” con i pari a m, 0<m<n-1,
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
T(n-1) vera  CORRETTEZZA DEL CICLO
Quando si raggiunge il test con i pari a n-1 si esce dal
ciclo.
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++)
{
(1) “small=indice min A[i..n-1];
(2) scambia A[i] ed A[small;ù
}
Invariante. T(m): Se si raggiunge il
test “i<n-1” con i pari a m, 0<m<n-1,
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
T(n-1) vera  CORRETTEZZA DEL CICLO
Quando si raggiunge il test con i pari a n-1 si esce dal
ciclo.
T(n-1) vera  1) A[0..n-2] è ordinato
2) Ogni elemento di A[0..n-2] è < A[n-1].
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++)
{
(1) “small=indice min A[i..n-1];
(2) scambia A[i] ed A[small;ù
}
Invariante. T(m): Se si raggiunge il
test “i<n-1” con i pari a m, 0<m<n-1,
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
T(n-1) vera  CORRETTEZZA DEL CICLO
Quando si raggiunge il test con i pari a n-1 si esce dal
ciclo.
T(n-1) vera  1) A[0..n-2] è ordinato
2) Ogni elemento di A[0..n-2] è < A[n-1].
Quindi A[0..n-1] è ordinato
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++)
{
(1) “small=indice min A[i..n-1];
(2) scambia A[i] ed A[small;ù
}
Invariante. T(m): Se si raggiunge il
test “i<n-1” con i pari a m, 0<m<n-1,
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
Mostriamo per induzione che T(m) vera per ogni m>0.
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++)
{
(1) “small=indice min A[i..n-1];
(2) scambia A[i] ed A[small;ù
}
Invariante. T(m): Se si raggiunge il
test “i<n-1” con i pari a m, 0<m<n-1,
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
BASE. m=0. Array A[0..m-1] è vuoto, niente da provare
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++)
{
(1) “small=indice min A[i..n-1];
(2) scambia A[i] ed A[small];
}
Invariante. T(m): Se si raggiunge il
test “i<n-1” con i pari a m, 0<m<n-1,
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
PASSO.
Ipotesi induttiva (i.i.):T(m) vera. Mostriamo T(m+1) vera.
CORRETTEZZA del SelectionSort
(1) For (i=0,i<n-1,i++)
{
(2) “small=indice min A[i..n-1];
(3) scambia A[i] ed A[small];
}
Invariante. T(m): Se si raggiunge il
test “i<n-1” con i pari a m, 0<m<n-1,
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
PASSO.
Ipotesi induttiva (i.i.):T(m) vera. Mostriamo T(m+1) vera.
Eseguiamo (1) e (2) con i pari a m. Abbiamo
(2)  A[small]=min A[m..n-1]
(3)  A[m]=min A[m..n-1]
CORRETTEZZA del SelectionSort
For (i=0,i<n-1,i++)
{
(2) “small=indice min A[i..n-1];
(3) scambia A[i] ed A[small];
}
Invariante. T(m): Se si raggiunge il
test “i<n-1” con i pari a m, 0<m<n-1,
1) A[0..m-1] è ordinato
2) Ogni elemento di A[0..m-1] è < ogni
elemento di A[m..n-1].
PASSO.
Ipotesi induttiva (i.i.):T(m) vera. Mostriamo T(m+1) vera.
Eseguiamo (2) e (3) con i pari a m. Abbiamo
(2)  A[small]=min A[m..n-1]
(3)  A[m]=min A[m..n-1]
Usando 1) e 2) in i.i. A[0]<A[1]<…<A[m-1]<A[m]
Quindi A[0..m-1] ordinato  1) vale per m.
Inoltre elemento A[m+1..n-1] >
elemento A[0..m-1]
A[m]
Quindi elemento in A[m+1..n-1] > elemento in A[0..m]
 2) vale per m.
CORRETTEZZA CICLI WHILE
Possiamo nuovamente provare la correttezza per induzione
sul numero di volte per cui il ciclo è stato eseguito.
Però può non esistere variabile che conta numero di
esecuzioni.
Inoltre bisogna anche provare che il ciclo termina.
CORRETTEZZA CICLI WHILE
Possiamo nuovamente provare la correttezza per induzione
sul numero di volte per cui il ciclo è stato eseguito.
Però può non esistere variabile che conta numero di
esecuzioni.
Inoltre bisogna anche provare che il ciclo termina.
(1) i=1;
(2) s=0;
(3) while (i<n) {
(4) s=s+i;
(5) i=i+1; }
Si vuole provare che al termine del ciclo la
variabile s contiene la somma dei primi n
interi, cioè 1+2+…+n.
CORRETTEZZA CICLI WHILE
(1) i=1;
(2) s=0;
(3) while (i<n) {
(4) s=s+i;
(5) i=i+1; }
Terminazione. Ad ogni iterazione la variabile i è incrementata di
1, quindi raggiungerà il valore n+1 ed il ciclo termina.
CORRETTEZZA CICLI WHILE
(1) i=1;
(2) s=0;
(3) while (i<n) {
(4) s=s+i;
(5) i=i+1; }
Invariante di cilclo T(j):Se si raggiunge il test “i<n” con i pari a j
allora il valore di s è pari alla somma dei primi j-1 interi.
CORRETTEZZA CICLI WHILE
(1) i=1;
(2) s=0;
(3) while (i<n) {
(4) s=s+i;
(5) i=i+1; }
Invariante di cilclo T(j):Se si raggiunge il test “i<n” con i pari a j
allora il valore di s è pari alla somma dei primi j-1 interi.
Base. j=1. Quando j=1 si ha s=0. Quindi T(0) vera.
CORRETTEZZA CICLI WHILE
(1) i=1;
(2) s=0;
(3) while (i<n) {
(4) s=s+i;
(5) i=i+1; }
Invariante di cilclo T(j):Se si raggiunge il test “i<n” con i pari a j
allora il valore di s è pari alla somma dei primi j-1 interi.
Base. j=1. Quando j=1 si ha s=0. Quindi T(0) vera.
Passo. Assumiamo per i.i. che T(j) vera. Proviamo T(j+1) vera.
Se i vale n+1 si esce dal ciclo, altrimenti iteriamo il ciclo
Eseguendo il ciclo con i pari a j, il valore di s è incrementato di j.
Usando l’i.i.
s vale (1+…+j-1)+j
CORRETTEZZA CICLI WHILE
(1) i=1;
(2) s=0;
(3) while (i<n) {
(4) s=s+i;
(5) i=i+1; }
Invariante di cilclo T(j):Se si raggiunge il test “i<n” con i pari a j
allora il valore di s è pari alla somma dei primi j-1 interi.
Base. j=1. Quando j=1 si ha s=0. Quindi T(0) vera.
Passo. Assumiamo per i.i. che T(j) vera. Proviamo T(j+1) vera.
Se i vale n+1 si esce dal ciclo, altrimenti iteriamo il ciclo
Eseguendo il ciclo con i pari a j, il valore di s è incrementato di j.
Usando l’i.i.
s vale (1+…+j-1)+j
Inoltre i viene incrementata a j+1. Quindi quando si arriva al test
con i pari a j+1 s vale 1+…+j  T(j+1) vera.
CORRETTEZZA CICLI WHILE
(1) i=1;
(2) s=0;
(3) while (i<n) {
(4) s=s+i;
(5) i=i+1; }
Invariante di cilclo T(j):Se si raggiunge il test “i<n” con i pari a j
allora il valore di s è pari alla somma dei primi j-1 interi.
Correttezza.
Usciamo dal ciclo quando eseguiamo il test con i pari a n+1.
T(n+1)  valore di s è pari alla somma dei primi n interi.