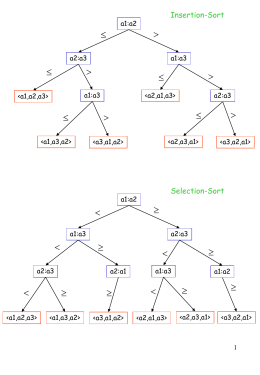
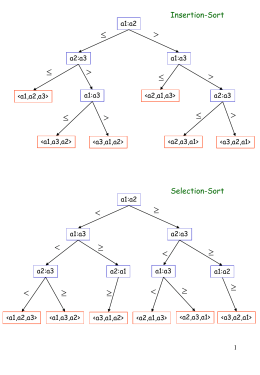
TECNICA
DIVIDE ET IMPERA
Soluzione2: Algoritmo Merge-Sort
05 1
2 28 20 34 47 51 69 73 82 96
05 2 48 50 74 87
25 52 8
25 52
5
2
1 29 3 62 9
6
047
8
04
0
1 39 93
7
4
19
1
26
3
9
2
6
Merge-Sort(A,p,r)
if p < r
q = (p+r)/2
Merge-Sort(A,p,q)
Merge-Sort(A,q+1,r)
Merge(A,p,q,r)
A[p..q]
A[q+1..r]
024578 12369
L
024578
R 12369
01223456789
A[p..r]
Merge(A,p,q,r)
n1 = q – p + 1
n2 = r – q
for i = 1 to n1
L[i] = A[p + i – 1]
for j = 1 to n2
R[j] = A[q + j]
L[n1 + 1] = R[n2 + 1] = 
i=j=1
for k = p to r
if L[i]  R[j]
A[k] = L[i]
i=i+1
else
A[k] = R[j]
j=j+1
Analisi di Merge-Sort: correttezza
Merge-Sort(A,p,r)
A
1
p
non ordinati
r
n
r
n
r
n
if p < r
// altrimenti A[p..r] è ordinato
q = (p+r)/2
Merge-Sort(A,p,q)
Merge-Sort(A,q+1,r)
A
1
p
ordinati
ordinati
q
Merge(A,p,q,r)
A
1
p
ordinati
Merge(A,p,q,r)
A
n1 = q – p + 1
n2 = r – q
for i = 1 to n1
L[i] = A[p + i – 1]
for j = 1 to n2
R[j] = A[q + j]
L[n1 + 1] = R[n2 + 1] = 
A
L
i=j=1
for k = p to r
if L[i]  R[j]
A[k] = L[i]
i=i+1
else
A[k] = R[j]
j=j+1
A
L
1
p
1
p
q
∞
1
n1
p
1
∞
1
A
L
1
1
R
n
r
n
∞
1
n2
r
k
n1
i
r
R
1
p
n
∞
n2
j
rk
∞
n1 i
R
1
n
∞
n2 j
Merge(A,p,q,r) // complessità
n1 = q – p + 1
n2 = r – q
for i = 1 to n1
L[i] = A[p + i – 1]
for j = 1 to n2
R[j] = A[q + j]
L[n1 + 1] = R[n2 + 1] = 
i=j=1
for k = p to r
if L[i]  R[j]
A[k] = L[i]
i=i+1
else
A[k] = R[j]
j=j+1
//
//
//
//
//
//
//
//
//
//
//
//
//
c1
c2
c3
c4 n1  1
c5 n1
c4 n2  1
c5 n2
c6
c7
c8 n  1
c9 n
c10n1
c11n1
// c10n2
// c11n2
T M (n)  (c4  c5  c8  c9  c10  c11 )n
 c1  c2  c3  2c4  c6  c7  c8
 a ' n  b'
n  r  p 1
q  ( p  r ) / 2
n1  n / 2
n2  n / 2
n  n1  n2
Merge-Sort(A,p,r) //complessità
if p < r
q = (p+r)/2
Merge-Sort(A,p,q)
Merge-Sort(A,q+1,r)
Merge(A,p,q,r)
T
MS
//
//
//
//
//
//
c1
c2
c3
T MS n1 
T MS n2 
T M n   a' n  b'
n  r  p 1
n1  q  p  1
n2  r  q
n  n1  n2
se n  1
c1  c2
( n)  
MS
MS
M
c1  c2  c3  T (n1 )  T (n2 )  T (n) se n  1
T
MS
se n  1
c
( n)  
MS
MS
an

b

T
(
n
)

T
(n2 ) se n  1
1

T
log 2 n
MS
se n  1
c
n  
MS
MS
n2  se n  1


T

n
T

b

an
1

T MS n1 
an  b
an1  b
T MS n1,1 
an1,1  b
T MS n1, 2 
an1, 2  b
an  b
T MS n2 
an2  b
T MS n2,1 
an2,1  b
T MS n2,2 
an2, 2  b
c c c c c c c c c c c c
MSMS
TT nn a' nan
loglog
b' nbc('n  1)  cn
2 n 2n
an  2b
an  4b
cn
T MS n  a' n log 2 n  b' n  c'
IS
Tmed
(n)  a" n 2  b" n  c"
T n 
a' n log 2 n  b' n  c'
lim n IS
 lim n
0
2
Tmed n 
a" n  b" n  c"
MS
Dunque esiste N tale che
per ogni n > N.
IS
n 
T MS n   Tmed
Qualunque siano i valori delle costanti a', b', c', a", b" e
c" l’algoritmo Merge-Sort è superiore a Insertion-Sort
per array di dimensione sufficientemente grande.
Possiamo dire che T n  “cresce come” n2
MS
n “cresce come” n log2 n.
T
mentre
IS
MS
n
n2 n log2 n n2 ns n log2 n ns
IS
med
10
100
100 10000
1000 106
10000 108
106 1012
109 1018
33
0.1s
0.033s
664
9965
10s
1ms
0.664s
10s
132877 0.1s
2·107
17m
3·1010 70anni
133s
20ms
30s
T n 
a' n log 2 n  b' n  c'
lim n IS
 lim n

Tmin n 
a" n  b"
MS
IS
n 
dunque esiste N tale che T MS n   Tmin
per ogni n > N.
Qualunque siano i valori delle costanti a', b', c',
a", b" l’algoritmo Insertion-Sort è superiore a
Merge-Sort per array (quasi) ordinati e
sufficientemente grandi.
Insertion-Sort è anche superiore a Merge-Sort per
MS
n
T
array piccoli in quanto le costanti a', b', c' in
sono generalmente molto maggiori delle costanti
IS
T
a", b" e c" in max n  .
Questo suggerisce una modifica di Merge-Sort in
cui le porzioni di array di dimensione minore di
una certa costante k si ordinano con Insertion-Sort
invece di usare ricorsivamente Merge-Sort.
Soluzione3: Algoritmo Merge-Ins-Sort
Merge-Ins-Sort(A,p,r)
if p < r
if r-p+1 < 32
InsertSort(A,p,r)
else
q = (p+r)/2
Merge-Ins-Sort(A,p,q)
Merge-Ins-Sort(A,q+1,r)
Merge(A,p,q,r)