PARABOLA E
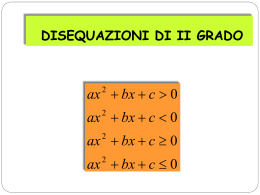
DISEQUAZIONI DI 2° GRADO
Le disequazioni di II grado
Una disequazione intera di II grado può sempre essere
riportata alla forma ax2 + bx + c > 0
 y  ax  bx  c
che a sua volta può essere scritta come 
y0

2
l’interpretazione grafica di tale sistema è la seguente:
determinare i punti della parabola aventi ordinata positiva
Se la disequazione da risolvere è del tipo ax2 + bx + c < 0
si considera invece il sistema
2
 y  ax  bx  c

y0

e perciò si dovrà determinare l’insieme dei punti
della parabola con ordinata negativa
se nella disequazione compare il segno  o  si dovranno
considerare come soluzione anche gli eventuali punti di
intersezione della parabola con l’asse delle x
questi si ottengono risolvendo l’equazione ax2 + bx + c = 0
 b  b  4ac

2a
2
x1/ 2
esempio 1
Risolvere la disequazione x2 - 4  0
y  x  4
Tale disequazione equivale al sistema 
 y0
2
Dobbiamo perciò determinare i punti della parabola y = x2 - 4
che giacciono nel semipiano delle ordinate negative o nulle
Tale parabola ha la concavità rivolta verso l’alto ed
interseca l’asse delle x nei punti A(-2;0) e B(2;0)
y
•A
-2
B•
2


S:[-2;2]
x
esempio 2
Risolvere la disequazione - x2 + 5x + 6 < 0
 y   x  5x  6
Tale disequazione equivale al sistema 
y0

2
Risolviamo la - x2 + 5x + 6 = 0  x =
-1
6
S:]-;-1[]6;[
esempio 3
 y  x2  6x  9

y0

x2 + 6 x +9  0
x2 + 6 x + 9 = 0  x1 = x2 = -3
S = {-3}

esempio 4
3 x2 - x + 1 > 0
 y  3x 2  x  1

y0

3x2 - x + 1 = 0   < 0  non ha radici reali
S=
esempio 5
- x2 + 2 x - 1 > 0
 y  x2  2x 1

y0

- x2 + 2 x - 1 = 0  x1 = x2 = 1
S = {Ø}
esempio 6
- x2 + 8 x - 17  0
 y   x 2  8 x  17

y0

-x2 + 8 x - 17 = 0   < 0  non ha radici reali
S=
=b2-4ac
parabola
>0
(x1 < x2)
x1
x2
valori di x che soddisfano la disequazione
ax2+bx+c>0
ax2+bx+c0
x < x1
x  x1


x > x2
x  x2
qualsiasi
a>0
=0
x1= x2
<0
x con
b
x
2a
x
ax2+bx+c<0
ax2+bx+c0
x1<x<x2 x1 x x2
x
nessun
valore
di x
b
x
2a
x
nessun
valore
di x
nessun
valore
di x
Dall’analisi dello schema si deduce che:
>0
ax2 + bx + c assume lo stesso segno di a per
valori esterni all’intervallo delle radici
=0
ax2 + bx + c assume sempre lo stesso segno
di a escluso i valori per i quali si annulla
<0
ax2 + bx + c assume sempre lo stesso segno di a
trinomio
ax2 + bx +c
-2x2+x+3
2x2+x+1
-x2-2x –1
6x2 + x –2
-x2 +2x – 3
-3x2 +x -2
scrivi
l’equazione
della parabola
corrispondente
y = ax2 + bx +c
y = -2x2+x+3
y= 2x2+x+1
scrivi il
coefficiente del
termine di 2°
grado e indica il
tipo di concavità
della parabola
a =-2
La parabola
volge la
concavità verso
il basso
determina le
intersezioni della
parabola con l’asse
delle x
a=2
La parabola
volge la
concavità verso
l’alto
2x2+x+1 = 0
non ci sono
intersezioni
disegna il grafico
approssimato della
parabola
Scrivi i valori di
x per cui
ax2 + bx +c > 0
Scrivi i valori di
x per cui
ax2 + bx +c < 0
-1 < x < 3/2
x < -1 V x > 3/2
R

-2x2+x+3 = 0
x1 =-1, x2=3/2
disequazione
scrivi
l’equazione
della parabola
corrispondente
al trinomio a
primo membro
scrivi il coefficiente
del termine di 2°
grado e indica il tipo
di concavità della
parabola
a=9>0
La parabola volge la
2
9x2 + 6x + 1  0 y = 9x + 6x +1
concavità verso
l’alto
-2x2 + 3x + 2 >0
9x2+ 6x + 2  0
6x2 -11x + 3  0
-16x2 + 8x –1<0
-5x2 + 2x – 1 <0
9x2 -12x + 4 < 0
determina le
intersezioni della
parabola con l’asse
delle x
9x2 + 6x +1 = 0
x1 = x2=-1/3
disegna il grafico
approssimato della
parabola
Scrivi i valori di x
che verificano la
disequazione
x = -1/3
Esercizi applicativi delle disequazioni di II grado
Risolvere per via algebrica e ricorrendo al grafico della parabola le seguenti disequazioni:
-6x2+7x-20
x2-6x+8>0
4x2+12x+9<0
-x2-6x-9>0
2x2-3x+50
2x2+x+10
Si determini il lato di un quadrato affinché la sua area diminuita di 3 sia maggiore di 6.
Una ditta ha una capacità produttiva massima mensile di kg 1500 di una merce. Per la
produzione sostiene una spesa fissa mensile di lire 500000 ed un costo di lire 1000 per
ogni kg prodotto. La domanda della merce è espressa in funzione del prezzo dalla
relazione x=2400-0,4p dove x è la quantità di merce e p è il prezzo al kg. Calcolare la
quantità di merce che si deve produrre per ottenere il massimo utile, nell’ipotesi che tutta
la quantità prodotta sia venduta.