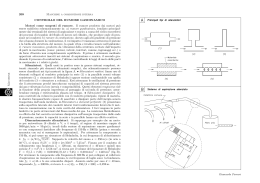
Esercizio n.10
Applicare l’estrapolazione
ricorsiva di Richardson, per
tentare una valutazione numerica
della derivata , nel punto a = 2,
della f(x) sperimentale di cui sono
noti i 17 valori in tabella.
Discutere il risultato.
x
1.000
1.125
1.250
1.375
1.500
1.625
1.750
1.875
2.000
2.125
2.250
2.375
2.500
2.625
2.750
2.875
3.000
f S (x )
1.9656
1.5981
1.4378
1.2409
1.1988
1.1746
1.1187
1.1263
1.0491
1.0512
1.0879
1.0598
0.9994
1.0669
1.0494
1.0543
0.9694
U = 0.0001
Soluzione n.10
Am ,0 
fs(x)
f (a + h)  f (a  h)
;
2h
h
h0
2m
h0  1
2.5
hmin  0.125
2.0
RA  U hmin  0.0008
1.5
Am,k 1  Am1,k 1
4k  1
m  0,1,2, ; k  1,2, , m
1.0
Am,k  Am,k 1 +
0.5
0.0
1.0
k=
1.5
2.5
0
3.0
1
+D/3
D
m
err.
2.0
2
+D/15
3
0
A 00=
-0.4981
1
A 10=
-0.1994
0.2987 A 11=
-0.0998
2
A 20=
-0.0616
0.1378 A 21=
-0.0157
3
A 30=
-0.3004 -0.2388 A 31=
o(h2)
D
3
+D/63
15
0.0842
A 22=
-0.0101
-0.3800 -0.3643
A 32=
-0.4043
o(h4)
o(h6)
D
-0.3942
63
A 33=
-0.4105
o(h8)
Soluzione n.10
Il metodo fornisce una stima (0.4 0.4 !) inaccurata e non convergente a causa del
“rumore” che affligge le misure sperimentali.
La derivata di una funzione in un
punto è molto “sensibile” al
comportamento locale,
nell’intorno del punto, della
funzione stessa. Ciò perchè
fs(x)
2.5
2.0
h
1.5
df S df d

+
dx dx dx
1.0
0.5
e sebbene sia (a)  f(a), in
0.0
1.0
1.5
2.0
2.5
3.0
generale può essere d  df
dx
dx
Si può fare una stima grossolana delle derivate che nel nostro caso, in x = 2, dà:
D 0.1
Df
d
df
0.1


1;


 0.1 ( f è la funzione “regolare” sovrapposta al rumore)
dx
Dx 0.1
dx
Dx
1
Da cui, il “peso” relativo della derivata del
d
rumore su quella totale si può stimare come: dx
df S 
df
 1 +
dx 
dx
1
1
d 
 0.9 del 90% !
 
dx 
1.1
Soluzione n.10
2.5
1 + 1/x^4
fs(x)
noise
2.0
1.5
1.0
Derivata di f (x) = 1 + x 4
funzione sperimentale
privata del rumore.
0.5
0.0
-0.5
1.0
k=
1.5
2.0
0
3.0
1
+D/3
D
m
2.5
2
+D/15
3
D
3
+D/63
15
0
A 00=
-0.4938
1
A 10=
-0.1719
0.3219
A 11=
-0.0646
2
A 20=
-0.1352
0.0367
A 21=
-0.1230
-0.0583
A 22=
-0.1269
3
A 30=
-0.1275
0.0077
A 31=
-0.1249
-0.0019
A 32=
-0.1250
D
0.0018
63
A 33=
-0.1250
Il risultato della stima sarà 0.125  0.002 laddove il risultato esatto è 4/25 = 0.125
Soluzione n.10
Integrale di fS (x) col metodo di Romberg
h0 = 1; Am0=T(h0/2m); RX (b  a)  0.5  U = U = 104
k=
0
1
+D/3
D
3
2
+D/15
15
D
m
0
A 00=
2.5166
1
A 10=
2.3574
-0.1592
A 11=
2.3043
2
A 20=
2.3522
-0.0052
A 21=
2.3504
0.0461
A 22=
2.3535
3
A 30=
2.3476
-0.0046
A 31=
2.3461
-0.0043
A 32=
2.3458
3
+D/63
D
-0.0077
63
A 33=
2.3457
3
Il risultato della stima è 2.346  0.008 laddove

3
1
x 3
4
f ( x )dx  2 +  x dx 2 
 2.3210
1
3 1
3
Il “peso relativo” del rumore nel calcolo dell’integrale si può grossolanamente stimare come
1  ( x)dx  1 +
3


f
(
x
)
dx
1 S

3
1
1 f ( x)dx   1
3

f


(
x
)
dx
1
+
1

3


1
2
1+
0.1
 0.05
Infatti (2.3462.321)/2.346  0.01