Problema del Massimo Flusso
Dati
un grafo orientato G = (N, A) con capacità uij associate agli archi
un nodo s  N, detto sorgente
un nodo t  N, detto pozzo
trovare la massima quantità di flusso che può essere inviata da s a t
rispettando
le capacità degli archi
il fatto che nei nodi intermedi il flusso non può entrare né uscire
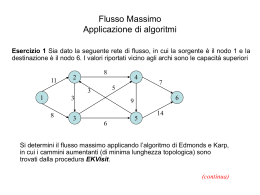
Grafo G :
8
2
4
7
1
4
1
5
6
9
5
3
4
5
sorgente : s = 1
pozzo : t = 6
uij
i
j
Si dice flusso un vettore x  R|A| tale che per ogni nodo intermedio i  N  {s, t}
 j ,i
x  x



 

 BS i
ji
ij
i , j  FS i
i  N \ s,t 
ossia nei nodi intermedi non si ha né immissione né prelievo di flusso
Queste relazioni sono dette “vincoli di conservazione del flusso”
Si dice valore del flusso, denotato con v  R,
la quantità di flusso immessa in rete nel nodo sorgente s
v
x  x


   
 
sj
 s , j  FS s
js
j , s  BS s
Valendo i vincoli di conservazione del flusso ai nodi intermedi,
il flusso immesso in rete nel nodo sorgente s
equivale al flusso prelevato dalla rete nel nodo pozzo t
v
 j ,t
x  x


  

 BS t
jt
tj
t , j  FS t
Il flusso x si dice ammissibile se per ogni arco (i, j)  A
0  xij  uij
 (i, j)  A
Problema del Massimo Flusso :
tra tutti i flussi ammissibili,
determinarne uno cui è associato il massimo valore v
Esempio di flusso ammissibile
xij , uij
i
2, 8
2
4
1, 1
6, 7
4, 4
1
j
1, 5
0, 5
6
5, 9
3
4, 4
5
Il vettore x
è un flusso : soddisfa i vincoli di conservazione del flusso ai nodi
è ammissibile : soddisfa i vincoli di nonnegatività e di capacità
Valore del flusso : v = 6
quantità immessa nella sorgente s e prelevata nel pozzo t
L’arco (i, j) è detto
vuoto se il flusso xij è nullo (coincide con il lower bound)
saturo se il flusso xij è pari alla capacità uij (xij coincide con l’upper bound)
Nell’esempio
l’arco (1, 3) è vuoto
gli archi (2, 3), (3, 5) e (4, 6) sono saturi.
Formulazione PL del problema di Massimo Flusso
Variabili decisionali :
xij : flusso sull’arco (i, j)
v : quantità immessa nel nodo s e prelevata al nodo t (valore del flusso)
Equazioni di conservazione del flusso:
• nodo sorgente : flusso totale pervenuto sugli archi entranti
+ quantità immessa al nodo (deve essere massimizzata)
= flusso totale inviato sugli archi uscenti
x v  x


 
 
 
js
 j , s  BS s
sj
s , j  FS s
• nodo pozzo : flusso totale inviato sugli archi uscenti
+ quantità prelevata al nodo (deve essere massimizzata)
= flusso totale pervenuto sugli archi entranti
 j ,t
x  x v



 

 BS t
jt
tj
t , j  FS t
• nodi di trasferimento  i  s , t :
flusso totale pervenuto sugli archi entranti
= flusso totale inviato sugli archi uscenti
 j ,i
x  x



 

 BS i
ji
ij
i , j  FS i
i  N \ s,t 
vincoli di conservazione del flusso, associati ai nodi del grafo diversi da s e t :
stabiliscono che in ciascun nodo intermedio
il flusso entrante deve essere uguale al flusso uscente,
garantendo l’assenza di dispersioni e di immissioni
Vincoli di nonnegatività e di capacità massima :
0  xij  uij
 (i, j)  A
Funzione obiettivo :  = v
Variabile obiettivo :  (coincide con la variabile decisionale v)
max   v
s.a
x   x  v


 
 
 
js
 j , s  BS s
sj
s , j  FS s
 j ,i
x  x  0



 

 j ,t
x  x  v



 

 BS i
 BS t
ji
jt
ij
i , j  FS i
i  N \ s,t 
tj
t , j  FS t
0  xij  u ij
i, j   A
Modello dell’esempio
max
 v
s.a
 x1, 2  x1,3  v
 x1, 2  x2,3  x2, 4  0
 x1,3  x2,3  x3,5  0
 x2 , 4  x 4 , 5  x4 , 6  0
 x3,5  x4,5  x5, 6  0
 x4, 6  x5, 6  v
Formulazione alternativa del problema di MF
Nella formulazione contenente la variabile decisionale v ,
la matrice dei coefficienti dei vincoli di conservazione del flusso ai nodi
• contiene una colonna in più (la colonna associata alla variabile v)
della matrice di incidenza del grafo G :
gli elementi della colonna associata a v sono
1 nella riga del nodo s
 1 nella riga del nodo t
0 in tutte le altre righe
• può quindi essere interpretata come la matrice di incidenza del grafo G’
ottenuto aggiungendo a G l’arco orientato fittizio (t, s),
detto arco di ritorno, il cui flusso (xts) è rappresentato dalla variabile v.
Grafo G’ :
8
2
4
7
1
4
1
5
9
5
3
sorgente : s = 1
pozzo : t = 6
6
4
5
Si introduce un arco fittizio di ritorno (t, s) con capacità uts = M,
con M valore opportunamente grande
tale che M sia maggiore del valore della soluzione ottima.
max xts
i, j  A'
0  xij  uij
x

 
 j ,i BS
ji
i
dove A’ = A  {(t,s)}

x 0

 
ij
i , j FS i
iN
Il problema che in G è un problema di MF,
su G’ è un problema di circolazione (caso particolare di MCF) :
• vettore b dei bilanci è nullo (bi = 0,  i) :
tutti i nodi, compresi s e t, sono di trasferimento
(nella rete non c’è immissione o prelievo, ma solo circolazione)
• vettore c dei costi è nullo, tranne che per l’arco fittizio (t, s),
in cui è 1 (cts = 1, cij = 0  (i, j)  (t, s)) :
(la minimizzazione di v corrisponde alla massimizzazione
del valore v del flusso che transita lungo l’arco (t, s),
ossia del flusso inviato, nel grafo originario G, da s a t)
In generale :
• se dal grafo G, su cui è definito il problema di Massimo Flusso,
si ottiene il grafo G’ aggiungendo l’arco fittizio (t, s)
• se in G’ si pongono a 0 i deficit dei nodi s e t
• se in G’ si definiscono i costi di percorrenza degli archi
cts = –1 per l’arco (t, s) , cij = 0 per tutti gli altri archi
si ottiene un problema (MCF) di circolazione in cui
il flusso totale v sui grafi G e G’ è il flusso dell’arco (t, s) di G’
Nell’esempio, il valore del flusso : v = 6
pari al numero di unità uscenti dalla sorgente s ed entranti nel pozzo t
(nel corrispondente problema di circolazione sul grafo G’
è il valore di xts, flusso sull’arco di ritorno)
Esempio di problema di massimo flusso
Sono dati
• un’officina meccanica con M operai (con identiche capacità lavorative)
• un insieme J = {1,…, n} di macchine da riparare
Ogni macchina da riparare j è caratterizzata dalla terna (pj , rj , dj), dove
pj : tempo necessario per ripararla
rj : ora in cui il proprietario la consegna all’officina
dj : ora in cui la macchina viene ritirata
Le riparazioni
possono venire interrotte e riprese (prelazione) senza perdite di tempo
devono essere eseguite da un operaio alla volta
Problema :
trovare un assegnamento delle riparazioni agli operai
in modo da consegnare le macchine entro l’orario stabilito
Il problema può essere risolto per mezzo della ricerca
di un flusso massimo su un opportuno grafo.
Esempio :
M = 3 (n° operai)
i dati relativi ai lavori in J sono riportati dalla seguente tabella
Ordiniamo gli “eventi” (consegne o ritiri di macchine) in ordine crescente
(eliminando le ripetizioni) : 1, 3, 4, 5, 7, 9
Tra due “eventi” consecutivi abbiamo intervalli di tempo di lavoro continuato (Tkl):
T13(2 ore), T34(1 ora), T45(1 ora), T57(2 ore), T79(2 ore)
Durante l’intervallo Tkl possono venir riparate le macchine
che sono arrivate prima di k (rj < k) e vengono ritirate dopo l (dj > l).
Costruzione del grafo
Insieme dei nodi
nodo sorgente s
nodo pozzo t
un nodo per ogni macchina j  J
un nodo per ogni intervallo Tkl
Insieme degli archi, con rispettive capacità
• il nodo sorgente s è collegato ad ogni nodo-macchina j  J
con un arco di capacità uguale al tempo di riparazione pj
• ogni nodo-macchina j  J è collegato ad ogni nodo-intervallo Tkl
nel quale la macchina può essere riparata,
con un arco di capacità (lk)
• ogni nodo-intervallo Tkl è collegato al pozzo t,
con un arco di capacità pari alla capacità lavorativa dell’officina
in tale intervallo cioè M·(lk)
2
1
3
2
1
r2
3
r1
r3
1
3
3
4
4
4 5
d 2 r4
d1
7
d3
9
d4
pj
l k
1
2
8.45 ore di lavoro richieste
(1 centesimo di ora = 36”)
1.25
s
2.10
1
3
3.60
T45
1
2
3
3
t
6
T57
2
4
Le ore di consegna e ritiro dei lavori
sono compatibili con la distribuzione
nel tempo delle ore disponibili ?
T34
1
2
M·(l k)
6
1
1
1.50
T13
6
2
T79
24 ore di lavoro
disponibile
(8 ore  3 operai)
max
v
s.a  xs ,1  xs , 2  xs ,3  xs , 4  v
xs ,1  x1,T34  x1,T45  0
xs , 2  x2,T13  x2,T34  0
xs ,3  x3,T34  x3,T45  x3,T57  0
xs , 4  x4,T57  x4,T79  0
x2,T13  xT13 ,t  0
x1,T34  x2,T34  x3,T34  xT34 ,t  0
x1,T45  x3,T45  xT45 ,t  0
x3,T57  x4,T57  xT57 ,t  0
x4,T79  xT79 ,t  0
xT13 ,t  xT34 ,t  xT45 ,t  xT57 ,t  xT79 ,t  v
0  xs ,1  1.5
0  xs , 2  1.25
0  xs ,3  2.1
0  xs , 4  3.6
0  x1,T3 4  1
0  x1,T4 5  1
0  x2,T1 3  2
0  x2,T3 4  1
0  x3,T3 4  1
0  x3,T4 5  1
0  x3,T5 7  2
0  x4,T5 7  2
0  x4,T7 9  2
0  xT1 3 ,t
0  xT3 4 ,t
0  xT4 5 ,t
0  xT5 7 ,t
0  xT7 9 ,t
6
3
3
6
6
Soluzione del problema
v  8.45
x s ,1  1.5
x s , 2  1.25
x s ,3  2.1
x s , 4  3.6
x1,T34
x1,T45
x 2,T13
x 2,T34
x3,T34
x3,T45
x 4,T57
x 4,T57
x 4,T79
1
 0.5
 0.25
1
 0.1
0
2
2
 1.6
xT13 ,t
xT34 ,t
xT45 ,t
xT57 ,t
xT79 ,t
 0.25
 2.1
 0.5
4
 1.6
2
1
3
2
1
r2
3
r1
r3
pj
l k
1.5
1.5
1, 1
1
0.5, 1
0.25, 2
1, 1
2
0.1, 1
1.25
s 1.25
2.1
2.1
3.6
3.6
3
4
3
4
1
3
4 5
d 2 r4
d1
0, 1
2, 2
2, 2
1.6, 2
4
7
d3
9
d4
M·(l k)
T13
0.25, 6
T34
T45
2.10, 3
0.50, 3
t
4, 6
T57
1.60, 6
T79
Il flusso sugli archi del grafo così costruito
rappresenta la quantità di lavoro che viene svolto.
Se il flusso massimo che si può spedire da s a t
è uguale alla somma dei tempi di riparazione
(= capacità degli archi uscenti da s),
allora è possibile riparare tutte le macchine entro i tempi stabiliti.
v, valore del flusso x : quantità immessa nel nodo s e prelevata al nodo t
v
x  x


   
 
sj
 s , j  FS s
js
j , s  BS s
2, 8
2
4
1, 1
6, 7
4, 4
1
1, 5
0, 5
5, 9
3
Ns = { s }
6
4, 4
5
Nt = { 2, 3, 4, 5, t }
v
 j ,t
x  x



 

 BS t
jt
tj
t , j  FS t
2, 8
2
4
1, 1
6, 7
4, 4
1
1, 5
0, 5
6
5, 9
3
4, 4
Ns = { s, 2, 3, 4, 5 }
5
Nt = { t }
Proprietà di flussi e tagli
Taglio s-t del grafo G :
partizione dell’insieme N dei nodi in due sottoinsiemi (Ns , Nt) con
s  Ns
e
t  Nt = N \ Ns
Gli archi che attraversano il taglio (che hanno un estremo in Ns e l’altro in Nt)
sono a loro volta distinti in due sottoinsiemi:
• l’insieme A+(Ns, Nt) degli archi diretti del taglio
(uscenti da un nodo di Ns ed entranti in un nodo di Nt)
A+(Ns, Nt) = {(i, j)  A : i  Ns , j  Nt }
• l’insieme A–(Ns, Nt) degli archi inversi del taglio
(uscenti da un nodo di Nt ed entranti in un nodo di Ns)
A–(Ns, Nt) = {(i, j)  A : i  Nt , j  Ns }
Dato un flusso x, ad ogni taglio s-t è associato il flusso del taglio
dato dalla quantità di flusso che percorre gli archi diretti
meno la quantità di flusso che percorre gli archi inversi
e denotato col simbolo x(Ns, Nt))
x N s , N t  
x
ij

i , j   A  N s , N t 

x
ij
i , j   A  N s , N t 

(valore netto tra quanto fluisce verso t e quanto ritorna verso s)
Ad ogni taglio s-t del grafo G è associata la capacità del taglio
data dalla somma delle capacità degli archi diretti
e denotata col simbolo u(Ns, Nt) :
u N s , N t  
u
ij
i , j   A  N s , N t 

Teorema
 x , flusso ammissibile di valore v
 (Ns, Nt), taglio s-t del grafo G,
a)
x(Ns, Nt) = v
b)
x(Ns, Nt)  u(Ns, Nt)
ossia, il flusso x(Ns, Nt) del taglio (Ns, Nt)
• coincide con il valore v del flusso x
• non supera la capacità u(Ns, Nt) del taglio
Dimostrazione di a)
Sommando membro a membro
le equazioni di conservazione del flusso relative ai nodi dell’insieme Nt
 j ,i
x  x 0


  

 j ,t
x  x v


  

 BS i
 BS t
ji
jt
ij
i , j  FS i
tj
t , j  FS t
si ottiene



v
x

x



ji
ij


iN t   j , i  BS i 
i , j FS i  
i  N t \  t 
Nella sommatoria sugli archi (j, i)  BS(i) :
• se j  Ns : (j, i) è arco diretto del taglio ((j, i)  A+(Ns, Nt))
• se j  Nt : l’arco (j, i) ha entrambi gli estremi in Nt
Nella sommatoria sugli archi (i, j)  FS(i) :
• se j  Ns : (i, j) è arco inverso del taglio ((i, j)  A–(Ns, Nt))
• se j  Nt : l’arco (i, j) ha entrambi gli estremi in Nt
Gli archi con entrambi gli estremi j e i in Nt si elidono perché compaiono
con coefficiente +1 nella sommatoria sugli archi (j, i)  BS(i)
con coefficiente –1 nella sommatoria sugli archi (i, j)  FS(i)
Quindi a secondo membro resta la differenza tra la somma dei flussi sugli
archi diretti e la somma dei flussi degli archi inversi (flusso del taglio)
v
x
ji
 j ,i A  N s ,Nt 

x
ij
i , j A  N s ,Nt 
 x N s , N t 
Dimostrazione di b)
Sommando membro a membro
1.
i vincoli di capacità per gli archi diretti del taglio
2.
i vincoli di nonnegatività per gli archi inversi del taglio
si ottengono rispettivamente le seguenti relazioni
1.
2.
x

x
0
ij

i , j A  N s , N t 
ij

i , j A  N s , N t 
ij
i , j A  N s , N t 

dalle quali segue
ossia
u
x
ij

i , j A  N s , N t 
x N s , N t   u  N s , N t 

x
ij

i , j A  N s , N t 

u
ij
i , j A  N s , N t 

Condizioni di ottimalità per MF
Siano
x : flusso ammissibile
v : valore del flusso x
Il flusso ammissibile x non è ottimo
se riusciamo ad inviare altro flusso dall’origine s alla destinazione t.
Tale flusso aggiuntivo è “instradato” lungo un cammino P da s a t.
Esempio 1 :
2, 8
2
4
1, 1
6, 7
4, 4
1
1, 5
0, 5
6
5, 9
3
4, 4
5
cammino P su cui inviare nuovo flusso da s a t
P = { (1, 2), (2, 4), (4, 5), (5, 6) }
capacità  del cammino P dato il flusso x :
 (P, x) = min { 7  6, 8  2, 5  1, 9  5 } = 1
Si ottiene il nuovo flusso ammissibile
3, 8
2
4
1, 1
7, 7
4, 4
1
2, 5
0, 5
6
6, 9
3
4, 4
5
v=7
Esempio 2 :
2, 8
2
4
1, 1
6, 7
4, 4
1
1, 5
0, 5
6
5, 9
3
4, 4
5
cammino P su cui inviare nuovo flusso da s a t
P = { (1, 3), (2, 3), (2, 4), (4, 5), (5, 6) }
capacità  del cammino P dato il flusso x :
 (P, x) = min { 5  0, 4, 8  2, 5  1, 9  5 } = 4
Si ottiene il nuovo flusso ammissibile
6, 8
2
4
1, 1
6, 7
0, 4
1
5, 5
4, 5
6
v = 10
9, 9
3
4, 4
5
Effettuati contemporaneamente
redistribuzione su percorsi diversi del flusso già presente sulla rete
invio di 4 unità di flusso aggiuntivo
Un cammino P su cui sia possibile inviare nuovo flusso è detto
cammino aumentante.
I cammini aumentanti non sono necessariamente orientati :
possono essere composti
• sia da archi che vengono attraversati nel verso del loro orientamento
(archi concordi)
• sia da archi che vengono attraversati nel verso opposto
(archi discordi)
P+ : insieme degli archi concordi del cammino P
P– : insieme degli archi discordi del cammino P
Capacità  (P, x) del cammino aumentante P rispetto al flusso x :
 (P, x) = min { min{uij – xij : (i, j)  P+} , min{xij : (i, j)  P–} }
È la massima quantità di flusso che
• aggiunta agli archi concordi di P non produce flussi maggiori delle capacità
• sottratta agli archi discordi di P non produce flussi negativi
 (P, x) = 0 , se almeno uno degli archi concordi è saturo (xij = uij)
oalmeno uno degli archi discordi è vuoto (xij = 0)
 (P, x) > 0 : il cammino è detto AUMENTANTE
Se x è un flusso, ossia soddisfa i vincoli di conservazione del flusso,
per ogni scalare reale , il vettore x() = x  P,
definito, componente per componente, dall’operazione di composizione
 xij  

xij     xij  
x
 ij
se i, j   P 
se i, j   P 
altrimenti
soddisfa i vincoli di conservazione del flusso (è quindi un flusso)
e il valore del flusso x() è v + .
Se  =  , con  capacità del cammino aumentante P rispetto al flusso x,
x( ) = x   P soddisfa anche i vincoli di nonnegatività e di capacità :
x( ) è flusso ammissibile.
Determinazione di un cammino aumentante P
rispetto al flusso ammissibile x su un grafo G :
si introduce il grafo residuo Gx = ( N, Ax ) rispetto al flusso x, dove
Ax   i, j  : i, j   A, xij  uij  
  j, i  : i, j  A,
ossia
 un arco (i, j) non saturo e non vuoto in G (0 < xij < uij)
è rappresentato in Gx da una coppia di archi
• un arco (i, j) di capacità uij – xij
• un arco (j, i) di capacità xij
 un arco (i, j) vuoto (xij = 0) [ saturo (xij = uij) ] in G
è rappresentato in Gx da un arco (i, j) [(j, i)] di capacità uij
xij  0
Lemma:
per ogni cammino aumentante da s a t rispetto a x in G
esiste uno ed un solo cammino orientato da s a t in Gx
Mediante il grafo residuo Gx , il concetto di cammini aumentanti
è ricondotto al più usuale concetto di cammini orientati :
archi di Gx associati ad archi non saturi [non vuoti] di G
sono candidati ad appartenere all’insieme P+ degli archi concordi
[all’insieme P– degli archi discordi] di un cammino aumentante
Un cammino aumentante può essere determinato
mediante una visita del grafo residuo Gx a partire da s :
possono presentarsi 2 casi
• la visita raggiunge t :
risulta individuato un cammino aumentante
che permette di costruire un nuovo flusso x’
di valore strettamente maggiore al valore di x :
si è ottenuta, per costruzione, una prova della non ottimalità di x
• la visita non raggiunge t :
su N, insieme dei nodi di G, si definisce la partizione ( Ns, Nt ) :
Ns : sottoinsieme dei nodi raggiunti dalla visita (contiene s)
Nt : sottoinsieme dei nodi non raggiunti dalla visita (contiene t)
Quando la visita del grafo residuo Gx non raggiunge il nodo t,
il taglio s-t definito dalla partizione (Ns, Nt) con
Ns : insieme dei nodi visitati a partire da s
Nt = N \ Ns: insieme dei nodi non visitati
è tale che v = u(Ns, Nt)
In tale taglio s-t, infatti
• tutti gli archi di A+ (Ns, Nt) sono saturi
• tutti gli archi di A– (Ns, Nt) sono vuoti
altrimenti l’algoritmo avrebbe potuto visitare un ulteriore nodo
Quindi, dalle definizioni di flusso del taglio e di capacità del taglio,
v  x N s , N t  
x
ij

i , j A  N s , N t 



i , j A  N s , N t 
uij
perché tutti
gli archi diretti
sono saturi

u
ij

i , j A  N s , N t 

x
ij

i , j A  N s , N t 


0
perché tutti
gli archi inversi
sono vuoti
 u N s , N t 
segue anche che (Ns, Nt) deve necessariamente essere
un taglio di capacità minima tra tutti i tagli del grafo che separano s da t
Essendo v = x(Ns, Nt) = u(Ns, Nt),
non può esistere un taglio (Ns’, Nt’) del grafo
di capacità u’(Ns’, Nt’) strettamente minore di u(Ns, Nt) :
infatti, se un tale taglio esistesse, si avrebbe u’(Ns’, Nt’) < x(Ns, Nt) = v :
ciò sarebbe in contraddizione con u(Ns, Nt)  x(Ns, Nt) (Ns, Nt)
(e quindi anche per la partizione (Ns’, Nt’) )
Abbiamo dimostrato che
il massimo valore dei flussi ammissibili su G
è uguale
alla minima capacità dei tagli di G che separano s da t
Teorema del Flusso Massimo e del Taglio Minimo o Max flow – Min cut
Algoritmo dei cammini aumentanti o di Ford-Fulkerson
Procedure Cammini-Aumentanti (G, s, t, x, Ns, Nt) :
begin
x := 0 ;
while Trova-Cammino(G, s, t, x, P, , Ns, Nt) do
Aumenta-Flusso(x, P, )
end.
 Inizializzazione : flusso nullo
 Procedura Trova-Cammino :
cerca di determinare un cammino aumentante P da s a t, dato il flusso x :
• è una visita del grafo residuo Gx a partire dall’origine s
• insieme a P determina la capacità  =  (P, x) di P
memorizzando, per ciascun nodo j raggiunto nella visita,
la capacità dj dell’unico cammino da s a j
sull’albero Ts = (Ns, As) determinato fino a quel momento;
Avendo ad es. inizializzato la procedura con ds = nil ,
quando si giunge al nodo j provenendo dal nodo i:
• se si è usato l’arco (i, j):
dj = min { di , uij – xij }
• se si è usato l’arco (j, i):
dj = min { di , xji }
confronto tra
capacità del cammino s-i e
capacità residua dell’arco (i, j))
confronto tra
capacità del cammino s-i e
flusso dell’arco (i, j))
• se il cammino esiste:
la procedura Trova-Cammino restituisce vero
e fornisce P e  =  (P, x))
• se il cammino non esiste:
la procedura restituisce falso
e fornisce un taglio s-t di capacità minima,
che certifica l’ottimalità del flusso
Procedura Aumenta-Flusso
• aggiorna il flusso x inviando sul cammino P la quantità di flusso ,
ossia implementa l’operazione di composizione x() = x  P
• ciò è fatto percorrendo il cammino in senso inverso da t a s,
per mezzo della funzione predecessore, e modificando il flusso
 xij  θ se i, j   P 

xij θ    xij  θ se i, j   P 
x
altrimenti
 ij
La funzione predecessore della procedura di visita standard
non distingue l’orientamento degli archi del grafo originale:
pj = i non indica se per andare dal nodo i al nodo j
si è usato l’arco (i, j) (percorrendolo secondo il suo orientamento)
oppure l’arco (j, i) (percorrendolo nel verso opposto al suo orientamento)
Nella Trova-Cammino porre
• pj = i : se j viene visitato a partire da i mediante l’arco (i, j)
• pj = – i : se j viene visitato mediante l’arco (j, i).
Flusso massimo con più sorgenti/pozzi
Dati
• un insieme S di nodi sorgente
• un insieme T di nodi pozzo
Individuare il massimo flusso che può essere inviato dai nodi sorgente ai nodi pozzo.
Risoluzione 1 (si modifica il grafo e non l’algoritmo):
applicare un algoritmo per MF al grafo ampliato G’ = (N’, A’) con
•
N’ = N  {s, t}
s e t sono la “super-sorgente” ed il “super-pozzo”
•
A’ = A  { (s, j) : j  S}  {(i, t) : i  T }
gli archi che collegano la “super-sorgente” a tutti i nodi in S
ed il “super-pozzo” a tutti i nodi in T hanno capacità infinita
Risoluzione 2 (si modifica l’algoritmo e non il grafo):
la procedura Trova-Cammino implementa una visita
a partire dall’insieme di nodi S invece che dal singolo nodo s (inizializza Q = S)
La visita è interrotta in uno dei seguenti due casi :
•
si raggiunge un qualsiasi nodo in T :
si è determinato un cammino aumentante
da una delle sorgenti ad uno dei pozzi
•
Q è vuoto :
si è determinato un taglio saturo, ossia flusso = capacità,
che separa tutte le sorgenti da tutti i pozzi
2) Flusso massimo con più sorgenti i  S e pozzi i  T
aventi capacità finita ui,
ossia una massima quantità di flusso
che può essere immessa nella o prelevata dalla rete
Risoluzione 1 (si modifica il grafo e non l’algoritmo):
applicare un algoritmo per MF al grafo ampliato G’ = (N’, A’)
dove la capacità degli archi (s, i) e (i, t) viene posta a ui e non a + 